Что такой луч в математике

Луч в математике — это прямая линия, которая имеет начальную точку и простирается бесконечно в одном направлении. Узнайте, как определяется луч и какие свойства он имеет в математике.

В математике луч – это одно из основных понятий, которое используется для описания прямых линий и их отрезков. Луч можно представить себе как бесконечно длинную линию, которая начинается в определенной точке и продолжается бесконечно в одном направлении. Он отличается от отрезка тем, что у него нет конца и он не ограничен каким-либо отрезком.

Определение луча в математике имеет важное значение в геометрии, алгебре и других областях науки. Лучи используются для моделирования различных физических и геометрических объектов, а также для решения задач в аналитической геометрии и алгебре. Понимание этого понятия позволяет более точно описывать и анализировать геометрические формы и объекты.

Примером луча может служить солнечный луч, который начинается в Солнце и продолжается в бесконечность. Также луч можно представить себе как линию, которая начинается в одной точке и расширяется в одном направлении, например, луч света, который идет от источника света.

Определение луча

Луч можно представить как стрелку, которая начинается в точке и указывает в одном направлении. Луч не имеет конца, поэтому он продолжается в бесконечности.

Математически луч может быть обозначен стрелкой над двумя буквами, где первая буква обозначает точку начала, а вторая — направление луча. Так, луч, начинающийся в точке A и направленный вправо, может быть обозначен как AB.

Лучы используются в математике и геометрии для определения линейных объектов и отношений, а также для решения различных задач и заданий.

Примеры лучей в реальной жизни включают лучи солнца, лучи света от фар автомобилей и лучи лазера.

Луч как геометрическая фигура

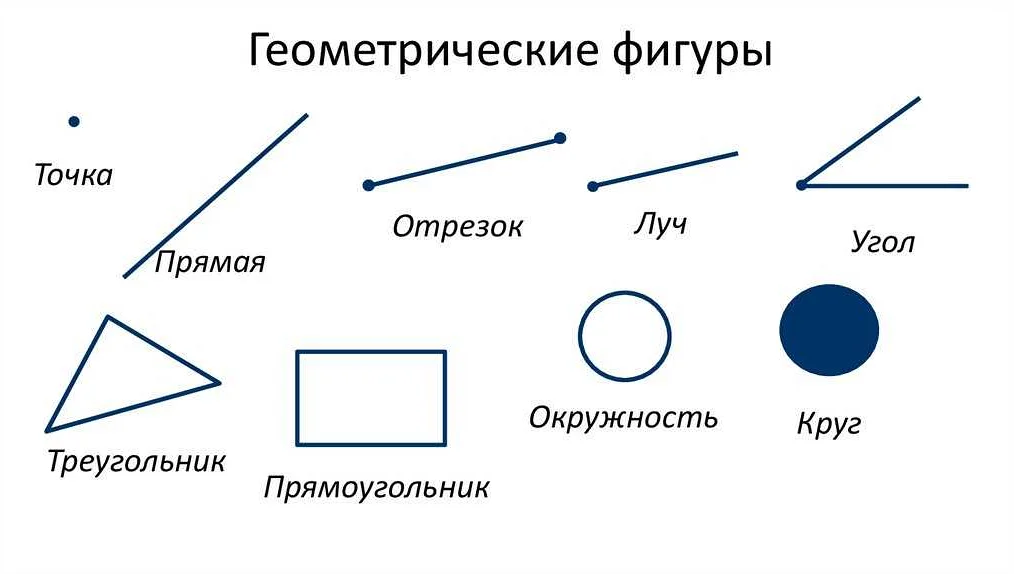
Основные элементы луча:

1. Начальная точка: точка, с которой начинается луч и обозначается обычно буквой «A».
2. Направление: направление, в котором простирается луч, обозначается стрелкой, указывающей вдоль луча.
3. Бесконечность: луч простирается бесконечно в одном направлении и не имеет конечной точки.

Луч может быть обозначен с помощью двух точек. Начальная точка обозначается первой буквой, а направление указывается стрелкой, указывающей на вторую точку. Например, луч AB может быть обозначен как луч, начинающийся в точке A и направленный в точку B.

Луч используется в различных областях математики и геометрии, например, при построении графиков функций, а также для определения углов, отрезков и других геометрических фигур.

Определение направленного луча

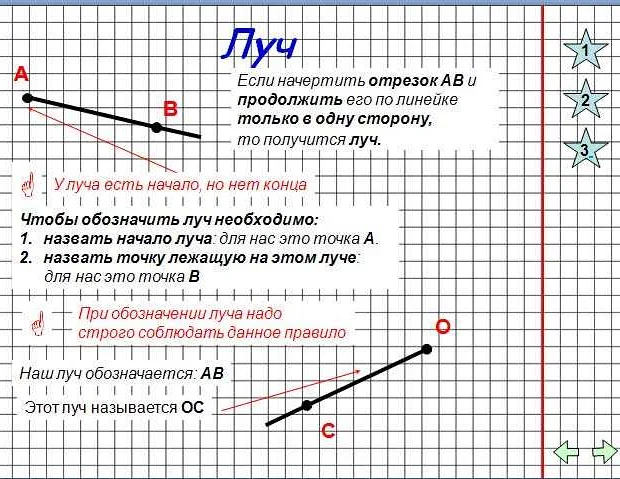
Направленный луч в математике представляет собой участок прямой, начинающийся в определенной точке и продолжающийся в бесконечность в одном направлении.

Направленный луч обозначается с помощью двух букв, причем первая буква указывает на начальную точку, а стрелка указывает направление продолжения луча.

Направленный луч AB можно записать как AB → или так: A → B.

Направленный луч CD можно записать как CD → или так: C → D.

Важно понимать, что направленный луч не имеет конца и продолжается в одном направлении бесконечно.

Например, если мы имеем направленный луч AB, начинающийся в точке A и направленный в сторону точки B, то мы можем продолжать рисовать линию в этом направлении, бесконечно удаляясь от точки A.

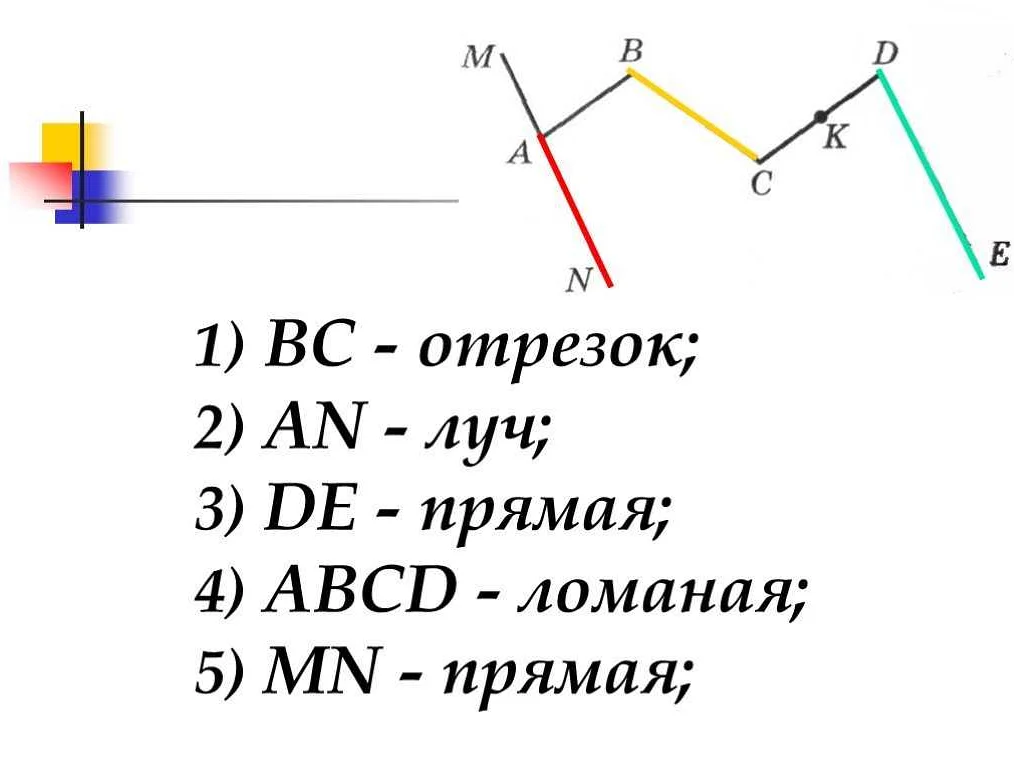
Примеры использования лучей в геометрии

Лучи в геометрии используются для решения различных задач и построения геометрических фигур. Рассмотрим несколько примеров использования лучей:

1. Построение отрезка

Для построения отрезка можно использовать два луча. Первый луч начинается в точке A и направлен в точку B, а второй луч начинается в точке B и направлен в точку A. Место пересечения этих двух лучей будет являться серединой отрезка AB.

2. Определение угла

Лучи также используются для определения углов. Для этого можно взять два луча, один из которых начинается в вершине угла, а второй луч проходит через две стороны угла. Место пересечения этих двух лучей будет являться вершиной угла.

3. Построение прямой

При построении прямой можно использовать два луча. Один луч начинается в точке A и направлен вправо, а второй луч начинается в точке A и направлен влево. Место пересечения этих двух лучей будет являться началом прямой, а прямая будет проходить через все точки, лежащие на лучах.

Таким образом, использование лучей в геометрии позволяет решать различные задачи и строить геометрические фигуры.

Абстрактное понятие луча

Луч может быть описан с помощью двух точек. Одна из точек является началом луча, а другая точка может быть любой точкой, лежащей на линии луча или за пределами его. Обычно луч обозначается двумя буквами, где первая буква обозначает начало луча, а вторая буква — любую другую точку, лежащую на линии луча.

Например, если луч обозначается как AB, где A — начало луча, а B — любая точка на луче, то можно сказать, что луч AB распространяется от точки A в бесконечность в направлении точки B.

Луч — это важное понятие в геометрии и может быть использован для определения углов, прямых и других геометрических фигур. Он также играет важную роль в различных областях математики, физики и инженерии.

Видео по теме:

Вопрос-ответ:

Что такое луч в математике?

В математике луч — это прямая линия, которая начинается в одной точке и стремится к бесконечности в одном направлении.

Как определить направление луча?

Направление луча определяется стрелкой на конце луча. Она указывает, куда будет продолжаться луч в бесконечности.

Как обозначают лучи в математике?

Лучи обычно обозначаются двумя буквами, например, AB. Буква A указывает на начало луча, а Буква B может быть любой, так как луч продолжается в одном направлении.

Какие бывают примеры лучей в математике?

Примерами лучей могут быть: отрезок прямой дороги, линия солнечных лучей, прямая линия, идущая вдоль замерзшей реки.

Как использовать лучи в решении задач в математике?

Лучи могут использоваться для визуализации и описания направления движения, расположения или распространения объектов в задачах, связанных с геометрией или физикой.

Что такое луч в математике?

Луч в математике — это геометрический объект, который представляет собой прямую линию, начинающуюся в одной точке и простирающуюся бесконечно в одном направлении. Он имеет только одну границу — начальную точку, которая называется началом луча. Луч можно представить как половину прямой.

Какие бывают примеры лучей в математике?

Примеры лучей в математике могут быть разнообразными. Например, луч может быть вертикальным или горизонтальным, направленным вверх или вниз. Также луч может быть наклонным под определенным углом. Например, можно представить луч, начинающийся в точке (0,0) и направленный вверх, или луч, начинающийся в точке (2,5) и направленный вниз и вправо. В общем случае, луч может быть представлен в виде уравнения вида y = mx + b, где m — наклон луча, b — смещение от начала координат.

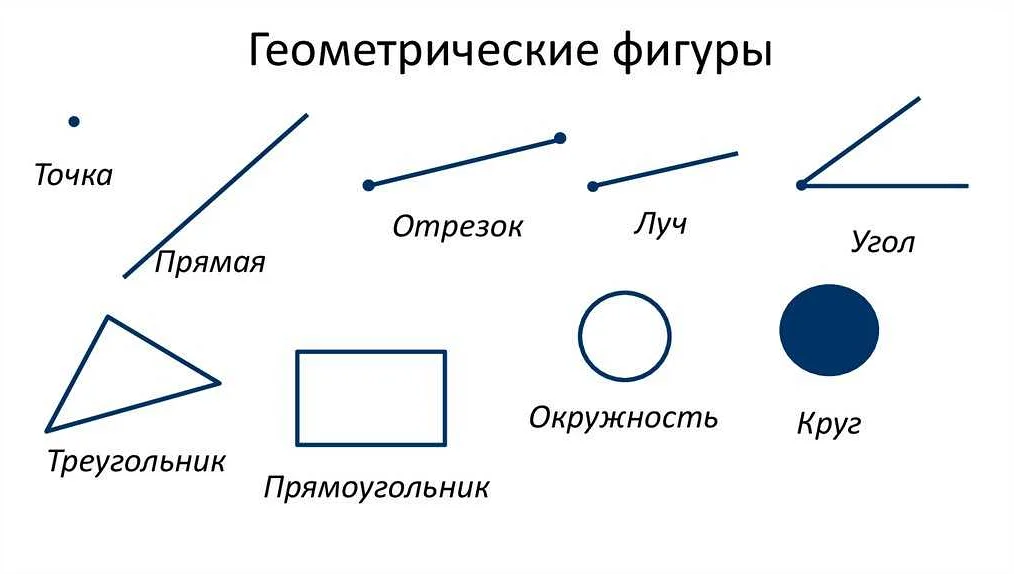
Свойства лучей

Свойство	Описание
1	Луч имеет только одно начало, но продолжается бесконечно в одном направлении.
2	Два луча с общей начальной точкой называются противоположными, если они продолжаются в противоположных направлениях.
3	Лучи, которые не пересекаются и не являются параллельными, образуют плоский угол. Угол образуется двумя лучами с общей начальной точкой.
4	Если луч пересекает прямую, то он делит ее на две части: положительную и отрицательную.
5	Лучи, которые имеют общую начальную точку и лежат на одной прямой, называются коллинеарными лучами.

Эти свойства лучей являются основными для понимания и работы с лучами в математике.

Применение лучей в решении задач

Лучи в математике используются для решения различных задач и проблем. Их применение позволяет наглядно представить и описать различные ситуации и ограничения.

Одним из основных применений лучей является решение геометрических задач. Лучи могут быть использованы для определения направления и расстояния между точками, а также для построения различных фигур и объектов.

Например, при решении задач о нахождении пересечений, лучи могут быть использованы для определения места пересечения двух линий или отрезков. Также лучи могут помочь в определении взаимного расположения различных объектов, например, при определении принадлежности точки заданному отрезку.

Лучи также широко применяются при решении задач о зрении и оптике. Например, лучи света могут быть использованы для определения пути света в оптической системе, а также для определения фокусного расстояния линзы или зеркала.

Кроме того, лучи могут быть использованы для решения задач в физике и механике. Например, лучи могут быть использованы для определения направления движения объекта или для описания преломления света в различных средах.

В целом, применение лучей в решении задач позволяет упростить и наглядно представить различные математические и физические концепции. Они являются важным инструментом для анализа и решения задач в различных областях науки и техники.