Что значит построить математическую модель задачи
Содержимое
- 1 Что значит построить математическую модель задачи
- 1.1 Что такое математическая модель
- 1.2 Видео по теме:
- 1.3 Зачем нужна математическая модель
- 1.4 Построение математической модели
- 1.5 Анализ задачи
- 1.6 Выбор переменных и параметров
- 1.7 Определение связей и ограничений
- 1.8 Формулировка целевой функции
- 1.9 Решение и интерпретация модели
- 1.10 Вопрос-ответ:
- 1.10.0.1 Что такое математическая модель задачи?
- 1.10.0.2 Зачем нужно создавать математическую модель задачи?
- 1.10.0.3 Как построить математическую модель задачи?
- 1.10.0.4 Какие методы можно использовать для построения математической модели задачи?
- 1.10.0.5 Какие преимущества есть у построения математической модели задачи?
Статья рассказывает о том, что означает построить математическую модель задачи и как это помогает в решении сложных проблем. Описываются основные этапы построения модели и приводятся примеры из различных областей, где применяется математическое моделирование.
Математическая модель задачи — это упрощенное описание реального явления или процесса с использованием математических символов, формул и уравнений. Построение такой модели позволяет анализировать и предсказывать поведение системы, разрабатывать оптимальные решения и принимать обоснованные решения.
Для построения математической модели необходимо провести анализ задачи, выделить основные параметры и связи между ними, а также определить цель и ограничения решения. Затем выбираются подходящие математические модели и методы, которые позволят описать и решить задачу.
Одним из ключевых этапов построения математической модели является формализация. Это процесс перевода реальных данных и условий задачи в математические термины. Для этого используются переменные, функции, уравнения и неравенства, которые отражают связи и зависимости между параметрами системы.
Пример:
Представим, что мы хотим оптимизировать процесс производства товаров. Для этого необходимо построить математическую модель, которая учтет такие параметры, как стоимость сырья, объем производства, затраты на труд и т.д. Мы можем использовать различные математические модели, такие как линейное программирование, динамическое программирование или симуляцию, чтобы определить оптимальные значения параметров и принять решение, которое приведет к максимальной прибыли.
Важно отметить, что математическая модель является аппроксимацией реальной ситуации и не всегда полностью отражает все ее аспекты. Однако, правильно построенная модель может быть полезным инструментом для исследования и решения сложных задач в различных областях, таких как экономика, физика, биология и др.
Что такое математическая модель
Математическая модель может быть использована в различных областях, таких как физика, экономика, биология, информатика и т. д. Она позволяет исследовать и предсказывать поведение системы, оптимизировать ее параметры и принимать взвешенные решения на основе математических анализов и расчетов.
Примером математической модели может служить модель движения тела под действием гравитации. В этом случае, тело описывается дифференциальным уравнением, где учитываются масса тела, его начальное положение и скорость, а также сила гравитации. Решая данное уравнение, можно определить траекторию движения тела в пространстве и время его пребывания в определенных точках.
Построение математической модели требует абстрактного мышления, умения выделять главные факторы и взаимосвязи в задаче, а также знания математических методов и техник. Важно сформулировать явные и точные условия задачи, а также правильно выбрать подходящие математические инструменты.
Видео по теме:
Зачем нужна математическая модель

Зачастую задачи, стоящие перед нами, слишком сложны и многогранны, чтобы решить их методами простого наблюдения или эксперимента. Математическая модель позволяет анализировать систему в различных условиях, прогнозировать ее поведение и оптимизировать процессы. Благодаря моделированию можно провести виртуальные эксперименты и получить результаты, которые может быть сложно или невозможно получить в реальности.
Математическая модель позволяет предсказывать будущие события, оптимизировать ресурсы и принимать обоснованные решения. Она также может использоваться для поиска решений в сложных задачах оптимизации, построения прогнозов, определения границ допустимых значений и т.д. Математическая модель является мощным инструментом для анализа и решения проблем в различных областях знаний и научных исследований.
Одним из преимуществ математической модели является ее возможность быть проверенной и корректированной с помощью экспериментов и наблюдений. После построения модели и проведения эксперимента можно сравнить полученные результаты и сделать выводы о ее точности и адекватности. Это позволяет улучшать модель и делать ее более точной и надежной.
Использование математической модели позволяет существенно экономить время, ресурсы и усилия при решении сложных задач. Она помогает увидеть скрытые закономерности, определить важные факторы и взаимосвязи, а также предсказать результаты решений. Математическая модель – это мощный инструмент, который позволяет упростить и ускорить процесс анализа и принятия решений.
Построение математической модели

Процесс построения математической модели включает в себя несколько шагов:
1. Определение цели моделирования: необходимо четко определить, какая информация требуется получить с помощью математической модели. Это может быть предсказание поведения системы, оптимизация решения, описание взаимодействия компонентов и т.д.
2. Идентификация входных и выходных данных: необходимо определить, какие данные требуется использовать в модели и какие результаты необходимо получить. Входные данные могут включать параметры системы, начальные условия, ограничения и т.д., а выходные данные — результаты моделирования.
3. Выбор подходящих математических методов: на этом этапе выбираются математические методы, которые позволят описать систему в виде уравнений или алгоритмов. Это может включать дифференциальные уравнения, статистические методы, оптимизацию и т.д.
4. Построение математической модели: данный шаг включает перевод реальной ситуации или системы в математические уравнения или алгоритмы. Здесь необходимо учесть все входные данные и ограничения, а также выбранные математические методы.
5. Валидация и верификация модели: после построения модели необходимо проверить ее правильность и адекватность. Валидация модели осуществляется путем сравнения результатов моделирования с экспериментальными данными или уже известными решениями. Верификация модели предполагает проверку правильности математических уравнений и алгоритмов, используемых в модели.
Построение математической модели требует глубокого понимания реальной ситуации или системы, а также знания математических методов и инструментов. Корректно построенная модель позволяет анализировать и предсказывать поведение системы, оптимизировать решения и принимать обоснованные решения на основе математических данных.
Анализ задачи
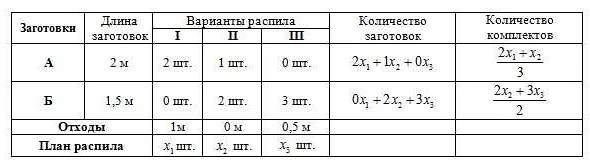
Перед тем как построить математическую модель задачи, необходимо провести анализ самой задачи. Анализ задачи позволяет понять ее суть, выделить основные компоненты и взаимосвязи между ними.
Во время анализа задачи следует обратить внимание на следующие аспекты:
- Цель задачи: определить, какое конкретное решение требуется получить. Цель может быть выражена в виде математической функции, ограничений на переменные или определенных условий, которые должны быть удовлетворены.
- Переменные: выделить все переменные задачи, т.е. величины, которые могут меняться и влиять на решение. Переменные могут быть числовыми, булевыми или категориальными.
- Ограничения: определить все ограничения, которые накладываются на переменные. Ограничения могут быть линейными или нелинейными, равенствами или неравенствами.
- Функция цели: если задача требует оптимизации, то необходимо определить функцию цели, которую нужно минимизировать или максимизировать.
- Дополнительные условия: выделить любые дополнительные условия, которые могут влиять на решение задачи. Например, наличие ограничений по времени, ресурсам или другим факторам.
Анализ задачи помогает сформировать понимание о ее структуре и основных компонентах. Это является важным шагом перед построением математической модели, так как позволяет определить, какие переменные и ограничения должны быть включены в модель. Также анализ задачи помогает определить, какие методы и алгоритмы можно применить для решения задачи.
Выбор переменных и параметров
Выбор переменных и параметров зависит от конкретной задачи и ее условий. Например, при моделировании движения тела можно выбрать переменными его координаты и скорости, а параметрами — массу и силы, действующие на тело. В другой задаче выбор переменных и параметров может быть совершенно иным.
При выборе переменных и параметров необходимо учитывать цель построения модели и требования, предъявляемые к ее точности и адекватности. Важно выбрать те переменные и параметры, которые максимально точно описывают систему и позволяют решить поставленную задачу.
Для удобства организации информации о переменных и параметрах часто используется таблица. В таблице указываются названия переменных и параметров, их обозначения, значения и единицы измерения. Такая таблица помогает лучше структурировать информацию и облегчить понимание модели.
НазваниеОбозначениеЗначениеЕдиницы измерения
| Масса тела | m | 10 | кг |
| Координата | x | 5 | м |
| Скорость | v | 2 | м/с |
В данной таблице приведены примеры переменных и параметров для моделирования движения тела. Они выбраны с учетом условий задачи и позволяют описать движение тела с необходимой точностью.
Определение связей и ограничений
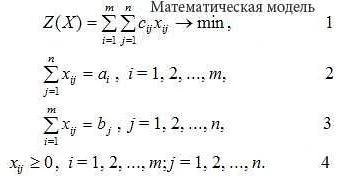
Ограничения, в свою очередь, определяют допустимые значения переменных и параметров модели. Они устанавливают границы, в пределах которых должны находиться значения переменных, чтобы модель была реалистичной и соответствовала реальным условиям задачи.
Определение связей и ограничений требует внимательного анализа и понимания самой задачи. Необходимо выявить все взаимосвязи между различными элементами задачи и ограничения, которые должны быть учтены.
Процесс определения связей и ограничений часто включает в себя использование математических выражений, уравнений и неравенств. Они позволяют формализовать связи между переменными и установить допустимые значения для них.
Важно отметить, что определение связей и ограничений является неотъемлемой частью работы по построению математической модели задачи. От правильного определения связей и ограничений зависит точность и достоверность модели, а также ее способность предсказывать и решать реальные задачи.
Формулировка целевой функции
Целевая функция может иметь различные формы в зависимости от типа модели и поставленных задач. Она может быть линейной или нелинейной, одномерной или многомерной.
Формулировка целевой функции включает в себя переменные, которые нужно определить, условия ограничений и требования к оптимальному решению.
Примеры целевых функций:
- Минимизация суммарных затрат на производство
- Максимизация прибыли
- Минимизация времени выполнения задачи
- Максимизация эффективности работы системы
Формулировка целевой функции является важным этапом построения математической модели задачи. От правильного определения цели зависит корректность и эффективность решения задачи.
Решение и интерпретация модели

После построения математической модели задачи, следует перейти к ее решению. Задача решается с использованием различных методов и алгоритмов, которые зависят от специфики задачи и доступных инструментов.
В процессе решения модели, осуществляется подстановка значений в уравнения, вычисление математических операций и получение ответа на поставленную задачу. Здесь важно соблюдать точность вычислений и знание математических методов и правил, чтобы не допустить ошибок.
Полученный ответ на задачу должен быть проинтерпретирован и переведен в понятную для заказчика или пользователя форму. Интерпретация модели включает объяснение смысла полученных результатов и их значимости для решения реальной проблемы или задачи.
Часто в процессе интерпретации модели используются графические или визуальные методы для наглядного представления данных. Это может быть построение графиков, диаграмм, таблиц или других визуальных элементов, которые помогут понять и проиллюстрировать полученные результаты.
Интерпретация модели также включает оценку точности и надежности полученных результатов. Необходимо провести анализ ошибок и погрешностей, которые могут возникнуть в процессе решения модели, и оценить их влияние на достоверность результатов. Это позволяет сделать выводы о применимости модели и ее полезности в решении конкретной задачи.
В целом, решение и интерпретация математической модели задачи – это важный шаг в процессе анализа данных и принятия решений. От качества решения и адекватности интерпретации зависит успешность применения модели для решения реальных задач и достижения поставленных целей.
Вопрос-ответ:
Что такое математическая модель задачи?
Математическая модель задачи — это абстрактное представление реальной задачи с использованием математических символов и формул. Она позволяет описать основные свойства и взаимосвязи объектов и явлений задачи, исследовать их поведение и предсказывать результаты.
Зачем нужно создавать математическую модель задачи?
Создание математической модели позволяет формализовать реальную задачу и решать ее с использованием математических методов и инструментов. Это позволяет упростить анализ задачи, предоставить возможность проводить эксперименты и исследования виртуально, а также прогнозировать результаты различных вариантов решения задачи.
Как построить математическую модель задачи?
Для построения математической модели задачи необходимо следовать определенным шагам. Сначала нужно определить, какие объекты и явления будут участвовать в модели, а затем выделить основные свойства и взаимосвязи между ними. Далее следует выбрать математические символы и формулы, которые будут использоваться для описания этих свойств и взаимосвязей. Важно учесть, что математическая модель должна быть адекватной и достаточно точно отражать реальные явления задачи.
Какие методы можно использовать для построения математической модели задачи?
Для построения математической модели задачи можно использовать различные методы, в зависимости от типа задачи и ее особенностей. Например, для задач оптимизации можно применять линейное или нелинейное программирование, для анализа систем массового обслуживания — теорию очередей, для моделирования случайных процессов — теорию вероятностей и статистику. Важно выбрать наиболее подходящий метод для конкретной задачи.
Какие преимущества есть у построения математической модели задачи?
Построение математической модели задачи имеет ряд преимуществ. Во-первых, это позволяет сделать задачу формальной и упростить ее анализ. Во-вторых, модель позволяет проводить эксперименты и исследования виртуально, без необходимости реального выполнения задачи. В-третьих, математическая модель позволяет прогнозировать результаты различных вариантов решения задачи и выбрать оптимальный. В-четвертых, модель может быть использована для обучения и тренировки, позволяя практиковаться в решении задач и улучшать свои навыки.

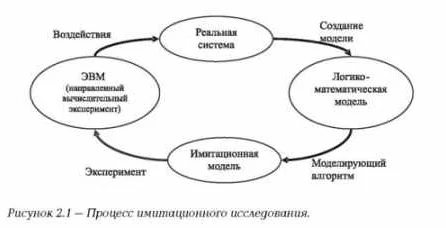


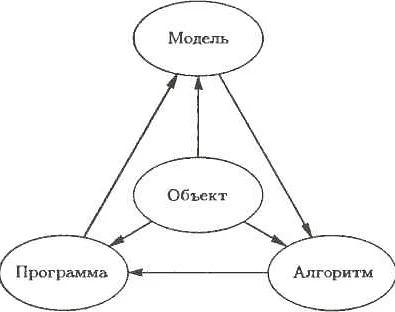
Математическая модель задачи — это способ представить реальную ситуацию в виде формальной математической структуры, которая позволяет решить данную проблему. Построение такой модели требует точного описания всех факторов, влияющих на задачу, и их взаимосвязей. Важно понимать, что математическая модель — это упрощенное отражение реальности, но она позволяет увидеть основные закономерности и взаимосвязи, что помогает найти оптимальное решение. Для построения модели нужно выделить ключевые переменные и параметры проблемы, определить их взаимосвязи и применить математические уравнения или функции для их описания. Основные шаги построения математической модели: 1. Определить цель задачи и необходимые данные. 2. Выделить ключевые переменные и параметры. 3. Описать взаимосвязи между переменными и параметрами. 4. Представить эти взаимосвязи в виде математических уравнений или функций. 5. Разработать методы для решения модели и анализа полученных результатов. Построение математической модели позволяет увидеть проблему с новой стороны, выявить важные факторы и найти оптимальное решение. Важно помнить, что модель является упрощенным отражением реальности, поэтому результаты моделирования всегда нужно проверять на практике.
Математическая модель задачи — это абстрактное представление реальной ситуации, состоящее из математических уравнений и формул. Она позволяет описать и изучить различные явления и процессы, которые происходят в реальных системах. Построение математической модели требует умения абстрагироваться от лишних деталей и выделить основные компоненты задачи. Для построения модели необходимо сначала определить цель и задачу, которую нужно решить. Затем анализируются все факторы, влияющие на систему, и выделяются основные переменные, которые нужно учесть. Далее формулируются уравнения, описывающие взаимодействие этих переменных и их изменение со временем. Важно учитывать, что математическая модель является упрощенным представлением реальности и может не учесть все факторы и условия. Поэтому модель всегда требует проверки и корректировки на основе экспериментальных данных. Построение математической модели — это сложный процесс, требующий знаний математики и умения применять их на практике. Однако, благодаря моделированию, мы можем получить новые знания о системах и прогнозировать их поведение в различных ситуациях.
Статья очень интересная и понятная. Она помогла мне разобраться, что такое математическая модель задачи и как ее построить. Я всегда думал, что математика – это сложно и непонятно, но статья объяснила все так просто и доступно. Теперь я понимаю, что математическая модель – это способ описать реальную проблему с помощью математических формул и уравнений. А самое главное – статья подробно рассказала, как построить такую модель. Теперь я уверен, что смогу применить эти знания на практике. Спасибо автору за полезную информацию!