Что такое мд в математике

МД в математике означает мощность или кардинальность множества, то есть количество элементов в нем. Узнайте, как определить МД и как она используется в различных областях математики.

Математическое доказательство – это логическое обоснование и объяснение истинности утверждений в математике. Оно играет важную роль в развитии математики и является неотъемлемой частью математической науки. Одним из наиболее распространенных методов доказательства является метод математической индукции, или МД.

МД – это метод доказательства, который позволяет доказывать утверждения для всех натуральных чисел, начиная с некоторого базового значения. Он основан на принципе математической индукции, который утверждает, что если утверждение верно для некоторого числа n, и его истинность доказана для n+1, то оно верно для всех натуральных чисел больших или равных n.

Например, для доказательства того, что сумма первых n натуральных чисел равна n*(n+1)/2, мы можем использовать метод математической индукции. Базовое значение – n=1, истинность утверждения проверяется непосредственно. Далее, предполагая, что утверждение верно для n, мы доказываем его истинность для n+1. Таким образом, мы можем убедиться, что сумма первых n натуральных чисел равна n*(n+1)/2 для всех натуральных чисел n.

Метод математической индукции широко применяется в различных областях математики, включая алгебру, комбинаторику, математическую логику и теорию чисел. Он позволяет строить формальные доказательства для множества утверждений и теорем, что делает его мощным инструментом в математике.

Математическое доказательство: что это такое, определение и примеры

Определение математического доказательства может варьироваться в зависимости от используемой логической системы или математической теории. Однако в целом доказательство включает следующие основные шаги:

1. Формулировка утверждения, которое требуется доказать.
2. Использование определений, аксиом и ранее доказанных теорем для вывода промежуточных утверждений.
3. Построение цепочки логических выводов, которые позволяют перейти от начального утверждения к целевому утверждению.
4. Проведение формальной проверки логической последовательности и корректности применяемых выводов.

Математическое доказательство должно быть строго и логически корректным, чтобы его можно было признать валидным. В математике существуют различные методы и техники доказательства, такие как доказательство от противного, математическая индукция, доказательство по методу математического анализа и т. д.

Примером математического доказательства может служить доказательство теоремы Пифагора. В этом доказательстве используется геометрическая конструкция, которая показывает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Таким образом, математическое доказательство является важной составляющей математической науки, которая позволяет устанавливать и подтверждать истинность математических утверждений.

Определение МД в математике

Математическая дедукция имеет строгую структуру и состоит из последовательности логических шагов. Она начинается с набора аксиом, которые считаются истинными без доказательства. Затем применяются правила вывода, которые позволяют строить новые утверждения, основываясь на уже известных.

Процесс МД включает в себя логические операции, такие как конъюнкция, дизъюнкция, отрицание и импликация. Он также может использовать кванторы всеобщности и существования для формулировки утверждений.

Примером МД может служить доказательство теоремы Пифагора в геометрии. Начиная с определенных аксиом, с помощью логических правил и законов, можно получить утверждение о квадрате гипотенузы прямоугольного треугольника, который равен сумме квадратов катетов.

Основные принципы МД

Принцип непротиворечивости: Математическое доказательство должно быть свободно от противоречий. Это означает, что доказательство не должно содержать логических ошибок или противоречивых утверждений.

Принцип строгости: Доказательство должно быть строго построено на базе аксиом и ранее доказанных утверждений. Каждый шаг в доказательстве должен быть логически обоснован и приводить к следующему утверждению или результату.

Принцип полноты: Доказательство должно охватывать все необходимые аргументы и утверждения для подтверждения истинности или ложности утверждения. Не должно быть пропущенных шагов, которые могут повлиять на окончательный результат.

Принцип простоты: Доказательство должно быть понятным и простым для понимания. Использование четкой и логической структуры, а также простых и понятных доказательственных методов делает доказательство более доступным для аудитории.

Принцип универсальности: Доказательство должно быть верным для всех возможных случаев и условий, в которых применяется утверждение. Доказательство не должно быть ограничено на определенный диапазон значений или условий.

Соблюдение этих основных принципов МД позволяет математикам создавать надежные и точные доказательства, которые подтверждают истинность и ложность математических утверждений.

Примеры МД в математике

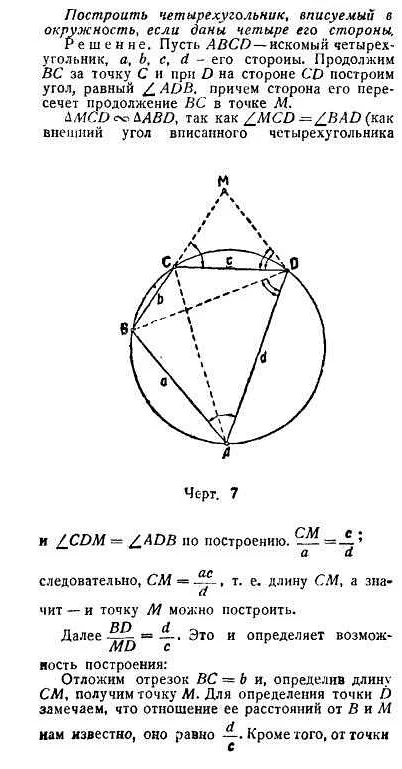
ПримерОписание

1	Доказательство теоремы о трех перпендикулярах: если две прямые пересекаются и образуют перпендикулярные углы с третьей прямой, то эти две прямые являются перпендикулярами друг к другу.
2	Доказательство теоремы Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
3	Доказательство формулы для суммы арифметической прогрессии: сумма первых n членов арифметической прогрессии равна половине произведения суммы первого и последнего членов на их количество.

Это лишь некоторые примеры МД в математике. Все они используют логические шаги и математические концепции для достижения точного и объективного результата.

МД и формулировка теоремы

Формулировка теоремы — это точное и строгое выражение математического утверждения, которое требуется доказать. Формулировка теоремы должна быть ясной, четкой и однозначной, чтобы избежать возможных двусмысленностей и непонимания.

Важной частью формулировки теоремы является ее условие, которое описывает предположения и ограничения, необходимые для применения теоремы. Также в формулировке теоремы присутствует тезис, который описывает утверждение, подлежащее доказательству.

Пример формулировки теоремы:

Теорема	В любом треугольнике сумма мер двух углов всегда меньше 180 градусов.
Условие	Треугольник ABC, где A, B и C — вершины треугольника.
Тезис	Сумма мер угла A и угла B меньше 180 градусов.

Таким образом, формулировка теоремы является основой для доказательства математических утверждений и позволяет устанавливать новые факты в математике.

Различные типы МД

Математическая демонстрация (МД) может принимать различные формы и использоваться для разных целей. Вот некоторые из типов МД, которые широко используются в математике:

Аксиоматическая МД: Это тип МД, который основан на наборе аксиом и правил вывода. Аксиомы являются базовыми утверждениями, которые принимаются без доказательства. Правила вывода позволяют строить логические цепочки, которые приводят к доказательству или опровержению математических утверждений.

Комбинаторная МД: В этом типе МД используются комбинаторные методы для доказательства математических утверждений. Комбинаторика изучает комбинаторные структуры, такие как перестановки, сочетания и разбиения, и их свойства. Комбинаторные методы могут использоваться для решения задач, связанных с перечислением и подсчетом объектов.

Алгебраическая МД: Этот тип МД использует алгебраические методы, такие как операции над числами, уравнения и системы уравнений, для доказательства математических утверждений. Алгебраическая МД может быть использована для решения уравнений и систем уравнений, а также для доказательства алгебраических свойств и тождеств.

Геометрическая МД: Этот тип МД использует геометрические методы и свойства фигур для доказательства математических утверждений. Геометрическая МД может быть использована для доказательства теорем в планиметрии (геометрии на плоскости) и стереометрии (геометрии в пространстве).

Теоретическая МД: В этом типе МД используются теоретические методы и концепции для доказательства математических утверждений. Теоретическая МД может быть применена к различным областям математики, включая теорию чисел, теорию графов, теорию множеств и математическую логику.

Вероятностная МД: Этот тип МД использует вероятностные методы и статистическую теорию для доказательства математических утверждений. Вероятностная МД может быть применена для моделирования случайных событий и различных вероятностных процессов.

Компьютерная МД: В этом типе МД используются компьютерные методы и алгоритмы для доказательства математических утверждений. Компьютерная МД может включать использование компьютерных программ и символьных вычислений для проведения сложных вычислений и проверки математических утверждений.

Важно отметить, что эти типы МД не являются исчерпывающими, и в математике также используются другие типы доказательств, а также комбинации различных методов и подходов.

МД и логические операции

Существует несколько основных логических операций, используемых в МД. Первая из них — конъюнкция (логическое «и»). Она обозначается символом ∧ и возвращает истинное значение только в случае, если оба операнда истинны. Например, выражение «2 > 1 ∧ 3 > 2» будет истинным, так как оба условия выполняются.

Вторая логическая операция — дизъюнкция (логическое «или»). Она обозначается символом ∨ и возвращает истинное значение, если хотя бы один из операндов истинен. Например, выражение «2 > 1 ∨ 3 < 2» также будет истинным, так как хотя и второе условие не выполняется, первое условие верно.

Третья логическая операция — отрицание (логическое «не»). Она обозначается символом ¬ и меняет значение операнда на противоположное. Например, если у нас есть условие «2 > 1», то его отрицание будет «¬(2 > 1)», что равно «1 > 2».

Логические операции позволяют строить сложные логические выражения и использовать их в МД. Например, мы можем составить выражение «¬(2 > 1) ∨ (3 < 2)», которое будет истинным, поскольку хотя первое условие ложно, второе условие — истинно.

Роль МД в математическом исследовании

Метод дифференциальных уравнений (МД) играет важную роль в математическом исследовании, позволяя моделировать и анализировать разнообразные процессы и явления в различных областях науки и техники.

МД является мощным инструментом для описания динамических систем, в которых изменение некоторой величины зависит от ее текущего значения и ее производной по времени. Это может быть, например, движение тела под действием силы, распространение тепла, распад радиоактивного вещества и многое другое.

Метод дифференциальных уравнений позволяет строить математические модели, которые отражают поведение системы во времени. Эти модели могут быть использованы для прогнозирования будущих состояний системы, определения устойчивости или неустойчивости ее равновесных состояний, а также для исследования различных свойств системы.

Применение МД в математическом исследовании позволяет не только получить качественное понимание поведения системы, но и проводить количественный анализ. С помощью различных методов решения дифференциальных уравнений, таких как метод Эйлера или метод Рунге-Кутты, можно получить численные решения и численно исследовать систему в различных условиях.

Метод дифференциальных уравнений также находит применение во многих конкретных областях науки и техники. Например, в физике МД позволяют описывать движение тел, в экономике — моделировать экономические процессы, в биологии — моделировать популяционную динамику, а в инженерии — анализировать и проектировать системы управления.

Таким образом, МД являются неотъемлемым инструментом математического исследования, позволяющим анализировать и описывать сложные динамические системы в различных областях науки и техники.

Значимость МД в математическом образовании

Знание МД позволяет учащимся не только понимать математические теоремы, но и уметь их доказывать. Это развивает у них уверенность в своих математических способностях и способствует формированию критического мышления.

Важно отметить, что МД является неотъемлемой частью математического рассуждения. Он позволяет учащимся объяснять и обосновывать свои решения, а также строить логическую цепочку аргументов.

Применение МД в математическом образовании помогает учащимся решать сложные задачи, а также развивать навыки абстрактного мышления и творческого подхода к решению задач.

Таким образом, МД играет важную роль в математическом образовании, поскольку способствует развитию логического мышления, аналитических навыков и критического мышления у учащихся.

Вопрос-ответ:

Что такое МД в математике?

МД в математике – это сокращение от «метод доказательства». Это способ решения математических задач, основанный на логическом выводе, аксиомах и правилах суждения.

Какие существуют примеры МД в математике?

Примеры МД в математике включают метод математической индукции, доказательство от противного, доказательство с помощью контрапозиции, доказательство по определению и другие. Все они являются различными способами логического вывода, используемыми для доказательства математических утверждений.

Можете привести пример МД в математике?

Конечно! Один из примеров МД в математике – это метод математической индукции. Например, для доказательства формулы для суммы первых n натуральных чисел: 1 + 2 + 3 + … + n = n*(n+1)/2, можно использовать метод математической индукции. Сначала доказывается базовое утверждение для n = 1, затем предполагается, что утверждение верно для некоторого n, и доказывается, что оно верно и для n+1. Таким образом, используя логический вывод, можно доказать данную формулу для всех натуральных чисел n.

Какие еще методы доказательства существуют в математике?

В математике существует множество методов доказательства, включая доказательство от противного, доказательство с помощью контрапозиции, доказательство по определению, методы доказательства эквивалентности, методы доказательства существования и единственности, методы доказательства необходимости и достаточности и многие другие. Каждый метод имеет свои особенности и применяется в зависимости от конкретной математической задачи.

Видео по теме: