Какой этап предполагает метод математической индукции

Метод математической индукции предполагает проведение доказательства для всех чисел из условного множества, начиная с базового шага и затем переходя к индуктивному шагу. В этом методе используется логическое заключение, основанное на предположении, что если утверждение верно для одного числа, то оно верно и для следующего числа. Таким образом, этапы метода математической индукции включают формулировку базового шага, подтверждение этого шага, формулировку индуктивного предположения и доказательство индуктивного шага для всех чисел из условного множества.

Метод математической индукции – это один из основных инструментов математического доказательства, используемый для доказательства утверждений о целых числах. Он является мощным и эффективным средством, позволяющим доказывать верность утверждений для всех натуральных чисел.

Этот метод состоит из нескольких этапов. Первый этап – база индукции. На этом этапе проверяется верность утверждения для начального значения, чаще всего для числа 1 или 0. Если утверждение верно для базы индукции, то переходим ко второму этапу.

Второй этап – предположение индукции. На этом этапе предполагается, что утверждение верно для некоторого фиксированного числа n. Это называется предположением индукции или индукционным предположением. Затем необходимо доказать, что из предположения индукции следует верность утверждения для числа n+1.

Третий этап – шаг индукции. На этом этапе доказывается, что из предположения индукции следует верность утверждения для числа n+1. Это выполняется с помощью математических рассуждений и логических операций. Если шаг индукции успешно выполнен, то утверждение считается доказанным для всех натуральных чисел.

Метод математической индукции является мощным инструментом для доказательства утверждений о целых числах. Он позволяет провести строгие логические рассуждения, основываясь на базовом случае и предположении индукции. Данный метод широко применяется в различных областях математики, физики и информатики, и является фундаментальным элементом математического анализа.

Что такое метод математической индукции

Метод математической индукции состоит из трех основных этапов:

1. База индукции: доказательство утверждения для начального значения. Здесь проверяется истинность утверждения для самого первого значения, например, для n=1.
2. Предположение индукции: предполагается, что утверждение верно для некоторого значения n=k.
3. Шаг индукции: доказательство утверждения для следующего значения n=k+1, основываясь на предположении индукции и рекурсивной зависимости.

Метод математической индукции широко используется в математике для доказательства различных теорем, формул и свойств. Он позволяет построить строгую логическую цепочку рассуждений и обосновать верность утверждений для всех значениях.

Видео по теме:

Этапы метода

Метод математической индукции состоит из следующих этапов:

1. Базовый шаг: На этом этапе необходимо доказать, что утверждение верно для начального значения, чаще всего это $n=1$ или $n=0$. Это является основной основой для дальнейшего применения метода.

2. Предположение: На данном этапе предполагается, что утверждение верно для некоторого значения $n=k$, т.е. $P(k)$ истинно. Это называется предположением индукции.

3. Индукционный шаг: Следующий этап — доказательство, что утверждение также верно для значения $n=k+1$. Для этого необходимо использовать предположение индукции, т.е. предположить, что $P(k)$ верно, и из этого сделать вывод, что тогда верно и $P(k+1)$. Это обычно делается путем применения математических операций или логических рассуждений.

4. Заключение: На последнем этапе нужно сделать вывод, что утверждение верно для всех значений $n$, начиная с базового значения. Это может быть сделано путем объединения базового шага и индукционного шага.

Таким образом, метод математической индукции состоит из простых, но последовательных этапов, позволяющих доказать верность утверждений для всех значений $n$.

База математической индукции

На этом этапе нужно показать, что утверждение верно для начального значения, обычно для наименьшего натурального числа. В математической индукции начальное значение обозначается как n = 1 (или другое заданное начальное значение).

Чтобы доказать базу математической индукции, необходимо выполнить следующие шаги:

1. Указать, что предполагается доказать для начального значения n.
2. Продолжить с предположением, что утверждение верно для n.
3. Доказывать утверждение для n+1, используя предположение индукции.
4. Показать, что утверждение верно для n+1.

База математической индукции является основой для индуктивного доказательства, и если база верна, то можно перейти к следующему этапу — индуктивному переходу.

Важно отметить, что база математической индукции должна быть верна для всех натуральных чисел, а не только для одного конкретного значения. Если база не выполняется, то индуктивное доказательство не будет корректным.

Вопрос-ответ:

Какие этапы включает метод математической индукции?

Метод математической индукции включает следующие этапы: база индукции, предположение индукции и шаг индукции.

Что такое база индукции в методе математической индукции?

Базой индукции в методе математической индукции называется утверждение, которое проверяется непосредственно и служит основой для доказательства утверждений для всех натуральных чисел.

В чем особенность метода математической индукции?

Особенностью метода математической индукции является то, что он позволяет доказывать утверждения для всех натуральных чисел, используя базу индукции, предположение индукции и шаг индукции.

Какой пример можно привести для наглядного объяснения метода математической индукции?

Примером для наглядного объяснения метода математической индукции может служить доказательство формулы для суммы арифметической прогрессии.

Переход по индукции

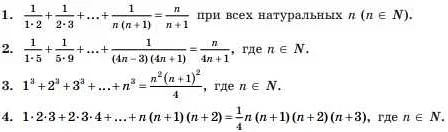
После того, как мы доказали базу индукции и предположение индукции, необходимо совершить переход от n к n+1.

Для этого нужно доказать, что если утверждение верно для некоторого числа n, то оно верно и для числа n+1.

Переход по индукции может быть выполнен различными способами, в зависимости от самой задачи и используемых инструментов.

Однако, в большинстве случаев, переход по индукции осуществляется посредством логических рассуждений и применения

уже доказанного утверждения для числа n к числу n+1.

Чтобы успешно совершить переход по индукции, необходимо внимательно анализировать условия задачи и применять

соответствующие математические методы и свойства.

Во время перехода по индукции можно использовать различные приемы, такие как алгебраические преобразования,

замена переменных, применение индукционной гипотезы и т.д.

Переход по индукции является важной частью метода математической индукции и позволяет установить истинность

утверждения для всех натуральных чисел.

Шаг индукцииДоказываемое утверждениеДоказательство

База индукции	Утверждение верно для n=1	Доказываемое утверждение для n=1
Переход по индукции	Утверждение верно для n	Доказываемое утверждение для n+1

Доказательство справедливости

Доказательство справедливости включает в себя несколько этапов. На первом этапе необходимо проверить, что утверждение верно для начального значения, обычно это число 1. Если утверждение верно при n = 1, то можно считать, что оно верно и для всех следующих натуральных чисел.

На втором этапе необходимо доказать, что если утверждение верно для некоторого числа k, то оно верно и для числа k + 1. Для этого предполагают, что утверждение верно при n = k, и на основе этого предположения доказывают его справедливость при n = k + 1. Этот шаг называется переходом.

Третий этап заключается в выводе того, что утверждение верно для всех натуральных чисел. Этот вывод основывается на первых двух этапах. Изначально утверждение верно при n = 1. Затем, используя переход, мы доказываем, что если оно верно для некоторого k, то оно верно и для k + 1. Таким образом, утверждение верно для 1, затем для 2, затем для 3 и так далее.

Доказательство справедливости метода математической индукции является формальным и строгим процессом. Оно обязательно должно включать все три этапа, и каждый из них должен быть доказан с использованием логических рассуждений.

Поэтому при использовании метода математической индукции необходимо провести доказательство справедливости, чтобы убедиться в его корректности и достоверности. Это позволяет использовать метод индукции как надежный инструмент для решения математических задач и доказательства различных утверждений.

Особенности метода

1. Базовый шаг: проверяется истинность утверждения для некоторого начального значения (чаще всего для значения 1 или 0).
2. Шаг индукции: предполагается, что утверждение выполняется для некоторого значения n. Далее, используя это предположение, доказывается, что утверждение также выполняется для значения n+1.

Основные особенности метода математической индукции:

• Метод индукции позволяет доказывать утверждения для бесконечного множества значений, основываясь на доказательстве только для нескольких начальных значений.
• Метод индукции позволяет упростить доказательство сложных математических утверждений, разбивая их на более простые шаги.
• Метод индукции требует строгого и логически верного построения доказательства, чтобы быть корректным.
• Метод индукции может быть применен не только в математике, но и в других областях науки, где требуется доказательство утверждений.

Использование метода математической индукции требует понимания его особенностей и правильного применения. Этот метод является мощным инструментом для доказательства математических утверждений и находит широкое применение в различных областях науки.

Применимость метода математической индукции

Применение метода математической индукции обычно включает в себя следующие этапы:

1. База индукции: В этом этапе проверяется истинность утверждения для начального значения (например, для n = 1). Это является основой для последующего доказательства.
2. Предположение индукции: В этом этапе предполагается, что утверждение верно для некоторого значения n = k. Это предположение делается для доказательства истинности утверждения для следующего значения n = k + 1.
3. Доказательство шага индукции: В этом этапе показывается, что если утверждение верно для n = k, то оно также верно для n = k + 1. Это позволяет сделать вывод о верности утверждения для всех натуральных чисел, начиная с базы индукции.

Применимость метода математической индукции определяется структурой утверждения и его зависимостью от натуральных чисел. Если утверждение можно разделить на серию независимых шагов, каждый из которых может быть доказан с использованием предыдущего шага, то метод индукции может быть применен.

Однако, следует отметить, что метод математической индукции не является универсальным и не может быть применен во всех математических задачах. Иногда, для доказательства утверждений требуются другие методы и подходы, такие как доказательство от противного, математическая инфекция и т. д.

Ограничения метода математической индукции

1. Ограничение на тип утверждений: Метод математической индукции может быть применен только для доказательства утверждений, которые можно выразить в форме «для всех натуральных чисел». Это ограничение означает, что метод не может быть использован для доказательства утверждений, которые зависят от других типов чисел, таких как дроби, отрицательные числа или действительные числа.
2. Ограничение на базовый случай: Метод требует явного указания базового случая, который является начальной точкой для индуктивного рассуждения. Если базовый случай неправильно выбран или отсутствует, то метод может дать неверные результаты. Поэтому выбор правильного базового случая является важным шагом в применении метода.
3. Ограничение на шаг индукции: Метод требует явного указания шага индукции, который связывает утверждение для числа n с утверждением для числа n+1. Если шаг индукции неправильно сформулирован или неверно доказан, то метод может дать неверные результаты. Поэтому правильная формулировка и доказательство шага индукции также являются важными шагами в применении метода.
4. Ограничение на множество целей: Метод математической индукции может быть применен только для доказательства утверждений, которые верны для всех натуральных чисел. Если требуется доказать утверждение, которое верно только для определенного подмножества натуральных чисел, то метод может быть неэффективным или неприменимым.

Несмотря на эти ограничения, метод математической индукции остается мощным инструментом для доказательства многих утверждений в математике. С правильным выбором базового случая, формулировкой и доказательством шага индукции, а также ограничением на тип утверждений и множество целей, метод может быть успешно применен для доказательства множества математических утверждений.

Плюсы использования метода математической индукции

1. Универсальность: Метод математической индукции может быть применен для доказательства утверждений в самых различных областях математики, а также в других науках, где используется формальное рассуждение.

2. Простота: Основная идея метода индукции заключается в разбиении доказательства на несколько простых шагов. Это делает процесс доказательства более понятным и доступным для понимания.

3. Экономия времени и усилий: Используя метод индукции, можно доказать утверждение для бесконечного числа значений переменной, выполнив всего лишь несколько шагов. Это значительно сокращает количество вычислений и упрощает доказательство.

4. Общность вывода: Если утверждение доказано для всех натуральных чисел, то оно будет верно для любого конкретного значения переменной. Это позволяет получать общие выводы и обобщать результаты на другие задачи и проблемы.

В целом, использование метода математической индукции позволяет систематизировать и упорядочить процесс доказательства математических утверждений, а также придать им строгий и надежный характер.

Минусы использования метода математической индукции

• Сложность в применении: метод математической индукции требует от математика определенных навыков и умений. Не всегда легко разделить доказательство на базовый шаг и шаг индукции, а также правильно выбрать предположение индукции.
• Ограничение области применения: метод математической индукции может быть использован только для доказательства утверждений, имеющих структуру, где шаг от одного значения к следующему осуществим.
• Не всегда удается найти базовый шаг: в некоторых случаях сложно найти первое значение, для которого утверждение верно.
• Ограничение на класс задач: метод математической индукции применяется только для решения математических задач. В других областях знаний, где требуется доказательство, этот метод может быть неприменим.
• Ограничение на тип утверждений: метод математической индукции не может быть использован для доказательства неравенств и некоторых других сложных утверждений.