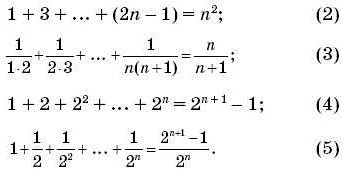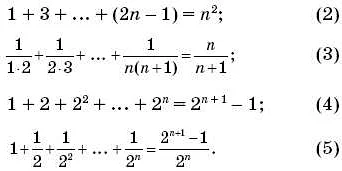Метод математической индукции: суть и правила применения

Метод математической индукции – это способ доказательства утверждений в математике, который основывается на рассмотрении базового случая и предположения о верности утверждения для n и вывода верности утверждения для n+1, что позволяет доказать его для всех натуральных чисел. В статье описывается принцип метода и его применение на примерах.

Метод математической индукции — это один из основных методов доказательства утверждений в математике. Он используется для доказательства утверждений, которые верны для всех натуральных чисел, то есть для бесконечного множества чисел. Такой подход позволяет избежать необходимости доказывать каждый случай отдельно и сделать вывод о верности утверждения в целом.

Основной принцип метода математической индукции заключается в доказательстве утверждения для базового случая (обычно это натуральное число 1) и доказательстве, что из верности утверждения для любого числа n следует его верность для числа n+1. Из этих двух шагов следует, что утверждение верно для всех натуральных чисел.

Метод математической индукции широко используется в различных областях математики, включая алгебру, геометрию, теорию чисел, теорию графов и другие. Он также имеет множество применений в информатике и программировании, в том числе для доказательства корректности алгоритмов и программных функций.

В этой статье мы рассмотрим более подробно принцип работы метода математической индукции и приведем несколько примеров его применения в различных областях математики и информатики.

Метод математической индукции

Метод математической индукции – это математический метод, используемый для доказательства утверждений вида «Для всех натуральных чисел n…».

Этот метод состоит из двух шагов:

1. База индукции. Доказать утверждение для начального значения, например, для n=1.
2. Шаг индукции. Предположить, что утверждение верно для произвольного значения n=k, и показать, что из этого следует, что утверждение верно и для значения n=k+1.

Таким образом, если мы доказали базу индукции и убедились, что для любого k соответствующее утверждение верно, мы можем заключить, что оно верно для всех натуральных чисел.

Пример использования метода математической индукции – доказательство формулы суммы арифметической прогрессии:

1. База индукции. Для n=1 утверждение верно, так как сумма первого члена равна самому первому члену.
2. Шаг индукции. Пусть утверждение верно для n=k, то есть сумма первых k членов равна (k/2)(2a+(k-1)d). Тогда сумма первых (k+1) членов равна сумме первых k членов плюс (k+1)-й член, то есть (k/2)(2a+(k-1)d)+(a+kd). После простых преобразований мы получим (k+1)/2(2a+k*d), что и является утверждением для n=k+1.

Таким образом, по индукции мы доказали формулу суммы арифметической прогрессии для любого натурального числа n.

Видео по теме:

Описание метода

Метод математической индукции является принципиальным инструментом математического доказательства утверждений, выраженных в терминах целых чисел.

По сути, метод заключается в проверке верности утверждения для начального значения n=1, а затем в доказательстве, что если это утверждение справедливо для всех целых значений n

Таким образом, математическая индукция может использоваться для доказательства различных утверждений, включая формулы, равенства и неравенства, а также свойства чисел и функций.

Применение метода математической индукции является важным элементом математического анализа и доказательств, используемых в различных областях науки и техники.

Одним из примеров применения метода математической индукции является доказательство суммы арифметической прогрессии, что широко используется при решении задач во многих приложениях математики и физики.

Пример применения

Используя метод математической индукции, мы можем доказать многие утверждения в математике. В качестве примера рассмотрим формулу для суммы арифметической прогрессии:

Утверждение: Для любых натуральных чисел n и m, где m ≥ n, справедлива формула:

1 + 2 + 3 + … + n = n(n+1)/2

База индукции: При n = 1, выражение слева равно 1, а выражение справа равно 1(1+1)/2 = 1. Таким образом, база индукции доказана.

Предположение: Предположим, что при фиксированном k, где k ≥ 1, формула также справедлива:

1 + 2 + 3 + … + k = k(k+1)/2

Шаг индукции: Докажем, что утверждение также верно при n = k+1:

1 + 2 + 3 + … + k + (k+1) = (k+1)((k+1)+1)/2

Раскроем скобки:

k(k+1)/2 + (k+1) = (k+1)(k+2)/2

Приведем к общему знаменателю:

k(k+1)/2 + 2(k+1)/2 = (k+1)(k+2)/2

(k^2 + 3k + 2)/2 = (k+1)(k+2)/2

Оба выражения равны, что и требовалось доказать.

Таким образом, мы доказали формулу для суммы арифметической прогрессии с помощью метода математической индукции.

Вопрос-ответ:

Как работает метод математической индукции?

Метод математической индукции состоит из двух шагов: базовый шаг и шаг индукции. Базовый шаг доказывает истинность утверждения для начального значения. Затем, шаг индукции доказывает, что если утверждение верно для некоторого числа n, то оно верно и для числа n+1. Сложив эти два шага вместе, мы можем доказать истинность утверждения для всех натуральных чисел.

Какие примеры можно решить, используя метод математической индукции?

Метод математической индукции может использоваться для решения различных задач. Некоторые примеры из области алгебры включают доказательство формул факториала, поиска сумм арифметических последовательностей и доказательство неравенств. В геометрии, метод математической индукции может использоваться для доказательства формулы для суммы углов в многоугольнике или для доказательства теоремы Пифагора.

Как я могу использовать метод математической индукции для доказательства неравенства?

Допустим, у вас есть неравенство типа S(n)

Может ли метод математической индукции использоваться для доказательства истинности сложных высказываний?

Метод математической индукции может использоваться для доказательства истинности сложных высказываний, если они могут быть сформулированы как утверждения о натуральных числах. Однако, доказательство сложных высказываний может потребовать более сложных доказательств, чем только метод математической индукции.

В каких случаях можно применять метод математической индукции?

Метод математической индукции можно применять в случаях, когда нужно доказать утверждение, которое зависит от натурального числа n, и которое имеет рекурсивную структуру. Он также эффективен для доказательства формул, которые зависят от n, таких как формула для факториала или формула для суммы арифметической последовательности.

Какой базовый шаг нужен для проведения метода индукции?

Базовый шаг для метода математической индукции — это доказательство утверждения для начального значения, которое обычно равно 1. Для большинства рекурсивных формул, которые мы хотим доказать, базовый случай обычно является простым утверждением, которое можно проверить непосредственно. Если мы не можем доказать утверждение для базового значения, то мы не можем провести шаг индукции.

Как часто используется метод математической индукции в математике?

Метод математической индукции часто используется в математике, особенно в области доказательства теорем. Он может быть использован для доказательства формул, неравенств, и более сложных утверждений. Он также используется в компьютерных науках и в других областях, где требуется доказательство утверждения зависящих от натуральных чисел.

Принцип работы

Метод математической индукции — это математический метод доказательства утверждений для всех натуральных чисел. Он основан на двух шагах: базовом и индукционном.

Базовый шаг заключается в доказательстве утверждения для первого натурального числа, то есть показать, что утверждение верно для числа 1.

Индукционный шаг заключается в доказательстве, что если утверждение верно для некоторого произвольного натурального числа n, то оно верно и для числа n+1. Для этого нужно воспользоваться принципом математической индукции: сначала проверить базовый шаг, а затем доказать, что выполнение индукционного шага следует из выполнения утверждения для числа n.

Принцип математической индукции — это не только метод доказательства теорем, но и метод решения задач и нахождения общих формул. Он широко применяется в алгебре, геометрии, теории чисел, математической логике и других разделах математики.

Примеры задач

Принцип математической индукции широко используется для решения задач в различных областях математики, физики и информатики. Ниже приведены несколько примеров задач, которые можно решить с помощью метода математической индукции:

Пример 1

Доказать, что сумма первых n нечетных чисел равна n^2.

Решение:

1. Базис. При n = 1, сумма первых n нечетных чисел равна 1^2 = 1. Утверждение верно для n = 1.
2. Индукционный переход. Предположим, что утверждение верно для некоторого n = k. Нужно доказать, что утверждение верно и для n = k + 1.
   • Сумма первых k нечетных чисел равна k^2.
   • Добавляем (k + 1)-e нечетное число, которое равно 2k + 1. Тогда сумма первых (k + 1) нечетных чисел равна k^2 + 2k + 1 = (k + 1)^2.

   Утверждение верно и для n = k + 1.

Доказали, что утверждение верно для всех n из N.

Пример 2

Доказать, что для любого натурального числа n: 1*2 + 2*3 + … + n*(n+1) = n*(n+1)*(n+2)/3.

Решение:

1. Базис. При n = 1, 1*2 = 1*(1+1)*(1+2)/3 = 2/3. Утверждение верно при n = 1.
2. Индукционный переход. Пусть нам уже известно, что утверждение верно при n = k. Нужно доказать, что утверждение верно также при n = k + 1.
   • 1*2 + 2*3 + … + k*(k+1) = k*(k+1)*(k+2)/3.
   • Добавляем (k+1)*(k+2) к левой и правой частям:1*2 + 2*3 + … + k*(k+1) + (k+1)*(k+2) = k*(k+1)*(k+2)/3 + (k+1)*(k+2).
   • Приводим к общему знаменателю:3*1*2 + 3*2*3 + … + 3*k*(k+1) + 3*(k+1)*(k+2) = (k+1)*(k+2)*(k+3)/3.
   • Приводим подобные:3*(1*2 + 2*3 + … + k*(k+1)) + 3*(k+1)*(k+2) = (k+1)*(k+2)*(k+3)/3.
   • Пользуемся индукционным предположением:3*k*(k+1)*(k+2)/3 + 3*(k+1)*(k+2) = (k+1)*(k+2)*(k+3)/3.
   • Упрощаем:(k+1)*(k+2)*(k+3)/3 = (k+1)*(k+2)*(k+3)/3.

   Утверждение верно также при n = k + 1.

Доказали, что утверждение верно для всех n из N.

Пример 3

Доказать, что для любого натурального числа n, существует бинарный код длины 2^n, который не содержит двух соседних единиц.

Решение:

1. Базис. При n = 1, существует бинарный код 01, который не содержит двух соседних единиц. Утверждение верно при n = 1.
2. Индукционный переход. Предположим, что утверждение верно для некоторого n = k. Нужно доказать, что утверждение верно и для n = k + 1.
   • Для n = k, существует бинарный код длины 2^k, который не содержит двух соседних единиц.
   • Добавляем слева к каждому коду из предыдущего пункта 0, а справа — 1 (т.е. получаем все возможные комбинации для k + 1 разряда). Например, если предыдущий код 001, то мы получаем 0001 и 0011.
   • Полученные коды не содержат двух соседних единиц. В самом деле, если бы код содержал две единицы рядом, они обязательно были бы в конце. Но мы добавили 1 только справа, так что в этом случае были бы две единицы рядом и в предыдущем коде, что противоречит предположению.

   Утверждение верно и для n = k + 1.

Доказали, что утверждение верно для всех n из N.

Условия применения

Метод математической индукции применяется для доказательства утверждений, которые имеют общую формулировку для всех натуральных чисел. При этом, для правильного применения метода необходимо соблюдать следующие условия:

• База индукции: необходимо доказать утверждение для наименьшего значения переменной. Обычно это значение равно 1, но может быть и другим. База индукции должна быть верна.
• Индукционный переход: необходимо доказать, что если утверждение верно для произвольного, но фиксированного, значения переменной, то оно верно и для следующего значения. Для этого используется предположение индукции. Индукционный переход должен быть верен.
• Однократность применения: метод математической индукции необходимо применять только один раз на каждое утверждение. Это означает, что если утверждение можно доказать с помощью метода индукции, то оно не может быть доказано этим же методом еще раз.

Важно понимать, что метод математической индукции не является универсальным и не может быть использован для доказательства любых утверждений. Он применяется только в тех случаях, когда утверждение имеет общую формулировку для всех натуральных чисел и соблюдаются условия применения метода.

Особенности рассуждений

Метод математической индукции позволяет прийти к выводу о верности некоторого утверждения для всех натуральных чисел. В процессе рассуждений необходимо учитывать несколько особенностей.

• Начальное условие: чтобы применить метод индукции, необходимо убедиться в верности утверждения для первого натурального числа, то есть для n=1.
• Индукционный переход: следующий шаг заключается в доказательстве того, что если утверждение верно для n=k, то оно верно и для n=k+1. Этот шаг называют индукционным переходом.
• Предположение индукции: при доказательстве верности утверждения для n=k+1 необходимо использовать предположение индукции, сделанное на шаге n=k.
• Ограничивающий фактор: при применении метода индукции необходимо учитывать возможные ограничения, которые могут возникнуть в процессе рассуждений.

Важно помнить, что использование метода индукции требует строгой логической последовательности и точности аргументации. Незначительная ошибка на одном из шагов может привести к неверному выводу о верности утверждения для всех натуральных чисел.

Примеры применения на практике

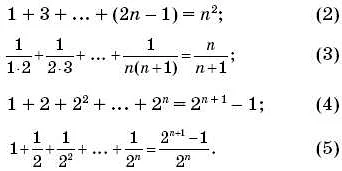
Пример 1: Метод математической индукции используется в теории вероятности для доказательства формулы Бернулли. При этом, индуктивный шаг заключается в доказательстве формулы для n + 1 испытания, при условии, что она справедлива для n испытаний.

Пример 2: Метод математической индукции может использоваться для доказательства формул для вычисления сумм арифметических, геометрических прогрессий и их общих формул. Индуктивный шаг в этом случае состоит в доказательстве формулы для n + 1 элемента, при условии что она верна для n элементов.

Пример 3: Метод математической индукции применяют в алгебре для доказательства различных утверждений. Например, доказательство, что для любых натуральных чисел a и b, a^2 — b^2 делится на (a + b).

Пример 4: Метод математической индукции используется для доказательства неравенства между арифметическим и геометрическим средними для положительных чисел. Индуктивный шаг заключается в использовании неравенства о треугольнике и разложении выражения на произведение.

Пример 5: Метод математической индукции применяется для доказательства различных теорем в теории чисел, таких как теорема о делении с остатком, теорема Вильсона и многие другие.

Пример 6: Метод математической индукции может использоваться при доказательстве сложных алгоритмов в информатике, таких как доказательство корректности алгоритмов сортировки и поиска в деревьях.

Пример 7: Метод математической индукции используется в различных научных исследованиях, как основной метод доказательства теорем и утверждений.

Таким образом, метод математической индукции находит широкое применение не только в математике, но и в других областях знаний, где требуется доказательство утверждений с помощью формализованных методов.

Плюсы метода

Простота и логичность: Математическая индукция исходит из базовых утверждений, которые принимаются как аксиомы. С помощью последовательных шагов, к этим утверждениям добавляются новые факты, в результате чего получается верное утверждение.

Универсальность: Метод индукции может применяться в широком диапазоне задач, таких как доказательство формул, алгоритмов и различных утверждений. Кроме того, он используется в математической и теоретической физике, информатике, экономике и других научных областях.

Доказательство правильности алгоритмов: Метод индукции может быть использован для доказательства правильности алгоритмов, что делает его очень полезным в программировании и информатике. При этом, математический алгоритм не обязательно должен быть сложным: индукция может быть использована для доказательства простых утверждений.

Экономия времени: Применение метода математической индукции позволяет доказывать верность утверждений без необходимости проверки всех возможных случаев. Таким образом, данный метод экономит время и усилия, которые обычно тратятся на проверку каждого случая отдельно.

Наглядность: Доказательство с помощью метода индукции находит свое применение как в науке, так и в повседневной жизни. Например, если мы хотим показать, что каждый шестизначный номер телефона может быть прочитан и запомнен, то индуктивный аргумент основывается на том, что если мы можем запомнить первые пять цифр телефонного номера, то мы можем запомнить и весь номер.

Минусы метода

Хотя метод математической индукции является мощным инструментом для доказательства утверждений, он также имеет ряд недостатков, которые стоит учитывать.

• Не всегда возможно найти базовый случай — существуют задачи, для которых сложно определить начальное условие, необходимое для применения метода индукции.
• Доказательства с помощью метода индукции могут быть длинными и сложными, особенно в случае не очень простых рекурсивных формул.
• Существует опасность использования метода индукции для доказательства неверного утверждения. Несмотря на то, что метод индукции является строгим, построение неправильной базы или перехода может привести к ошибочному выводу.
• Этот метод не подходит для доказательств утверждений, которые не являются последовательностями или рекурсивными.

Поэтому следует помнить, что метод математической индукции — это всего лишь инструмент, который может применяться в определенных случаях и не является универсальным решением всех математических задач.