Матрица в математике что это такое и зачем
Содержимое
- 1 Матрица в математике что это такое и зачем
Матрица в математике – это таблица чисел, упорядоченных по строкам и столбцам. Матрицы используются для решения различных задач, таких как линейные уравнения, системы уравнений, преобразования координат и многое другое. Узнайте, как матрицы помогают в решении сложных математических задач и как они связаны с различными областями науки и техники.
Матрица – это одна из основных концепций линейной алгебры, используемая в математике и других науках. Она представляет собой прямоугольную таблицу чисел или символов, расположенных в виде строк и столбцов. Матрицы широко применяются в различных областях, таких как физика, экономика, компьютерная графика и многие другие.
Зачем нужна матрица?
Матрицы позволяют компактно и удобно представлять и обрабатывать большие объемы данных. Они используются для решения систем линейных уравнений, аппроксимации и интерполяции функций, в задачах оптимизации, разложении сигналов и многих других задачах. Более того, матрицы обладают рядом важных свойств и операций, которые делают их незаменимым инструментом при решении многих математических задач.
В данной статье мы рассмотрим основные понятия и операции с матрицами, а также рассмотрим некоторые примеры их применения. При изучении матриц необходимо обратить внимание на их структуру, следующие операции: сложение, умножение, транспонирование, их свойства и возможные применения в реальной жизни.
Матрица в математике
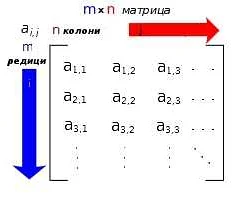
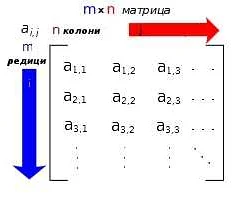
Матрицы широко используются в различных областях, включая физику, экономику, компьютерную графику и машинное обучение. Они позволяют представлять и обрабатывать данные с помощью математических операций.
Матрицы могут иметь разные размеры и свойства. Количество строк и столбцов в матрице называется ее размерностью. Например, матрица размером 2×3 имеет 2 строки и 3 столбца.
Операции над матрицами включают сложение, вычитание, умножение и транспонирование. Сложение и вычитание матриц выполняются покомпонентно, то есть складываются или вычитаются соответствующие элементы. Умножение матрицы на число и на другую матрицу также выполняется покомпонентно или с использованием специальных формул.
Матрицы позволяют решать системы линейных уравнений, находить обратные матрицы, находить собственные значения и собственные векторы, а также выполнять другие операции, которые широко применяются в науке и технике.
Таким образом, матрица является важным и мощным инструментом в математике и ее применение особенно актуально в современном информационном обществе.
Определение матрицы

Матрицы широко используются в математике, физике, экономике и других науках для представления и обработки данных. Они позволяют компактно и структурированно хранить информацию, а также выполнять различные операции, такие как сложение, вычитание, умножение и транспонирование.
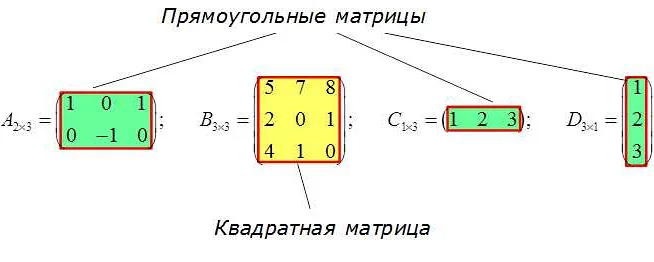
Количество строк и столбцов в матрице называется ее размерностью. Матрицы могут быть квадратными (когда количество строк равно количеству столбцов) или прямоугольными.
Элементы матрицы обозначаются символами, обычно заглавными латинскими буквами. Каждый элемент матрицы находится на пересечении строки и столбца и имеет свою позицию, которая определяется номером строки и номером столбца.
| a11 | a12 | a13 |
| a21 | a22 | a23 |
| a31 | a32 | a33 |
В данном примере представлена матрица размерности 3×3, состоящая из 9 элементов.
Размерность матрицы
Например, если у нас есть матрица размером 3×4, это означает, что в ней 3 строки и 4 столбца. Количество элементов в такой матрице будет равно произведению количества строк и столбцов, то есть 3 * 4 = 12.
Размерность матрицы имеет большое значение при выполнении операций с матрицами. Важно учитывать, что при сложении или умножении матрицы на число или на другую матрицу, их размерности должны быть согласованы. Например, для сложения двух матриц их размерности должны совпадать, то есть обе матрицы должны иметь одинаковое количество строк и столбцов.
Размерность матрицы также определяет ее тип. Матрицы могут быть квадратными, если у них одинаковое количество строк и столбцов, или прямоугольными, если количество строк и столбцов различно.
Операции с матрицами
В математике существуют различные операции, которые можно выполнять с матрицами:
- Сложение матриц: чтобы сложить две матрицы, их размерности должны быть одинаковыми. Сложение происходит поэлементно, то есть каждый элемент первой матрицы складывается с соответствующим элементом второй матрицы.
- Вычитание матриц: аналогично сложению, размерности матриц должны быть одинаковыми. Вычитание также происходит поэлементно — каждый элемент первой матрицы вычитается из соответствующего элемента второй матрицы.
- Умножение матриц: для умножения двух матриц их размерности должны удовлетворять определенному условию. Умножение также происходит поэлементно, но результатом является новая матрица, размерность которой зависит от размерности исходных матриц.
- Транспонирование матрицы: при транспонировании матрицы ее строки становятся столбцами, а столбцы — строками. Таким образом, получается новая матрица с измененными размерностями.
- Умножение матрицы на число: при умножении матрицы на число, каждый элемент матрицы умножается на это число.
- Обратная матрица: обратная матрица существует только для квадратных матриц определенного типа. Обратная матрица удовлетворяет определенному условию, при умножении исходной матрицы на обратную получается единичная матрица.
Операции с матрицами являются важной темой в линейной алгебре и имеют множество практических применений. Понимание и умение выполнять эти операции позволяет решать различные задачи и анализировать данные в различных областях науки и техники.
Умножение матриц
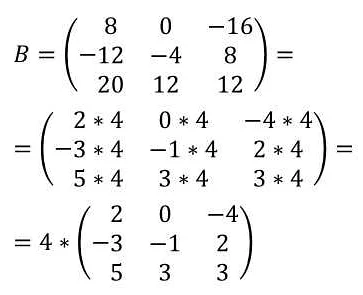
Для умножения матриц A и B необходимо, чтобы количество столбцов матрицы A было равно количеству строк матрицы B. Если это условие выполняется, то элемент новой матрицы C[i][j] получается путем умножения соответствующих элементов i-й строки матрицы A на j-й столбец матрицы B и их суммирования.
Таким образом, если A — матрица размерности m x n, а B — матрица размерности n x k, то результатом их умножения будет матрица C размерности m x k, где C[i][j] равно сумме произведений элементов i-й строки матрицы A на j-й столбец матрицы B.
Умножение матриц является важной операцией во многих областях, таких как линейная алгебра, теория вероятностей, физика, экономика и компьютерная графика. Оно используется для решения систем линейных уравнений, вычисления определителей и обратных матриц, а также для преобразования координат в трехмерном пространстве.
Системы линейных уравнений
Для решения системы линейных уравнений с помощью матриц необходимо сначала записать систему в матричной форме. Для этого неизвестные переменные записываются в виде вектора, а коэффициенты перед ними — в матрицу. Затем система уравнений записывается в виде произведения этой матрицы на вектор неизвестных переменных, равного вектору свободных членов. Таким образом, система уравнений сводится к уравнению вида Ax = b, где A — матрица коэффициентов, x — вектор неизвестных, b — вектор свободных членов.
После записи системы в матричной форме можно приступить к решению. Для этого применяются различные методы, основанные на преобразовании матрицы A. Один из таких методов — метод Гаусса. Суть метода Гаусса заключается в приведении матрицы A к ступенчатому виду путем выполнения элементарных преобразований над строками. Затем с помощью обратных ходов метода Гаусса находятся значения неизвестных переменных.
Системы линейных уравнений и матрицы широко применяются в различных областях, включая физику, экономику, компьютерную графику и машинное обучение. Поэтому понимание матриц и систем линейных уравнений является важным инструментом для любого студента или специалиста в этих областях.
Пример системы линейных уравнений:
| 2x + 3y = 8 |
| 4x + 2y = 6 |
Применение матриц в графическом дизайне

Одним из основных применений матриц в графическом дизайне является трансформация объектов. С помощью матриц можно изменять размеры, поворачивать и перемещать объекты на экране. Например, при создании анимации или разработке компьютерных игр матрицы используются для анимации персонажей, движения объектов или изменения их формы.
Кроме того, матрицы позволяют преобразовывать координаты объектов в трехмерном пространстве и проецировать их на двумерную плоскость экрана. Это позволяет создавать реалистичные изображения с эффектом глубины и перспективы.
Другое важное применение матриц в графическом дизайне — текстурирование объектов. С помощью матриц можно накладывать текстуры на поверхности объектов, создавая эффекты материалов, таких как дерево, металл или стекло. Это позволяет создавать более реалистичные и привлекательные визуальные эффекты.
Также матрицы используются для обработки изображений, в том числе для наложения эффектов и фильтров. Например, с помощью матриц можно изменять яркость, контрастность, насыщенность и оттенок изображения, а также применять различные фильтры, такие как размытие, резкость или эффекты виньетки.
В целом, матрицы являются мощным инструментом в графическом дизайне, позволяющим создавать уникальные и привлекательные визуальные эффекты. Они обеспечивают большую гибкость и контроль над визуальными элементами и помогают дизайнерам воплотить свои идеи и концепции в реальность.
Применение матриц в физике

Одним из основных применений матриц в физике является описание линейных преобразований в пространстве. Линейные преобразования играют важную роль в многих физических теориях и моделях. Матрицы позволяют удобно описывать их свойства и эффекты.
Например, матрицы используются для описания поворотов и сдвигов в трехмерном пространстве. Они позволяют определить координаты точки после применения поворота или сдвига, что является важным при решении задач в различных областях физики.
Матрицы также применяются для описания волновых процессов, таких как распространение звука или света. Они позволяют представить волновую функцию и проводить операции с ней, такие как суперпозиция или дифракция.
Кроме того, матрицы используются при решении систем уравнений, которые возникают при описании физических процессов. Они позволяют эффективно решать системы уравнений и получать численные решения для различных физических величин.
Таким образом, применение матриц в физике позволяет удобно описывать и решать разнообразные задачи, связанные с физическими явлениями и процессами. Они являются важным инструментом для физиков и позволяют проводить более точные и эффективные исследования в различных областях физики.
Применение матриц в программировании
Матрицы широко применяются в программировании для решения различных задач. Они позволяют компактно хранить и оперировать множеством данных, представленных в виде таблицы. В программировании матрицы используются для работы с изображениями, графами, математическими моделями и многими другими типами данных.
Одним из основных применений матриц в программировании является работа с графиками и изображениями. Матрица пикселей изображения представляет собой двумерный массив, в котором каждый элемент содержит информацию о цвете пикселя. С помощью матриц можно выполнять множество операций над изображениями, таких как изменение размеров, фильтрация, преобразование и т.д.
Матрицы также используются для работы с графами. Графы могут быть представлены в виде матрицы смежности или матрицы инцидентности, где каждый элемент матрицы указывает на существование или отсутствие связи между вершинами графа. Это позволяет эффективно выполнять операции поиска путей, обхода графа и другие алгоритмы.
Матрицы также широко используются для решения математических задач. Например, матрицы применяются для решения систем линейных уравнений, нахождения собственных значений и векторов, аппроксимации функций и других математических операций. Также матрицы используются в различных областях программирования, таких как машинное обучение, компьютерная графика, статистика и др.
Выводящая матрица в программировании представляется в виде таблицы с ячейками, содержащими значения элементов матрицы. Это позволяет удобно отображать и визуализировать данные для анализа и обработки. Для работы с матрицами в программировании существуют специальные библиотеки и инструменты, которые предоставляют различные функции и операции для работы с матрицами.
Таким образом, матрицы играют важную роль в программировании, облегчая работу с данными различных типов и позволяя эффективно решать разнообразные задачи.
Вопрос-ответ:
Что такое матрица в математике?
Матрица — это таблица чисел, упорядоченных по строкам и столбцам. Она состоит из элементов, которые могут быть числами или другими матрицами. Матрицы используются для представления и решения различных математических задач.
Каковы основные свойства матриц?
Основные свойства матриц включают сложение, вычитание и умножение. Сложение матриц выполняется путем сложения соответствующих элементов матриц. Вычитание матриц производится аналогично. Умножение матриц осуществляется путем умножения элементов матрицы на элементы другой матрицы и сложения полученных произведений.
Зачем нужны матрицы в математике?
Матрицы используются в математике для решения систем линейных уравнений, нахождения собственных значений и собственных векторов, решения задач оптимизации, моделирования и многих других областей. Они предоставляют удобный и формализованный способ работы с большими объемами данных и комплексными математическими операциями.
Какие операции можно выполнять с матрицами?
С матрицами можно выполнять множество операций, включая сложение, вычитание, умножение, транспонирование, нахождение определителя, обратной матрицы и другие. Эти операции позволяют решать широкий спектр математических задач и применять матрицы в различных областях науки и техники.
Каким образом матрицы используются в компьютерных науках?
Матрицы широко применяются в компьютерных науках для решения задач компьютерной графики, машинного обучения, обработки изображений, распознавания образов и других областей. Они позволяют эффективно представлять и обрабатывать данные, а также решать сложные задачи, связанные с обработкой информации.
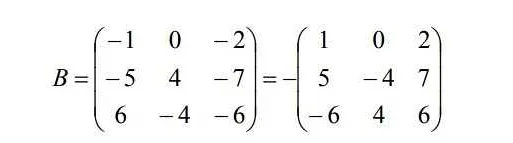
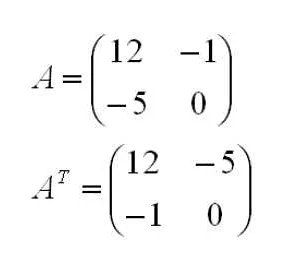

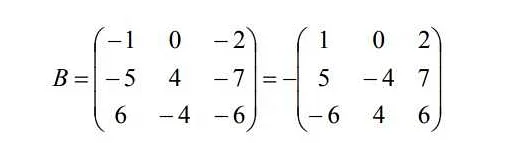
Статья очень понятно и просто объяснила суть матриц в математике. Раньше я не очень хорошо понимала, зачем они нужны и как их использовать. Но благодаря этой статье все стало ясно. Теперь я понимаю, что матрицы — это удобный инструмент для работы с различными видами данных. Они помогают решать системы линейных уравнений, анализировать и прогнозировать различные процессы. Благодаря матрицам можно упростить сложные вычисления и получить более точные результаты. Теперь я буду использовать матрицы в своих задачах и исследованиях. Спасибо за такую полезную статью!