Что означает в математике нод
Содержимое
- 1 Что означает в математике нод
НОД (наибольший общий делитель) — это математическая функция, которая находит наибольшее число, на которое одновременно делятся два или более числа. В статье рассмотрены примеры и методы вычисления НОДа, а также его важность и применение в различных областях математики и алгоритмике.
НОД (наибольший общий делитель) в математике — это одно из важнейших понятий, широко применяемое в алгебре и арифметике. Оно позволяет определить наибольший общий делитель двух или более чисел, то есть наибольшее натуральное число, на которое без остатка делятся все заданные числа.
НОД является фундаментальным понятием в теории чисел и находит свое применение во многих областях математики, включая разложение чисел на простые множители, решение уравнений, построение и анализ дробей и т.д. Он является основой для многих алгоритмов и методов решения задач, а также играет важную роль в теоретических и прикладных исследованиях.
Для нахождения НОД существуют различные методы: метод деления с остатком, алгоритм Евклида, факторизация чисел и другие. Рассмотрим примеры применения НОД для более наглядного представления. Например, для чисел 12 и 18 НОД равен 6, так как это наибольшее число, на которое делятся оба числа без остатка. Аналогично, для чисел 15 и 25 НОД равен 5. НОД можно определить не только для двух чисел, но и для любого их количества.
Определение понятия НОД

НОД является важным понятием в математике, так как позволяет решать множество задач, связанных с делимостью чисел. Например, нахождение НОД может быть полезно при упрощении дробей, нахождении наименьшего общего кратного и решении линейных диофантовых уравнений.
Пример:
Для чисел 12 и 18 НОД равен 6, так как 6 одновременно делится на оба числа без остатка, а больше число, которое бы делилось на оба числа без остатка, не существует.
Значение НОД в математике

Значение НОД в математике заключается в его применении во многих областях. Например, в арифметике НОД позволяет выполнять операции упрощения дробей. В теории чисел НОД используется для нахождения простых чисел и проверки их взаимной простоты.
НОД также находит применение в криптографии, где используется для шифрования и расшифрования данных. Он также может быть использован для решения различных задач, связанных с нахождением остатка от деления и нахождением наименьшего общего кратного двух чисел.
НОД является основным понятием в алгебре и математике в целом, и его понимание и применение имеет важное значение для решения множества задач и проблем.
Примеры использования НОД
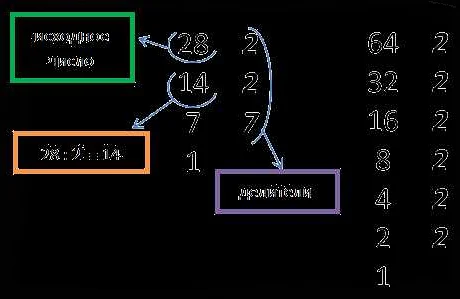
НОД (наибольший общий делитель) применяется в различных математических задачах и алгоритмах. Рассмотрим несколько примеров его использования:
1. Разложение дроби на простейшие: для упрощения дроби до простейшего вида необходимо найти НОД числителя и знаменателя. Например, для дроби 12/18 НОД чисел 12 и 18 равен 6, поэтому дробь можно упростить до 2/3.
2. Поиск наименьшего общего кратного (НОК): чтобы найти НОК двух или более чисел, можно использовать формулу НОК(a, b) = (a * b) / НОД(a, b). Например, НОК чисел 8 и 12 равен (8 * 12) / 4 = 24.
3. Решение системы линейных уравнений: для нахождения общего решения системы линейных уравнений можно использовать метод Гаусса, в котором необходимо находить НОД коэффициентов уравнений и использовать его для приведения системы к упрощенному виду.
4. Шифрование данных: НОД используется в некоторых алгоритмах шифрования, например, в алгоритме RSA. Для генерации ключей и шифрования сообщений необходимо находить НОД больших случайных чисел.
5. Определение периодичности чисел: если два числа имеют общий делитель больше единицы, то они являются периодическими десятичными дробями. Например, числа 1/3 и 2/6 имеют НОД 3, поэтому они являются периодическими дробями.
6. Поиск длины окружности: для нахождения длины окружности по ее радиусу используется формула 2 * π * r, где r — радиус. При этом, радиус и длина окружности являются пропорциональными, их НОД равен радиусу окружности.
Таким образом, НОД играет важную роль в решении различных задач в математике и других областях, где требуется нахождение общего делителя или упрощение числовых выражений.
Пример вычисления НОД
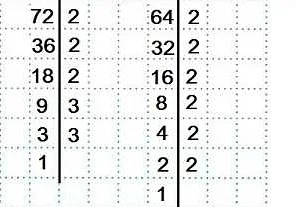
Допустим, нам нужно найти НОД двух чисел: 24 и 36. Для начала, мы можем разложить оба числа на простые множители:
- Число 24 разлагается на простые множители как 2 * 2 * 2 * 3.
- Число 36 разлагается на простые множители как 2 * 2 * 3 * 3.
Теперь, чтобы найти НОД, мы должны выбрать все общие простые множители и перемножить их вместе. В данном случае, общими простыми множителями являются 2 и 3. Перемножим их вместе:
НОД(24, 36) = 2 * 3 = 6.
Таким образом, НОД чисел 24 и 36 равен 6.
Пример применения НОД в криптографии
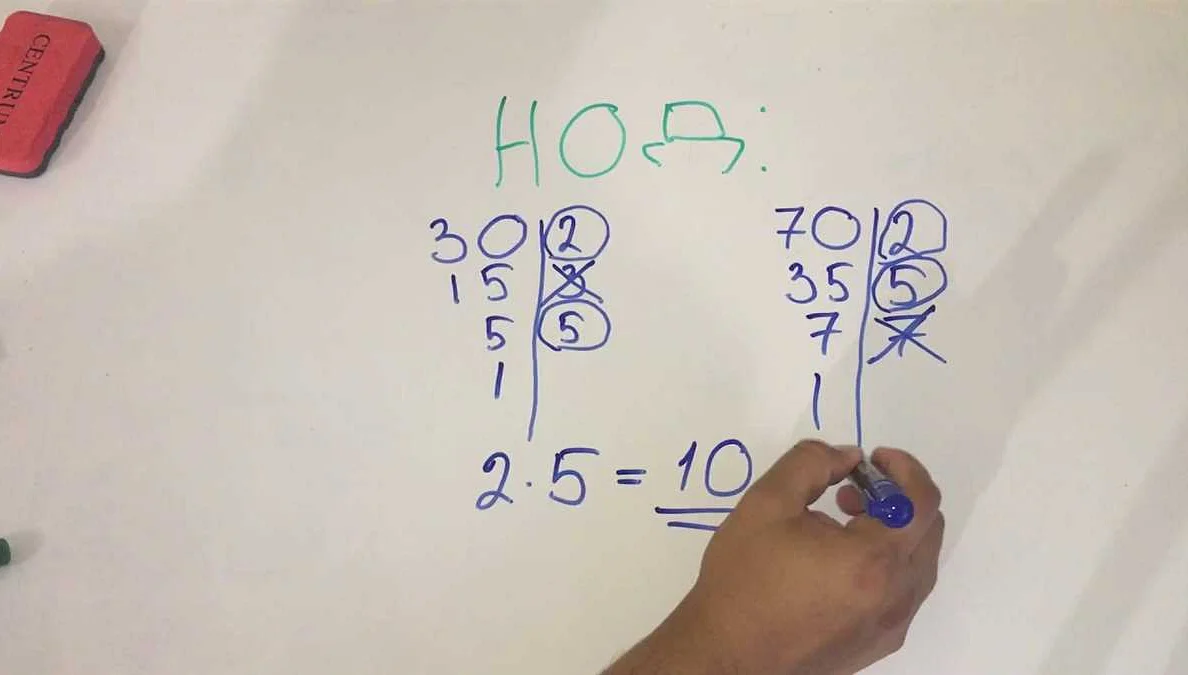
Алгоритм RSA основан на математической проблеме факторизации больших чисел. Он использует два простых числа, p и q, для генерации открытого и закрытого ключей. Открытый ключ состоит из чисел n и e, а закрытый ключ состоит из чисел n и d.
Процесс генерации ключей начинается с выбора двух различных простых чисел, p и q. Затем вычисляется их произведение, n = p * q, которое используется в качестве модуля для шифрования и дешифрования сообщений.
Далее необходимо найти значение функции Эйлера от числа n. Для этого вычисляются значения функций Эйлера для p и q, которые равны (p-1) и (q-1) соответственно. Затем находится НОД этих двух чисел, что и является значением функции Эйлера от числа n.
Зная значение функции Эйлера, выбирается открытая экспонента e, которая должна быть взаимно проста с функцией Эйлера. Это означает, что НОД(e, ф(n)) = 1, где ф(n) — значение функции Эйлера. Обычно в качестве значения e выбирают простое число, например, 65537.
Теперь необходимо найти секретную экспоненту d, которая является мультипликативно обратной к открытой экспоненте по модулю функции Эйлера. Это означает, что (e * d) mod ф(n) = 1. Для нахождения d можно использовать расширенный алгоритм Евклида или алгоритм Гаусса.
Итак, НОД применяется в алгоритме RSA для нахождения функции Эйлера и для проверки взаимной простоты открытой экспоненты и функции Эйлера. Это важные шаги для генерации безопасных ключей и обеспечения безопасности коммуникации при использовании алгоритма RSA в криптографии.
Методы вычисления НОД

Существует несколько методов для вычисления наибольшего общего делителя (НОД) двух чисел.
1. Метод деления: этот метод основан на том, что НОД двух чисел не изменится, если одно число разделить на другое с остатком, и продолжить делить делимое на полученный остаток до тех пор, пока остаток не станет равным нулю. Тогда делитель, на который разделили последний раз с остатком, будет НОД исходных чисел.
2. Метод поиска простых множителей: этот метод используется для вычисления НОД больших чисел и основан на разложении чисел на простые множители. Для каждого числа находятся его простые множители, а затем сравниваются их множества. НОД будет равен произведению всех общих простых множителей с наименьшей степенью.
3. Метод Евклида: это один из самых известных методов вычисления НОД двух чисел. Он основан на том, что НОД двух чисел равен НОДу их остатков от деления нацело. То есть, для двух чисел a и b, НОД(a, b) = НОД(b, a mod b), где «mod» означает операцию взятия остатка от деления.
Эти методы являются основными и широко используются для вычисления НОД в математике.
Метод Евклида для вычисления НОД
Для начала, необходимо записать два числа, для которых нужно найти НОД. Затем, с помощью деления с остатком, находим остаток от деления первого числа на второе. Если остаток равен нулю, то второе число и есть НОД. Если остаток не равен нулю, то второе число заменяем на остаток, а первое число становится равным второму числу. Затем повторяем процесс, пока не получим остаток равный нулю.
Пример:
Для чисел 24 и 18:
24 ÷ 18 = 1 (остаток 6)
18 ÷ 6 = 3 (остаток 0)
НОД(24, 18) = 6
В данном примере НОД чисел 24 и 18 равен 6.
Вопрос-ответ:
Что такое НОД?
НОД (наибольший общий делитель) двух или более чисел — это наибольшее число, на которое делятся все эти числа без остатка.
Как найти НОД двух чисел?
Для нахождения НОД двух чисел можно использовать алгоритм Евклида. Сначала делим большее число на меньшее и записываем остаток. Затем делим на него полученный остаток и так далее до тех пор, пока не получим ноль. Последнее ненулевое число будет НОД.
Зачем нужен НОД?
НОД используется во многих математических задачах, например, для упрощения дробей, нахождения общего знаменателя, решения линейных диофантовых уравнений и других задач.
Может ли НОД быть равен единице?
Да, НОД двух чисел может быть равен единице. В этом случае говорят, что числа являются взаимно простыми.
Как найти НОД нескольких чисел?
Для нахождения НОД нескольких чисел можно последовательно находить НОД пар чисел. Например, для чисел 12, 18 и 24 можно сначала найти НОД чисел 12 и 18, затем НОД полученного результата и числа 24.
Что такое НОД?
НОД (наибольший общий делитель) — это наибольшее целое число, которое одновременно является делителем для двух или более чисел.
Как можно найти НОД двух чисел?
Существует несколько способов нахождения НОД. Один из способов — метод Эвклида. Для нахождения НОД двух чисел нужно последовательно делить одно число на другое с остатком, затем делить полученное остаток на предыдущий остаток и так далее, пока не получим нулевой остаток. На последней итерации полученное число будет НОДом исходных чисел.
Расширенный алгоритм Евклида для вычисления НОД
Расширенный алгоритм Евклида основывается на следующем принципе: если a и b – два числа, а r – их остаток от деления, то НОД(a, b) = НОД(b, r). Используя этот принцип, мы можем последовательно находить остатки от деления и переходить к следующим парам чисел, пока не получим остаток, равный нулю. В этот момент процесс останавливается, и НОД(a, b) равен последнему ненулевому остатку.
Однако расширенный алгоритм Евклида делает шаг дальше и находит коэффициенты Безу, которые позволяют представить НОД(a, b) в виде линейной комбинации a и b.
Алгоритм можно представить в виде следующей последовательности шагов:
- Инициализировать переменные a0 = a, b0 = b, x0 = 1, y0 = 0, x1 = 0, y1 = 1.
- Вычислить q и r, где q – целая часть от деления ai-1 на bi-1, а r – остаток от деления ai-1 на bi-1.
- Установить ai = bi-1, bi = r, xi = xi-2 — qxi-1, yi = yi-2 — qyi-1.
- Повторять шаг 2 и 3, пока r не станет равным нулю.
- Коэффициенты Безу будут равными xi-2 и yi-2.
Таким образом, расширенный алгоритм Евклида позволяет эффективно находить НОД двух чисел и их коэффициенты Безу. Этот метод широко применяется в теории чисел, криптографии и других областях математики.





НОД, или наибольший общий делитель, — это математический термин, который встречается не только в учебниках, но и в повседневной жизни. Он используется для определения наименьшего числа, на которое делятся два или более числа без остатка. Это позволяет нам найти общие множители и решить различные задачи, связанные с числами. НОД имеет множество практических применений. Например, он помогает упростить дроби, факторизировать числа и решить уравнения. Кроме того, НОД используется при поиске наименьшего общего кратного (НОК) – числа, которое делится на все заданные числа без остатка. Примеры НОД могут быть разными. Например, для чисел 18 и 24 НОД равен 6, так как оба числа делятся без остатка на 6. Еще один пример – числа 15 и 25 имеют НОД, равный 5, так как оба числа делятся без остатка на 5. НОД – это неотъемлемая часть математики и является полезным инструментом для решения различных задач. Использование НОД позволяет нам лучше понимать мир чисел и их взаимосвязи.
Статья очень понятно и доступно объясняет, что такое НОД в математике. Я всегда слышал об этом понятии, но никогда не понимал его сути. Теперь все прояснилось! НОД — это наибольший общий делитель двух или более чисел. Примеры, которые приведены в статье, отлично помогли усвоить материал. Теперь я знаю, что НОД(12, 18) равен 6, так как это наибольшее число, которое одновременно делится и на 12, и на 18. Статья очень полезна и я рекомендую ее всем, кто хочет лучше понять математику и работать с числами.