Что такое планиметрия в математике

Планиметрия в математике — это раздел геометрии, изучающий фигуры и объекты на плоскости. В этой статье вы узнаете, что такое планиметрия, какие основные понятия в ней используются и как она связана с другими разделами математики.

Планиметрия – это раздел геометрии, который изучает геометрические фигуры и свойства плоских фигур. В планиметрии исследуются геометрические объекты, которые представляют собой плоские фигуры, не имеющие объема. Этот раздел математики важен для понимания и анализа различных геометрических задач в двумерном пространстве.

Основные понятия планиметрии включают в себя такие понятия, как точка, прямая, отрезок, угол, треугольник, четырехугольник, окружность и многое другое. Каждое из этих понятий имеет свои специфические свойства и характеристики, которые изучаются в рамках планиметрии.

Планиметрия находит широкое применение в различных областях, включая архитектуру, инженерное дело, геодезию, дизайн и другие. Знание планиметрии позволяет решать различные геометрические задачи, связанные с проектированием и измерениями плоских фигур. Оно также полезно для развития логического мышления, абстрактного мышления и способности к анализу и решению проблем.

Что такое планиметрия в математике

Основная задача планиметрии состоит в изучении свойств и взаимоотношений различных геометрических фигур, таких как треугольники, прямоугольники, круги и многоугольники. Планиметрия позволяет нам анализировать и решать разнообразные геометрические задачи, связанные с плоскими фигурами.

Планиметрия находит широкое применение в различных областях науки и техники, таких как архитектура, строительство, геодезия, картография и многих других. Она помогает строить и анализировать планы зданий, трассы дорог, местности и многое другое. Благодаря планиметрии мы можем более точно представлять и анализировать пространственные объекты и их свойства.

ПонятиеОписание

Длина	Выражает измерение отрезка, прямой или кривой линии в плоскости.
Площадь	Отражает размер плоской фигуры и измеряется в квадратных единицах.
Периметр	Сумма всех сторон замкнутой фигуры.
Углы	Геометрическая фигура, образованная двумя лучами, имеющими общее начало.

В заключение, планиметрия является важной и полезной областью математики, которая позволяет нам понять и описать свойства плоских фигур и применить их в различных областях жизни.

Видео по теме:

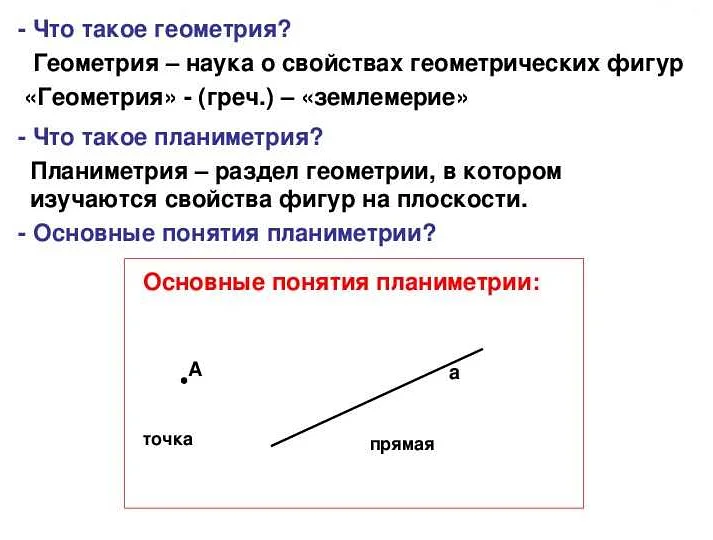
Основные понятия планиметрии

В планиметрии существуют основные понятия, которые помогают описать и анализировать геометрические объекты:

1. Точка — это элементарный объект без размеров. В планиметрии точка обозначается заглавной буквой.
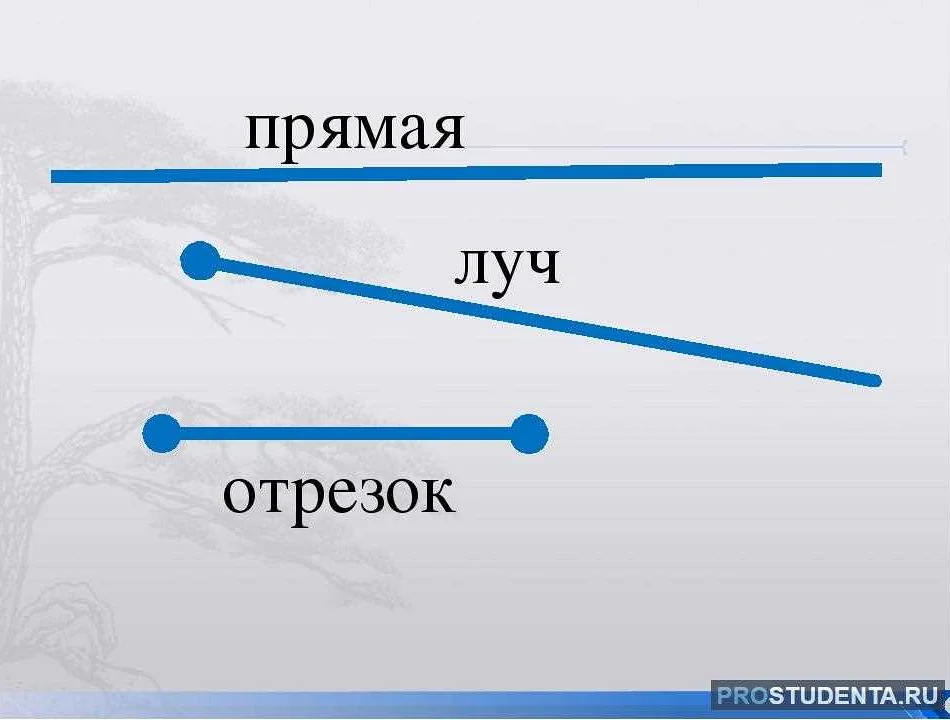
2. Прямая — это бесконечное множество точек, которые лежат на одной прямой линии. Прямую в планиметрии обозначают двумя точками, через которые она проходит.
3. Отрезок — это часть прямой, ограниченная двумя точками. Отрезок обозначается двумя точками, между которыми он расположен, и через них проводится линия.
4. Угол — это область плоскости, образованная двумя лучами, имеющими общее начало. Угол измеряется в градусах и обозначается греческой буквой альфа.
5. Многоугольник — это фигура, ограниченная отрезками, соединяющими вершины. В планиметрии многоугольник обозначается заглавной буквой, а его вершины обозначаются прописными буквами.

Основные понятия планиметрии помогают анализировать и решать задачи, связанные с геометрическими фигурами и объектами на плоскости.

Геометрические фигуры в планиметрии

Одной из основных геометрических фигур в планиметрии является треугольник. Треугольник — это фигура, состоящая из трех отрезков, называемых сторонами, и трех вершин. В зависимости от своих сторон и углов, треугольники могут быть различными: равносторонними, разносторонними, равнобедренными и прямоугольными.

Еще одной важной геометрической фигурой является круг. Круг — это множество точек, равноудаленных от одной точки, называемой центром. Круг обладает множеством свойств, таких как радиус, диаметр, длина окружности и площадь.

Прямоугольник — это четырехугольник, у которого все углы прямые. Прямоугольник имеет две параллельные стороны и четыре прямых угла. Он также имеет свойства, такие как периметр и площадь.

Ромб — это четырехугольник, у которого все стороны равны. У ромба также все углы прямые. Ромб имеет свойства, такие как диагонали, периметр и площадь.

Это лишь небольшой перечень геометрических фигур, изучаемых в планиметрии. Важно понимать, что каждая фигура имеет свои уникальные свойства и характеристики, которые широко используются в различных областях науки, техники и повседневной жизни.

Вопрос-ответ:

Что такое планиметрия и какие вопросы она изучает?

Планиметрия — это раздел геометрии, который изучает геометрические фигуры и преобразования на плоскости. В основе планиметрии лежат такие понятия, как точка, прямая, угол, треугольник, четырехугольник, круг и много других. Основные вопросы, которые решает планиметрия: измерение углов и длин, построение геометрических фигур, нахождение площадей и объемов.

Какие методы используются в планиметрии для решения задач?

В планиметрии для решения задач используются различные методы и приемы, такие как метод подобия, метод равенства площадей, метод сравнения длин, метод симметрии и многие другие. Каждый метод имеет свои особенности и применяется в зависимости от конкретной задачи.

Какие основные применения планиметрии в реальной жизни?

Планиметрия находит свое применение в различных областях, таких как архитектура, строительство, геодезия, картография и другие. Например, с помощью планиметрии можно рассчитать площадь участка земли, построить план здания или дороги, определить геометрические параметры объектов и многое другое.

Какие понятия планиметрии полезно знать для повседневной жизни?

Для повседневной жизни полезно знать такие понятия планиметрии, как площадь и периметр фигур, углы и их свойства, прямые и параллельные линии, методы измерения длин и углов. Эти знания помогут в решении различных задач, связанных с измерением и построением объектов на плоскости.

Как планиметрия связана с другими областями математики?

Планиметрия тесно связана с другими областями математики, такими как алгебра, аналитическая геометрия и теория вероятностей. Например, для решения задач в планиметрии может потребоваться использование алгебраических методов или аналитической геометрии. Также планиметрия может быть основой для изучения других разделов математики, таких как трехмерная геометрия или топология.

Теоремы планиметрии

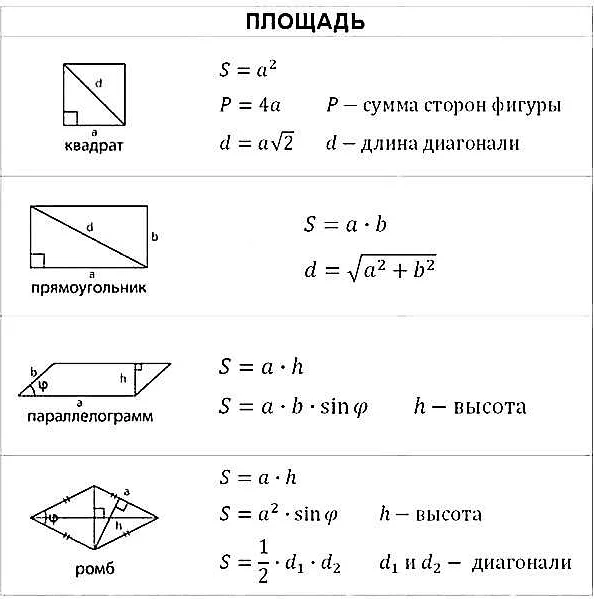
В планиметрии существует несколько основных теорем, которые описывают свойства различных фигур и помогают находить их параметры. Некоторые из наиболее известных теорем планиметрии:

Теорема Пифагора – гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Теорема Птолемея – устанавливает связь между сторонами и диагоналями четырехугольника, лежащего вокруг окружности.

Теорема Эйлера – утверждает, что сумма числа вершин, ребер и граней многогранника равна 2 плюс характеристика Эйлера данного многогранника.

Это лишь некоторые из множества теорем планиметрии, которые используются для решения различных задач. Знание этих теорем и умение применять их позволяет решать задачи геометрии на плоскости.

Планиметрические задачи

Планиметрические задачи могут быть разного типа. Например, задачи на вычисление площади фигур, нахождение длины отрезков, построение геометрических фигур и решение угловых задач. В решении планиметрических задач часто используются различные геометрические конструкции, такие как построение перпендикуляра, параллельных прямых, биссектрисы угла и другие.

Планиметрические задачи находят применение в различных областях, включая строительство, геодезию, картографию, архитектуру, дизайн и другие. Например, зная площадь участка земли, можно рассчитать количество необходимого материала для его ограждения. Знание планиметрии также полезно при построении домов, мостов, дорог и других инженерных сооружений.

Планиметрия в реальной жизни

Планиметрия, как раздел математики, широко применяется в реальной жизни, особенно в архитектуре и строительстве. Она позволяет решать разнообразные задачи, связанные с измерением и построением плоских фигур.

Планиметрия применяется при проектировании зданий и сооружений. С ее помощью можно определить площадь участка, на котором планируется строительство, а также расположение и размеры здания. Это помогает инженерам и архитекторам разрабатывать оптимальные планы и учитывать все необходимые параметры.

Еще одной сферой применения планиметрии является картография. С ее помощью составляются карты и планы городов, регионов и стран. Здесь планиметрия позволяет определить масштаб карты, измерить расстояния между объектами, а также построить планы маршрутов и путеводители.

Планиметрия также применяется в геодезии и навигации. Она помогает измерять углы и расстояния на местности, строить графики и диаграммы, а также определять координаты и высоты точек. Это важно для определения маршрутов, разработки геодезических сетей и строительства дорог и мостов.

Кроме того, планиметрия находит применение в различных научных исследованиях, где необходимо изучать и анализировать плоские фигуры и их свойства. Она также помогает в решении задач по оптимизации и моделированию.

Таким образом, планиметрия играет важную роль в реальной жизни, облегчая решение практических задач и улучшая качество проектов и исследований.

Применение планиметрии в архитектуре

Планиметрия в математике находит свое применение в различных областях, включая архитектуру. Архитектура, как и математика, требует точности и глубокого понимания пространственных отношений.

Одним из основных применений планиметрии в архитектуре является создание планов зданий и сооружений. План — это графическое представление объекта с верхнего ракурса, которое позволяет увидеть расположение помещений, стен, дверей, окон и других элементов здания. Для создания точного и функционального плана необходимо использовать методы планиметрии.

Планиметрия также помогает архитекторам решать задачи пространственного планирования. Она позволяет определить оптимальное расположение объектов на участке, зонировать пространство и создавать эргономичные и комфортные помещения. Планиметрические методы позволяют архитекторам анализировать и моделировать пространственные структуры, такие как фасады и планировочные сетки.

Кроме того, планиметрия используется при разработке и проектировании ландшафтных архитектурных объектов. Планиметрические методы позволяют определить оптимальное расположение дорожек, зон отдыха, растений и других элементов ландшафтного дизайна. Они также позволяют архитекторам учесть пропорции и гармонию при создании композиции и формы объектов.

Таким образом, планиметрия играет важную роль в архитектуре, помогая архитекторам создавать функциональные и эстетически привлекательные пространства. Она является неотъемлемой частью процесса проектирования и позволяет архитекторам достичь точности и сбалансированности в своих работах.

Применение планиметрии в геодезии

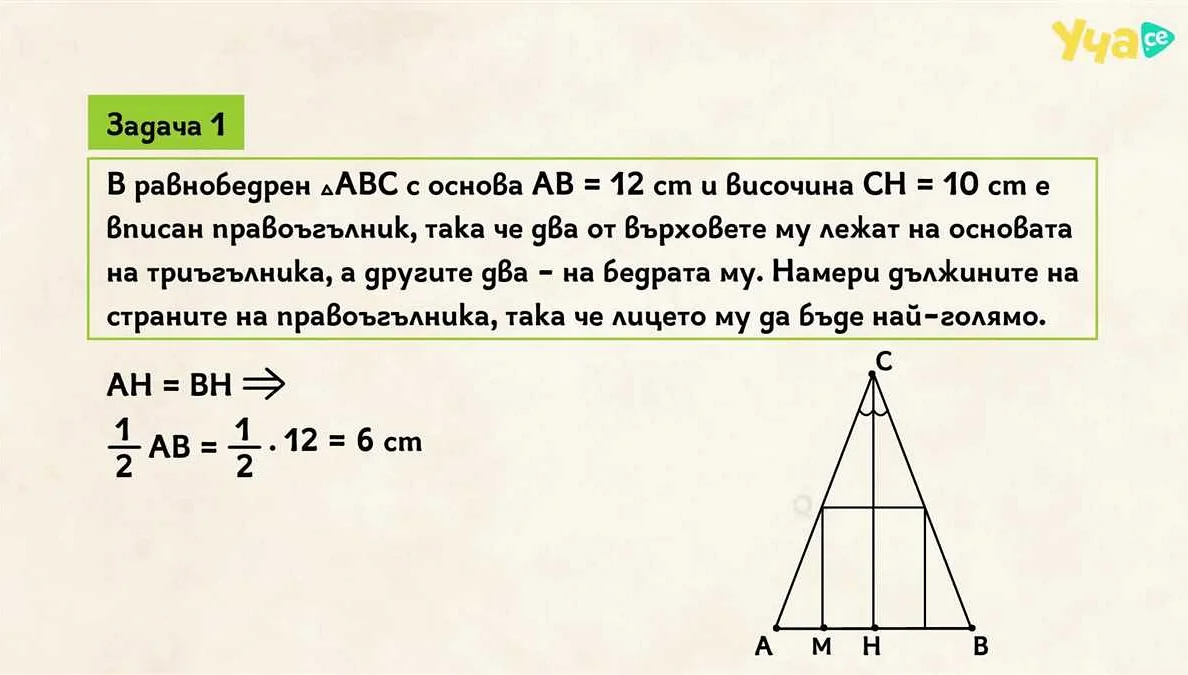
Одной из основных задач геодезии является определение площадей различных участков земли, таких как поля, лесные массивы, города и другие. Для решения этой задачи геодезисты применяют методы планиметрии. С помощью измерения сторон и углов участка земли, а также применения формул планиметрии, можно рассчитать его площадь с высокой точностью.

Планиметрия также применяется при проектировании и строительстве дорог, мостов, зданий и других инженерных сооружений. С ее помощью геодезисты могут определить точные координаты точек на поверхности земли, что необходимо для правильного расположения и построения сооружений.

В геодезии планиметрия также используется для построения карт и планов местности. С помощью планиметрических методов можно измерить и отобразить на карте различные детали ландшафта, такие как реки, озера, горы, леса и другие объекты.

Таким образом, применение планиметрии в геодезии позволяет решать различные задачи, связанные с измерением и построением плоских фигур на поверхности Земли. Она является неотъемлемой частью геодезических исследований и способствует точному определению координат и площадей различных участков земли.