Что такое полный граф в математике

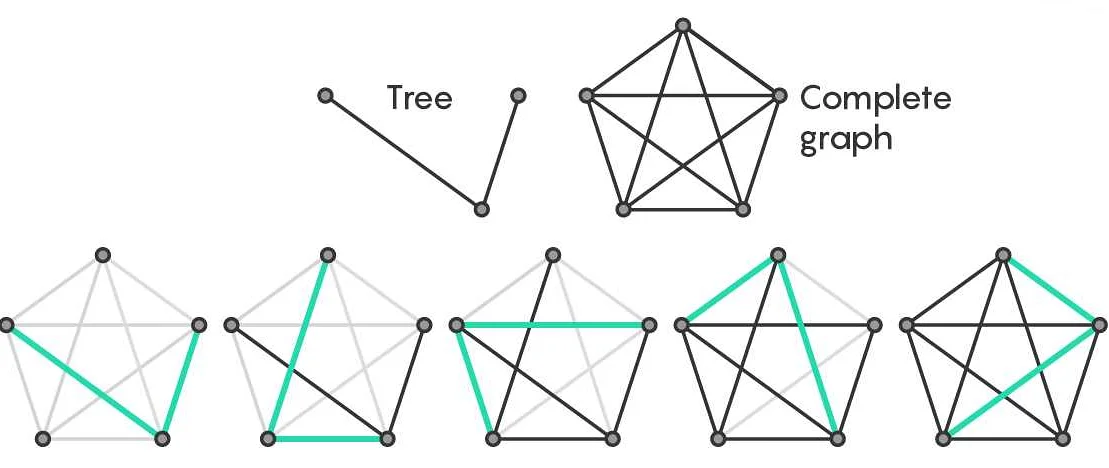
Полный граф в математике – это граф, в котором каждая вершина соединена ребром с каждой другой вершиной. Узнайте, как определить полный граф и какие свойства он имеет.

Полный граф — одна из наиболее изучаемых структур в теории графов, в которой каждая вершина соединена ребрами с каждой другой вершиной. Таким образом, в полном графе каждая пара вершин имеет ребро между ними. Это особенное свойство делает полный граф одним из наиболее интересных объектов изучения в математике.

Одно из ключевых свойств полного графа — его минимальное количество ребер. Для графа с n вершинами, количество ребер в полном графе равно n*(n-1)/2. Это следует из того факта, что каждая вершина соединена с каждой другой ребром, и каждое ребро соединяет пару вершин.

Пример: рассмотрим полный граф с 4 вершинами. В таком графе каждая из 4 вершин соединена с каждой другой ребром. Таким образом, общее количество ребер равно 4*(4-1)/2 = 6.

Полный граф также обладает другими важными свойствами. Например, в полном графе с n вершинами, степень каждой вершины равна n-1, так как каждая вершина связана со всеми остальными вершинами. Кроме того, полный граф — это граф, в котором нет петель (ребер, соединяющих вершину с самой собой) и кратных ребер (несколько ребер, соединяющих одну и ту же пару вершин).

Определение полного графа в математике

Полный граф обозначается символом Kn, где n — количество вершин в графе. Таким образом, полный граф K3 будет иметь три вершины, а полный граф K4 — четыре вершины.

Полный граф является одним из простейших и наиболее изучаемых графов в математике. Он служит основой для многих теоретических и практических исследований в области теории графов, комбинаторики и сетевого анализа.

Свойства полного графа

Полный граф имеет следующие свойства:

Свойство	Описание
Количество ребер	В полном графе Kn количество ребер равно n(n-1)/2.
Степень вершин	Все вершины полного графа имеют одинаковую степень, равную n-1.
Диаметр	Диаметр полного графа Kn равен 1.
Связность	Полный граф является связным графом, то есть любые две его вершины можно соединить ребром.
Планарность	Полный граф Kn непланарен для n ≥ 5.

Эти свойства делают полный граф одной из самых изучаемых и используемых структур в теории графов.

Количество ребер в полном графе

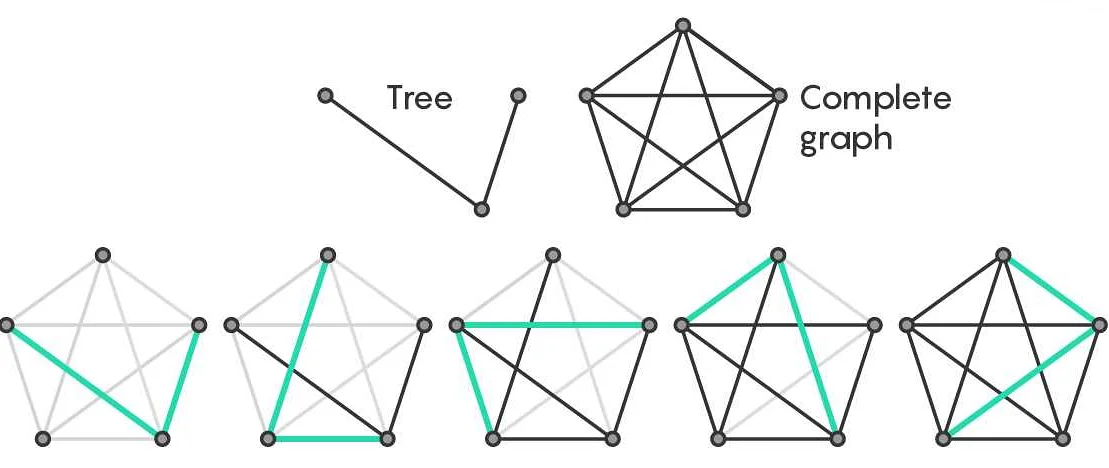
Пусть в полном графе имеется n вершин. Чтобы посчитать количество ребер, нужно знать, что каждая вершина соединена с каждой остальной вершиной. Таким образом, каждая вершина имеет (n-1) ребер. Однако, в результате такого подсчета, каждое ребро будет посчитано дважды (так как каждое ребро соединяет две вершины). Поэтому, чтобы получить количество ребер в полном графе, необходимо поделить полученное значение на 2.

Итак, количество ребер в полном графе с n вершинами можно вычислить по формуле:

Количество ребер = (n * (n — 1)) / 2

Например, в полном графе с 5 вершинами количество ребер будет равно:

Количество ребер = (5 * (5 — 1)) / 2 = 10

Степени вершин в полном графе

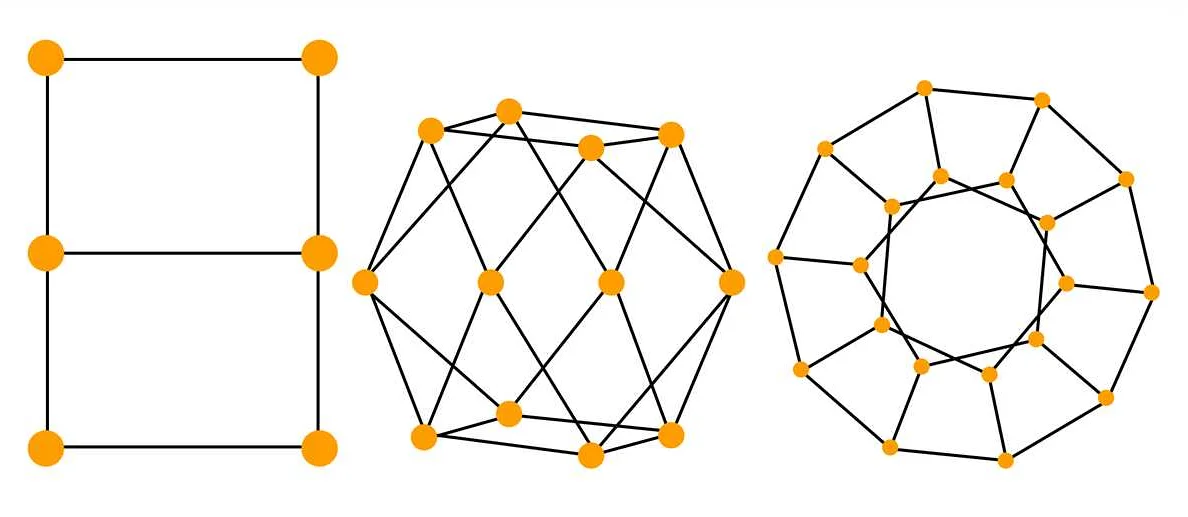
Таким образом, в полном графе с 3 вершинами степень каждой вершины будет равна 2 (3-1=2), в полном графе с 4 вершинами — 3 (4-1=3), и так далее.

Степень вершин в полном графе имеет некоторые интересные свойства:

• В полном графе с нечетным количеством вершин каждая вершина имеет четную степень.
• В полном графе с четным количеством вершин половина вершин имеет четную степень, а другая половина — нечетную.

Эти свойства можно объяснить следующим образом: в полном графе каждая вершина связана с каждой другой вершиной, поэтому каждое ребро добавляет 1 к степени двух вершин. Поскольку каждое ребро имеет две конечные вершины, сумма всех степеней вершин будет равна удвоенному числу ребер. В полном графе с n вершинами имеется n(n-1)/2 ребер, а значит, сумма степеней вершин равна n(n-1). Далее, если количество вершин нечетное, то n(n-1) является четным числом, а значит, каждая вершина имеет четную степень. Если же количество вершин четное, то n(n-1) является нечетным числом, и поэтому половина вершин имеет четную степень, а другая половина — нечетную.

Соединенность полного графа

Соединенность полного графа означает, что между любыми двумя вершинами полного графа существует ребро. Это означает, что любые две вершины можно соединить путем последовательного прохождения через другие вершины полного графа.

Свойство соединенности полного графа делает его особенно интересным и полезным в различных областях, таких как сетевая топология, транспортная логистика, алгоритмы решения задач коммивояжера и многих других.

Соединенность полного графа также имеет важное значение при рассмотрении его связности. Полный граф всегда является связным, так как между любыми двумя его вершинами можно найти путь.

Важно отметить, что полный граф — это простейший пример графа, обладающего свойством полноты и соединенности. В более общем случае существуют другие графы, которые также обладают этими свойствами, однако они не являются полными.

Планарность полного графа

Вопрос о планарности полного графа заключается в том, можно ли изобразить данный граф на плоскости так, чтобы его ребра не пересекались. Если это возможно, то говорят, что полный граф планарный.

Однако, для полного графа pланарность не выполняется при n ≥ 5. Это можно доказать, используя формулу Эйлера для плоских графов: v — e + f = 2, где v — число вершин, e — число ребер, f — число граней (областей, на которые плоский граф делит плоскость). Для полного графа с n вершинами число ребер будет равно C(n, 2) = n(n-1)/2, а число граней будет равно 1. Подставив значения в формулу Эйлера, получим n — n(n-1)/2 + 1 = 2. Решив это уравнение, мы получаем n(n-3)/2 = 0. Из этого следует, что полный граф планарный только для n=1,2,3,4.

Таким образом, полный граф не является планарным для n ≥ 5. Это свойство можно использовать для доказательства непланарности других графов, путем добавления или удаления ребер.

Построение полного графа

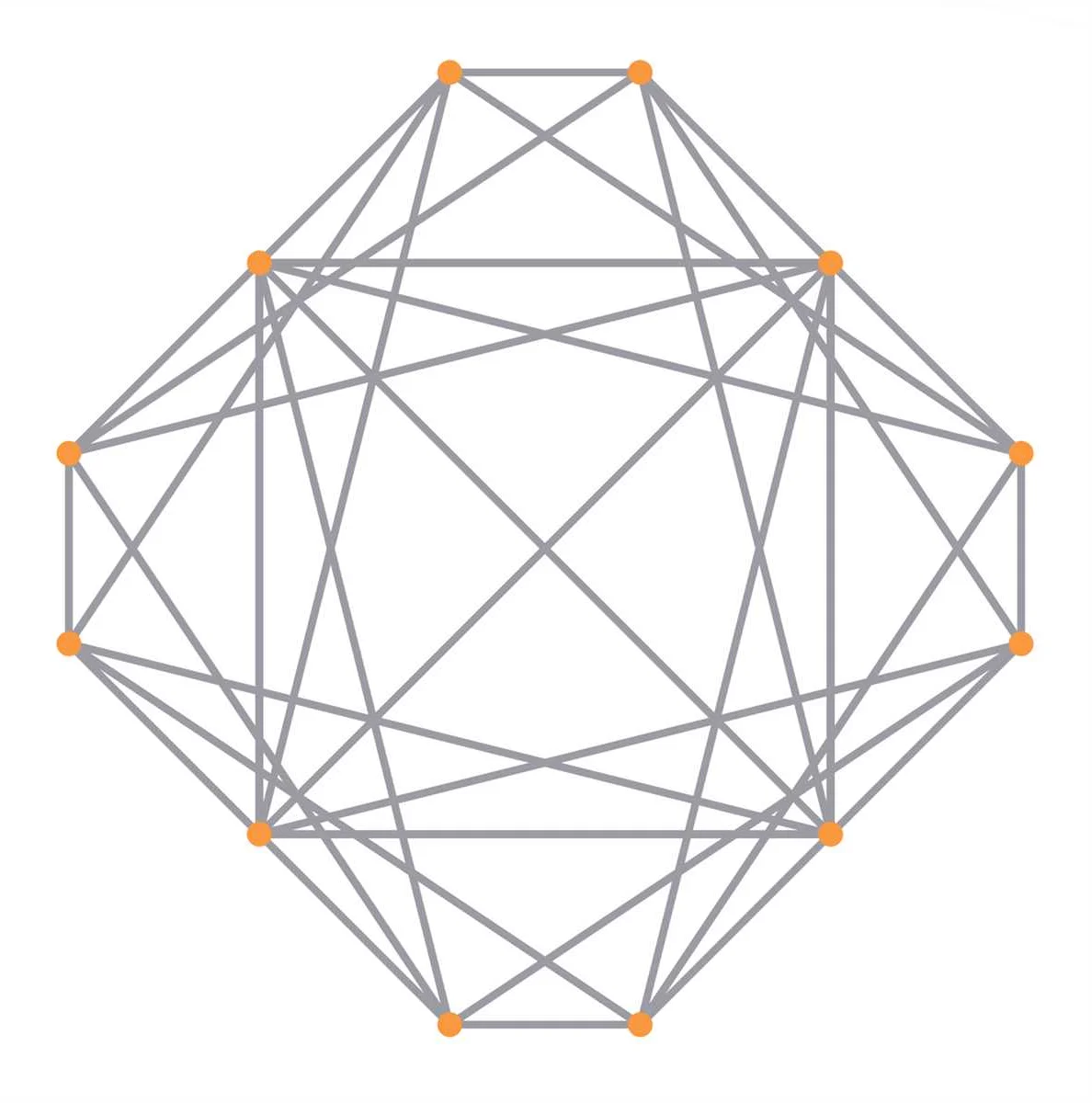
Количество ребер в полном графе можно вычислить по формуле:

Количество ребер = (количество вершин * (количество вершин — 1)) / 2

Например, для полного графа с 5 вершинами количество ребер будет равно: (5 * (5 — 1)) / 2 = 10.

Построить полный граф можно вручную, рисуя ребра между всеми парами вершин. Однако, при большом количестве вершин это может быть затруднительно и требовать значительных усилий и времени. В таких случаях можно использовать специальные программы или алгоритмы для автоматического построения полного графа.

Вопрос-ответ:

Что такое полный граф в математике?

Полный граф — это граф, в котором каждая пара вершин соединена ребром. В полном графе все вершины связаны друг с другом, что делает его одним из наиболее простых и основных объектов изучения в теории графов.

Какие свойства имеет полный граф?

У полного графа есть несколько важных свойств. Во-первых, в полном графе количество ребер равно n(n-1)/2, где n — количество вершин. Во-вторых, полный граф является связным графом, то есть между любыми двумя вершинами существует путь. Кроме того, полный граф является полным двудольным графом, так как его можно разделить на две доли, где все ребра соединяют вершины из разных долей.

Как можно представить полный граф в виде матрицы?

Полный граф можно представить в виде квадратной матрицы с размерностью n x n, где n — количество вершин. Значение элемента матрицы A[i][j] будет равно 1, если между вершинами i и j существует ребро, и 0 в противном случае. Диагональные элементы матрицы всегда равны 0, так как в полном графе нет петель.

Каково общее количество ребер в полном графе с n вершинами?

Общее количество ребер в полном графе с n вершинами равно n(n-1)/2. Это следует из того, что каждая вершина соединена с каждой другой вершиной, и чтобы посчитать количество ребер, нужно подсчитать количество комбинаций из n элементов по 2.

Как можно найти количество ребер в полном графе, если известно количество вершин?

Если известно количество вершин в полном графе, то количество ребер можно вычислить по формуле n(n-1)/2, где n — количество вершин. Например, для полного графа с 5 вершинами, общее количество ребер будет равно 5(5-1)/2 = 10.

Что такое полный граф и как его можно определить?

Полный граф — это граф, в котором каждая вершина соединена ребром с каждой другой вершиной. Он может быть определен как граф с наименьшим количеством вершин, при котором все вершины связаны между собой.

Какие свойства имеет полный граф?

Полный граф имеет несколько свойств. Во-первых, он является полным взвешенным графом, то есть каждое ребро имеет свой вес. Во-вторых, он является полным ориентированным графом, то есть каждая пара вершин связана направленным ребром. В-третьих, полный граф является простым графом, то есть в нем нет петель и кратных ребер. В-четвертых, он является несвязным графом, то есть между любыми двумя вершинами существует путь. В-пятых, полный граф имеет максимальное количество ребер, равное n(n-1)/2, где n — количество вершин.

Применение полного графа в практике

Полные графы имеют широкое применение в математике и практических областях. Вот некоторые примеры использования полных графов:

1. Транспортное планирование: Полные графы используются для моделирования сетей транспортных маршрутов. Например, они могут помочь определить оптимальный маршрут для поставки товаров между различными точками.
2. Социальные сети: Полные графы могут использоваться для анализа и моделирования социальных сетей. Они могут помочь определить связи между людьми и выявить наиболее влиятельных участников.
3. Графические алгоритмы: Полные графы широко используются в графических алгоритмах, таких как алгоритмы обхода графа или алгоритмы поиска кратчайшего пути. Они помогают визуализировать и обрабатывать графическую информацию.
4. Криптография: Полные графы могут использоваться в криптографических алгоритмах, таких как алгоритмы шифрования или аутентификации. Они обеспечивают безопасность и конфиденциальность данных.
5. Биоинформатика: Полные графы используются для моделирования биологических сетей, таких как генные сети или метаболические пути. Они помогают исследовать и понять сложные биологические процессы.

Это лишь некоторые примеры применения полных графов. В действительности, полные графы находят свое применение в широком спектре областей и играют важную роль в решении различных задач.

Видео по теме: