Что такое е в математике производная
Содержимое
- 1 Что такое е в математике производная
- 1.1 Определение производной в математике
- 1.2 Понятие предела функции и его связь с производной
- 1.3 Моменты нахождения производной
- 1.4 Правила дифференцирования
- 1.5 Физический смысл производной
- 1.6 Применение производной в экономике и финансах
- 1.7 Производная в геометрии и физике
- 1.8 Производная и оптимизация функций
- 1.9 Вопрос-ответ:
- 1.10 Видео по теме:
Понятие производной в математике. Е — особая константа, используемая для вычисления производных. Узнайте, как применить е к вычислению производной и как она связана с экспоненциальной функцией.
Производная является одним из ключевых понятий математического анализа. Она позволяет определить скорость изменения функции в каждой ее точке. Производная также используется для нахождения экстремумов функций, исследования поведения графиков и решения различных задач.
Определение производной основывается на понятии предела. Производная функции в точке равна пределу отношения приращения функции к приращению аргумента при стремлении последнего к нулю. Формально, производная функции f(x) в точке x_0 обозначается как f'(x_0) или dy/dx|x=x_0. Это дает нам информацию о том, как функция меняется вблизи данной точки.
Понимание производной играет важную роль во многих областях, таких как физика, экономика и инженерия. Она позволяет анализировать и моделировать изменение различных величин и явлений. Без производной мы не смогли бы понять, как изменяется скорость, ускорение или стоимость товара в зависимости от времени.
Определение производной в математике
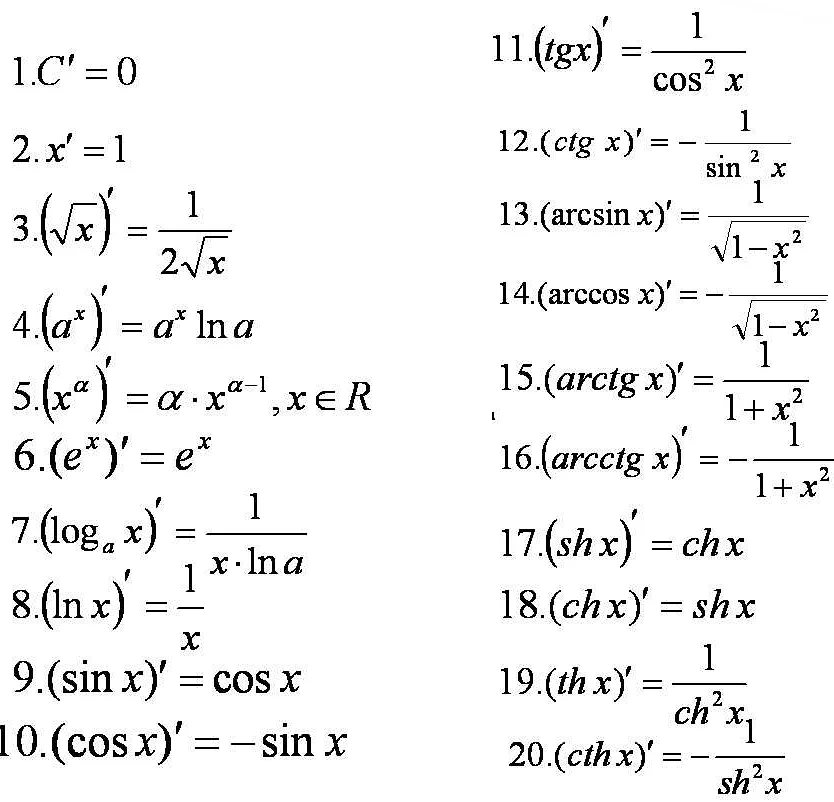
Формально, производная функции f(x) в точке x=a определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю:
f'(a) = limh→0 (f(a+h) — f(a))/h
Это означает, что производная в точке a показывает скорость изменения функции в окрестности этой точки.
Производная функции может быть интерпретирована геометрически как тангенс угла наклона касательной к графику функции в данной точке.
Понятие предела функции и его связь с производной

Предел функции f(x) при x, стремящемся к a, обозначается как:
Предел функцииОпределение
| limx→a f(x) = L | Для любого положительного числа ε существует положительное число δ такое, что для всех x, отличных от a, и удовлетворяющих неравенству 0 < |x — a| < δ, значение функции f(x) отличается от L менее чем на ε. |
Предел функции позволяет вычислить производную функции в точке a. Если предел функции при x, стремящемся к a, существует, то говорят, что функция f(x) дифференцируема в точке a, и производная функции в этой точке определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю:
f'(a) = limh→0 (f(a+h) — f(a))/h
Таким образом, понятие предела функции является основой для определения производной функции и позволяет изучать ее свойства и поведение в окрестности определенной точки.
Моменты нахождения производной

Для нахождения производной функции необходимо следовать определенным шагам:
- Выбрать функцию, производную которой необходимо найти.
- Определить переменную, по которой будет осуществляться дифференцирование.
- Применить правила дифференцирования для данной функции.
- Выразить полученное выражение через исходную переменную.
Как только производная функции найдена, можно использовать ее для решения различных задач. Например:
- Найти касательную к графику функции в определенной точке.
- Определить экстремумы функции — точки, в которых производная равна нулю или не существует.
- Исследовать поведение функции на отрезке — определить, где она возрастает, убывает или имеет точки перегиба.
Моменты нахождения производной являются важными для понимания и применения математических концепций и решения различных задач.
Правила дифференцирования
Существуют несколько правил, которые позволяют дифференцировать различные типы функций. Некоторые из них:
- Правило линейности: если функция f(x) и функция g(x) дифференцируемы в точке x, то их сумма (или разность) их производных также дифференцируема в этой точке.
- Правило произведения: если функции f(x) и g(x) дифференцируемы в точке x, то их произведение также дифференцируемо в этой точке, и производная равна произведению производных.
- Правило частного: если функции f(x) и g(x) дифференцируемы в точке x, и g(x) не равно нулю в этой точке, то их частное также дифференцируемо в этой точке, и производная равна частному производных.
- Правило композиции: если функция f(x) дифференцируема в точке x, а функция g(x) дифференцируема в точке f(x), то их композиция также дифференцируема в точке x, и производная равна произведению производной внешней функции на производную внутренней функции.
Это лишь некоторые из основных правил дифференцирования, которые широко применяются при решении математических задач. Знание этих правил позволяет анализировать функции и находить их производные с помощью более простых операций.
Физический смысл производной

Например, скорость является производной по времени относительного перемещения. Если задан график перемещения тела в зависимости от времени, то производная этой функции в конкретный момент времени показывает скорость тела в этот момент. То есть, производная позволяет нам определить, как быстро меняется положение тела в определенный момент времени.
Также производная может интерпретироваться как скорость изменения одной физической величины относительно другой. Например, если задан график температуры в зависимости от времени, то производная этой функции в конкретный момент времени будет означать скорость изменения температуры в этот момент. То есть, производная позволяет нам определить, насколько быстро изменяется температура в определенный момент времени.
Таким образом, производная имеет физический смысл измерения скорости изменения величин в различных физических задачах. Она позволяет нам анализировать и понимать, как меняются физические величины в зависимости от других факторов и дает нам инструменты для решения задач, связанных с физикой.
Применение производной в экономике и финансах

В экономике производные используются для изучения законов спроса и предложения. Например, производная спроса показывает, как изменится количество товара, при изменении его цены. Эта информация позволяет компаниям принимать решения о ценообразовании и оптимальном уровне производства.
Производные также применяются для анализа рыночной конкуренции. Изучение производных позволяет определить, как изменится прибыль компании при изменении объема производства или цены товара. Это позволяет компаниям прогнозировать результаты своей деятельности и принимать управленческие решения.
В финансах производные используются для анализа доходности и рисков различных инвестиционных инструментов. Например, производная цены акции позволяет определить, как изменится доходность инвестиции при изменении цены акции. Это помогает инвесторам принимать решения о покупке или продаже акций.
Производные также применяются для анализа финансовых рынков и разработки финансовых моделей. Изучение производных позволяет определить, как изменится цена опциона или фьючерсного контракта при изменении цены базового актива. Это позволяет трейдерам прогнозировать рыночные тенденции и принимать решения о покупке или продаже финансовых инструментов.
Таким образом, применение производной в экономике и финансах позволяет анализировать изменения величин и принимать обоснованные решения. Это важный инструмент для оптимизации бизнес-процессов и инвестиционной деятельности.
Производная в геометрии и физике

В геометрии производная используется для определения наклона кривой в данной точке. Например, в оптике производная позволяет определить угол падения и отражения света на поверхности. В механике производная позволяет определить скорость и ускорение тела в движении.
В физике производная имеет особое значение. Она позволяет определить мгновенную скорость и ускорение объекта в данной точке его траектории. Также производная используется для определения изменения физических величин во времени, например, изменение температуры в зависимости от времени или изменение электрического тока в цепи.
Производная также широко применяется в численных методах решения задач. Она позволяет аппроксимировать сложные функции и упрощать математические выражения для проведения различных расчетов.
Таким образом, производная является важным инструментом в геометрии и физике, позволяющим определить наклон, скорость, ускорение и изменение различных физических величин.
Производная и оптимизация функций
Оптимизация функций заключается в поиске экстремумов – точек, в которых функция принимает наибольшее или наименьшее значение. Производная функции позволяет найти такие точки, исследовать их поведение и определить, является ли эта точка экстремумом. Например, если производная функции положительна в точке, то это может говорить о том, что функция имеет локальный минимум в этой точке.
Для оптимизации функций широко используются методы дифференциального исчисления. Они позволяют находить производные функций, исследовать их свойства и находить экстремумы. Это особенно полезно в задачах оптимизации, где требуется найти наилучшее решение.
Производная функции является мощным инструментом в оптимизации и позволяет находить локальные и глобальные минимумы и максимумы функций. Она позволяет определить, где функция достигает наибольшего или наименьшего значения, что помогает улучшить эффективность систем, увеличить прибыль, снизить затраты или достичь других поставленных целей.
Вопрос-ответ:
Что такое производная в математике?
Производная в математике является одним из основных понятий дифференциального исчисления. Она определяет, как изменяется функция в каждой точке своей области определения.
Каким образом можно определить производную функции?
Для определения производной функции необходимо вычислить предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Каков смысл производной функции?
Смысл производной функции заключается в определении скорости изменения значения функции по сравнению с изменением её аргумента.
Какие свойства имеет производная функции?
Производная функции обладает несколькими свойствами, такими как линейность, правила дифференцирования сложных функций, правило Лейбница для произведения функций, правило дифференцирования суммы функций, и другие.
Какую роль играет производная функции в математике и других науках?
Производная функции играет важную роль в математике и других науках. Она позволяет исследовать поведение функций, находить экстремумы, определять скорость изменения величин и многое другое. Без производных функций сложно представить себе современную математику и её применение в реальных задачах.
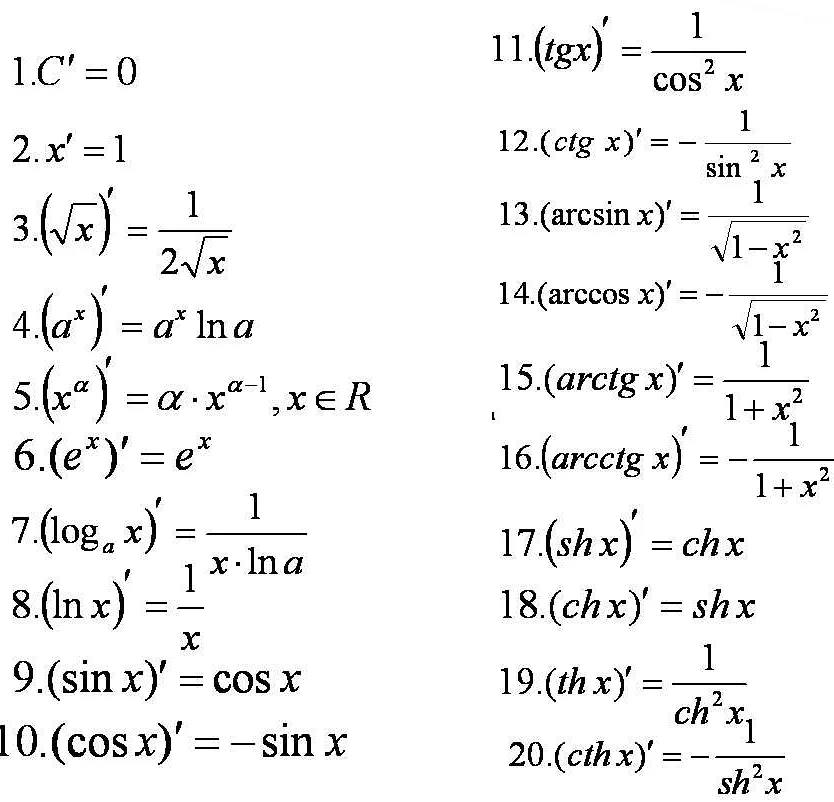

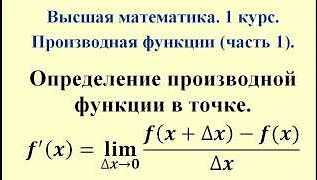


Статья очень полезная и информативная! Я всегда хотела разобраться в том, что такое производная в математике. Автор прекрасно объяснил основные понятия и дал четкое определение. Теперь я понимаю, что производная — это скорость изменения функции в определенной точке. Это очень важно для понимания того, как функции работают и как они могут быть использованы в реальной жизни. Статья была написана простым и доступным языком, что позволило мне легко усвоить материал. Теперь я уверена, что смогу успешно применять производную в своих дальнейших математических исследованиях. Большое спасибо автору за такую полезную и интересную статью!
Производная в математике – это величина, которая показывает, как изменяется функция в зависимости от изменения ее аргумента. Это очень важное понятие, которое помогает нам анализировать различные процессы и явления в нашей жизни. Ведь многие вещи в окружающем мире могут быть представлены в виде функций, и знание их производных позволяет нам понять, как они меняются со временем. На практике это может быть полезно, например, при определении скорости движения тела, при анализе роста популяции или при изучении экономических процессов. Зная производную функции, мы можем определить, какая скорость изменения происходит в определенный момент времени или при определенном значении аргумента. Важно отметить, что производная может быть положительной или отрицательной, что указывает на направление изменения функции. Если производная положительна, это означает, что функция возрастает, а если она отрицательна, то функция убывает. Таким образом, производная – это мощный инструмент, который помогает нам понять и анализировать различные явления в математике и реальном мире. Она является основой для многих других понятий и методов в математике и науке в целом.