Что такое прообраз в математике
Содержимое
Прообраз в математике — это понятие, которое используется для описания отношения между элементами двух множеств. Он представляет собой множество всех элементов, которые являются образами определенного элемента из другого множества по заданному отображению. Узнайте, как определить прообраз и для чего он используется в математических вычислениях.
В математике прообраз — это понятие, которое связано с отображениями и функциями. Прообразом элемента является множество всех таких элементов, которые в результате отображения переходят в данный элемент. То есть, прообраз — это все значения, которые принимает функция при применении к данному элементу.
Понятие прообраза в математике встречается в различных областях, таких как алгебра, геометрия, теория множеств и другие. Оно позволяет описывать и исследовать отображения и функции, определяя их свойства и взаимосвязи между элементами.
Примером прообраза может служить функция f(x) = x^2. Если взять произвольный элемент 4, то его прообразом будут числа 2 и -2, так как при подстановке этих значений в функцию f(x) получаем результат 4. То есть, прообразом элемента 4 являются все значения, которые при подстановке в функцию дают результат 4.
Таким образом, понятие прообраза в математике играет важную роль при изучении отображений и функций, позволяя описывать их свойства и взаимосвязи между элементами. Оно помогает различным областям математики решать задачи и проводить исследования, а также находить применение в реальной жизни.
Понятие прообраза в математике
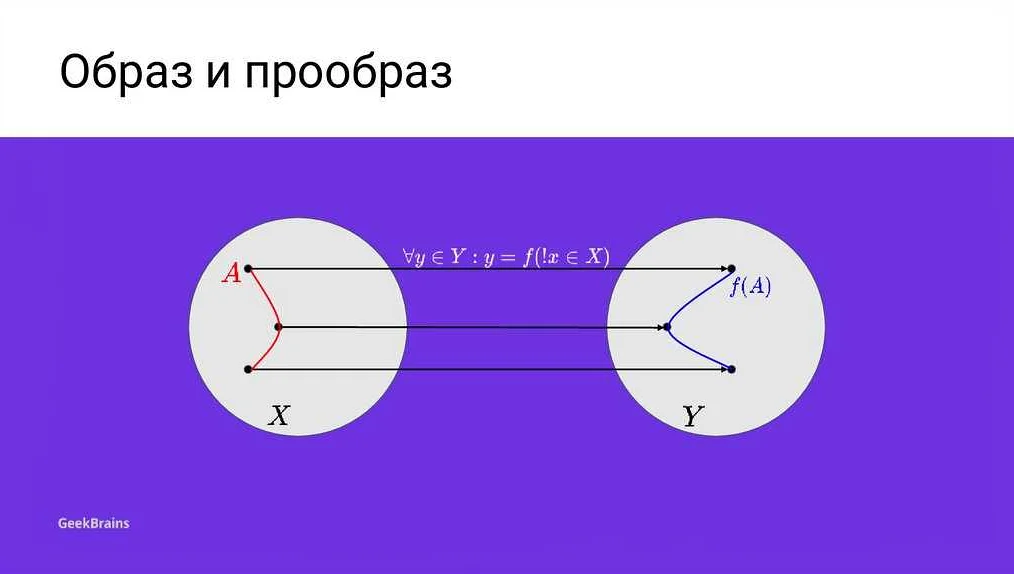
Пусть дано отображение f из множества A в множество B. Тогда для произвольного элемента b из множества B прообразом элемента b относительно отображения f называется множество всех элементов из множества A, которые отображаются в элемент b. Прообраз обозначается как f-1(b) или f-1{b}.
Простым примером может служить отображение функции f(x) = x2 из множества действительных чисел в себя. Если взять элемент b = 4, то прообразом будет множество {-2, 2}. Это связано с тем, что отображение f превращает как положительное, так и отрицательное значение в квадратное значение 4.
Видео по теме:
Определение прообраза
Пусть даны два множества A и B, и существует отношение f, которое связывает элементы из множества A с элементами из множества B. Если b — это элемент из множества B, то прообразом этого элемента будет множество всех элементов a из множества A, таких что f(a) = b.
Прообраз можно также определить как обратную функцию к функции f. Если f: A → B, то обратная функция f-1: B → A определяется следующим образом: для каждого b из множества B, f-1(b) — это прообраз элемента b.
Прообразы играют важную роль в различных областях математики, таких как теория множеств, алгебра, топология и другие. Они позволяют анализировать и описывать отношения между элементами множеств и строить более сложные структуры на их основе.
Примеры прообразов
Вот несколько примеров прообразов:
- Пусть есть функция f(x) = x^2. Если мы рассматриваем множество действительных чисел ℝ и выбираем элемент 4, то прообразом этого элемента будет {-2, 2}, так как f(-2) = 4 и f(2) = 4.
- Рассмотрим функцию g(x) = 2x + 3. Если мы выбираем элемент 7 из множества целых чисел ℤ, то прообразом этого элемента будет {2}, так как g(2) = 7.
- Пусть есть отображение h: {a, b, c} → {1, 2, 3} такое, что h(a) = 1, h(b) = 2 и h(c) = 3. Если мы рассматриваем элемент 2 из множества {1, 2, 3}, то прообразом этого элемента будет {b}, так как h(b) = 2.
Во всех этих примерах прообразом является множество элементов, которые при отображении соответствуют выбранному элементу из образа.
Вопрос-ответ:
Что такое прообраз в математике?
В математике прообраз — это понятие, которое используется в теории множеств и отображений. Прообраз отображения f из множества B в множество A — это такое подмножество множества B, все элементы которого переходят в множество A при применении отображения f.
Какой геометрический пример можно привести для прообраза?
Представим, что у нас есть отображение f, которое берет каждую точку окружности и отображает ее на соответствующую точку на плоскости. Тогда прообраз этого отображения будет состоять из всех точек окружности, которые переходят в определенную точку на плоскости.
Как можно определить прообраз в математике?
Прообраз можно определить как обратную функцию к отображению f. Для каждого элемента b из множества B прообраз f^-1(b) — это множество всех элементов из множества A, которые переходят в b при применении отображения f.
Как прообраз связан с понятием образа?
Прообраз и образ — это взаимосвязанные понятия. Образ отображения — это множество всех элементов, в которые переходят элементы из исходного множества при применении отображения. Прообраз же — это множество всех элементов, которые переходят в определенный элемент образа.
Можно ли привести пример прообраза в математике?
Да, конечно! Рассмотрим отображение f(x) = x^2. Если мы возьмем множество B, состоящее из элементов {1, 4, 9}, то прообразом этого множества будет множество A, состоящее из элементов {-1, 1, -2, 2, -3, 3}, так как при применении отображения f эти элементы переходят в элементы множества B.
Что такое прообраз в математике?
Прообраз — это понятие, которое используется в математике для описания отображения между двумя множествами. Прообразом элемента из целевого множества является множество всех элементов из исходного множества, которые по отображению переходят в данный элемент.
Свойства прообраза
1. Уникальность прообраза:
Каждому элементу изображения соответствует только один прообраз. Это означает, что если два разных элемента имеют одинаковый образ, то их прообразы также будут одинаковыми.
2. Существование прообраза:
Для каждого элемента изображения существует прообраз. То есть для любого элемента изображения можно найти элемент, который отображается в этот образ.
3. Отношение инверсии:
Если элемент A является прообразом элемента B, то элемент B является образом элемента A. Это свойство позволяет устанавливать взаимно-однозначное соответствие между элементами и их прообразами.
4. Зависимость от отображения:
Прообраз зависит от конкретного отображения. Для одного отображения прообраз может быть определен, а для другого — нет. Это значит, что прообраз не является абсолютным понятием, а зависит от контекста и использования.
Все эти свойства помогают понять и использовать прообраз в математике. Они позволяют установить соответствие между элементами и их прообразами, а также определить, существует ли прообраз для конкретного элемента изображения.
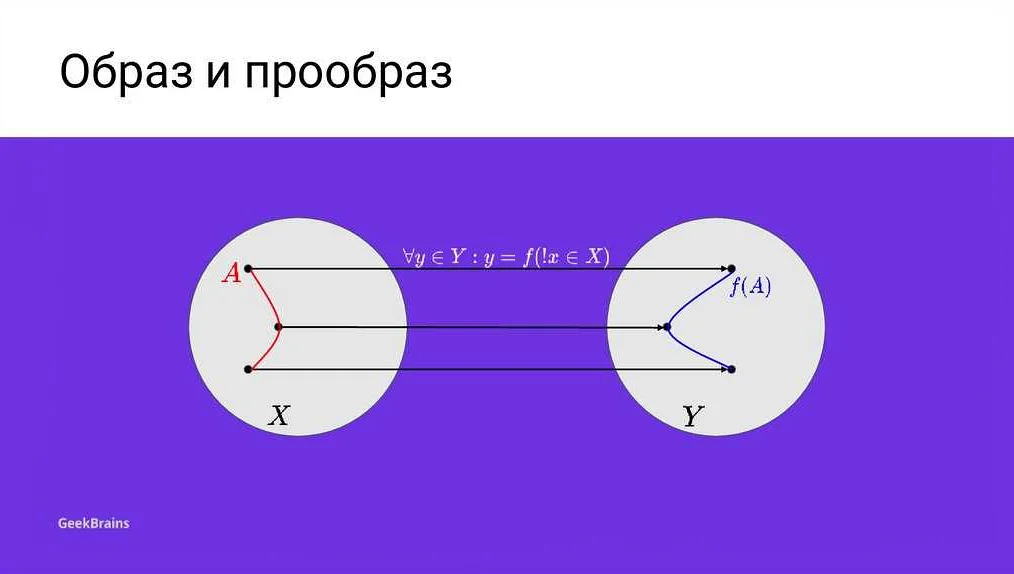
Прообраз и образ

Пусть имеются два множества A и B, и задано отображение f: A → B. Тогда для произвольного элемента y из множества B его прообразом называется множество всех элементов из множества A, которые при отображении f переходят в y. Прообраз обозначается как f^(-1)(y) или f^(-1){y}.
Образом элемента x из множества A называется элемент y из множества B, в который он переходит при отображении f. Образ обозначается как f(x).
Примеры использования прообраза и образа:
- Пусть A = {1, 2, 3, 4}, B = {a, b, c, d}, и отображение f задано следующим образом: f(1) = a, f(2) = b, f(3) = b, f(4) = c. Тогда прообразом элемента b будет множество {2, 3}, а образом элемента 4 будет элемент c.
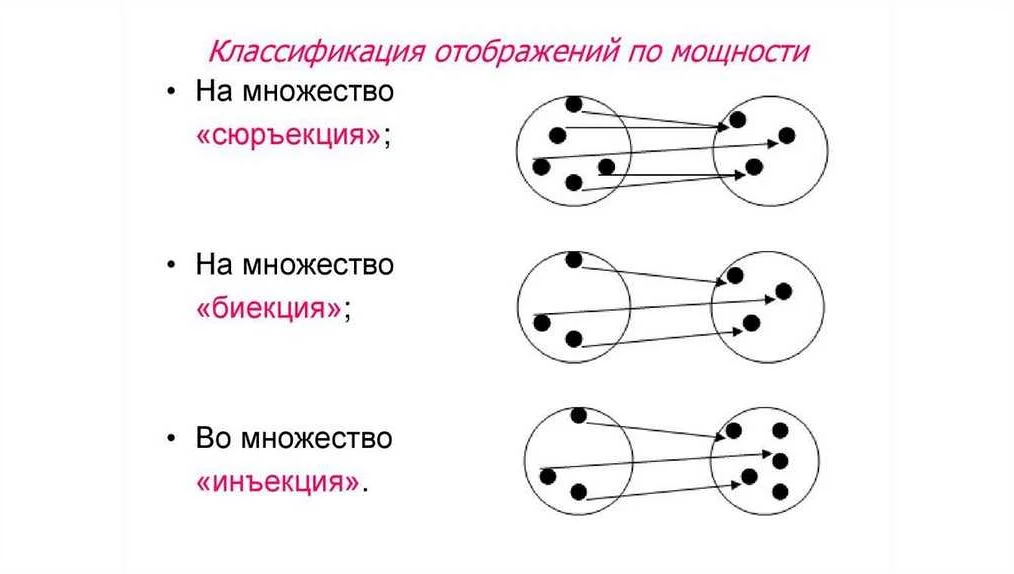
- В алгебре рассматриваются отображения, которые обладают свойством обратимости, то есть для каждого элемента из множества B существует единственный прообраз в множестве A. Такие отображения называются биекциями.
- В теории вероятности прообразы используются для определения вероятности событий. Если задано вероятностное пространство (Ω, F, P) и событие B, то его прообразом будет множество всех элементов из Ω, которые переходят в B при отображении P.
Таким образом, понятия прообраза и образа играют важную роль в математике и находят применение в различных областях.
Прообраз в функции
Прообраз в функции можно определить следующим образом: если есть функция f, определенная на множестве A и имеющая область значений B, то для любого элемента b из множества B можно найти такой элемент a из множества A, что f(a) = b. Такой элемент a называется прообразом элемента b.
Прообраз может быть пустым множеством, если не существует такого элемента a, который бы при подстановке в функцию f давал значение b. Однако в большинстве случаев прообраз является непустым множеством.
Прообраз в функции может быть использован для нахождения всех возможных значений, которые могут быть получены при заданных входных данных. Это позволяет более полно исследовать свойства функции и определить ее обратную функцию.
Примером использования прообраза в функции может служить функция f(x) = x^2. Если множество A является множеством всех вещественных чисел, то прообразом для числа 4 будет множество {-2, 2}, так как при подстановке этих значений в функцию получается результат 4.
Прообраз множества
Для более формального определения прообраза, пусть задано отображение f: A → B, где A и B — два множества. Если y ∈ B, то прообразом элемента y называется множество всех x ∈ A, таких что f(x) = y. Прообраз обозначается как f^(-1)(y) или f^(-1){y}.
Примером использования прообраза может служить отображение f: ℝ → ℝ, заданное формулой f(x) = x^2. Если мы хотим найти прообраз элемента y = 4, то нужно решить уравнение x^2 = 4. В данном случае прообразом элемента 4 являются два числа: x = -2 и x = 2. Таким образом, прообразом числа 4 при данном отображении является множество {-2, 2}.
Прообраз числа
Для более ясного объяснения понятия прообраза числа, рассмотрим следующий пример. Пусть у нас есть функция f, которая отображает множество X на множество Y. Пусть число y принадлежит множеству Y. Прообраз числа y, обозначаемый f-1(y), определяется как множество всех элементов x, для которых f(x) = y.
Например, пусть у нас есть функция f(x) = x2, которая отображает множество всех действительных чисел на себя. Если мы хотим найти прообраз числа 4, то нужно решить уравнение f(x) = 4. В данном случае, прообразом числа 4 будет множество {-2, 2}, так как f(-2) = 4 и f(2) = 4.
Множество XМножество YФункция f(x)
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
В таблице выше показан пример отображения множества X на множество Y с помощью функции f(x) = x2. Как видно, число 4 имеет прообразы {-2, 2}, число 1 имеет прообраз 1, а число 9 имеет прообраз 3.



Я всегда интересовался математикой, но понятие прообраза было для меня какой-то загадкой. К счастью, эта статья помогла мне разобраться. Прообраз — это такая функция, которая связывает элементы множества, называемого областью значений, с элементами другого множества, называемого областью определения. Прообраз можно представить как «обратную» функцию, которая позволяет нам найти исходные элементы по заданным значениям. Например, представим, что у нас есть функция f(x) = x^2. Если мы хотим найти прообраз числа 4, то должны решить уравнение x^2 = 4. Решением этого уравнения являются числа -2 и 2, то есть их прообразом является число 4. Другой пример — функция f(x) = 2x. Если мы хотим найти прообраз числа 6, то должны решить уравнение 2x = 6. Решением будет число 3, то есть его прообразом является число 6. Важно понимать, что не для всех значений из области значений существуют прообразы. Например, в функции f(x) = x^2 не существует прообраза для отрицательных чисел, так как квадрат отрицательного числа будет положительным. Теперь я лучше понимаю, что такое прообраз и как его находить. Это дает мне возможность лучше разбираться в математических задачах и анализировать функции.
Статья очень понятно и доступно объясняет понятие прообраза в математике. Я всегда был немного запутан в этой теме, но после прочтения статьи мне стало все ясно. Прообраз — это множество всех элементов, которые переходят в заданный элемент при применении функции. Пример с картиной очень наглядно показывает, как работает это понятие. Если функция представляет собой процесс превращения изображения в черно-белую версию, то прообраз будет состоять из всех цветных пикселей, которые были на изначальном изображении. Статья помогла мне лучше понять математический термин и применение его в реальной жизни. Спасибо автору за подробное объяснение!
Прообраз в математике — это понятие, которое встречается в теории множеств и отображений. Он используется для описания отношения между элементами двух множеств. Прообраз элемента из одного множества — это множество всех элементов другого множества, которые при отображении попадают в данный элемент. К примеру, представим себе два множества: множество A — {1, 2, 3, 4, 5}, и множество B — {a, b, c, d, e}. Пусть есть отображение f, которое сопоставляет элементам из множества B элементы из множества A следующим образом: f(a) = 1, f(b) = 2, f(c) = 1, f(d) = 3, f(e) = 1. Тогда прообразом элемента 1 из множества A будет множество {a, c, e}, так как именно эти элементы при отображении f попадают в элемент 1. Аналогично, прообразом элемента 2 будет множество {b}, прообразом элемента 3 — множество {d}. Таким образом, понятие прообраза позволяет нам анализировать отношения между элементами множеств и их отображениями. Оно находит применение в различных областях математики, таких как алгебра, топология и дискретная математика.