Что такое инъекция в математике

Инъекция в математике — это функция, которая сопоставляет каждому элементу из одного множества элемент из другого множества таким образом, что каждому элементу из первого множества сопоставляется только один элемент из второго множества. В данной статье рассматривается понятие инъекции в математике, ее свойства и примеры применения.

Инъекция в математике — это ключевой термин, который описывает свойство отображений между множествами. Оно используется для определения отношений между элементами двух множеств и позволяет нам понять, какие элементы имеют однозначные соответствия между собой.

В математике инъекция также называется «вложение» или «внедрение». В отличие от сюръекции, когда каждому элементу одного множества соответствует хотя бы один элемент другого множества, инъекция гарантирует, что каждому элементу одного множества соответствует не более одного элемента другого множества.

Например, давайте рассмотрим отображение f: A -> B. Если для каждого элемента a из множества A существует только один элемент b из множества B, такой что f(a) = b, то отображение f является инъекцией.

Инъекции имеют много полезных свойств и применений в математике и компьютерных науках. Они широко используются в теории графов, криптографии, алгоритмах сжатия данных и многих других областях. Понимание инъекций помогает улучшить эффективность алгоритмов и предотвратить ошибки в обработке данных.

В этой статье мы рассмотрим более подробно определение инъекции, приведем примеры инъективных отображений и рассмотрим основные свойства этого важного понятия в математике.

Определение инъекции

Формально, отображение f: A → B называется инъекцией, если для каждого элемента x и y из множества A выполняется условие:

• Если f(x) = f(y), то x = y.

Иными словами, каждому элементу из множества A соответствует только один элемент из множества B. Если для двух различных элементов x и y из A значение f(x) = f(y), то это противоречит определению инъекции.

Инъективные отображения являются важным понятием в математике и широко применяются в различных областях, включая теорию множеств, анализ, алгебру и дискретную математику.

Видео по теме:

Примеры инъекций

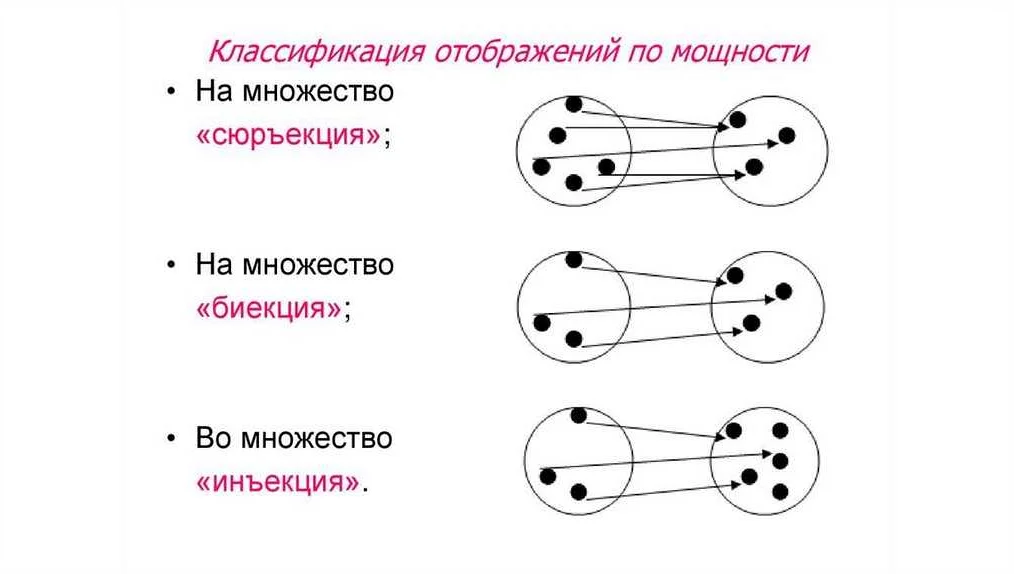
1. Инъекция в функции

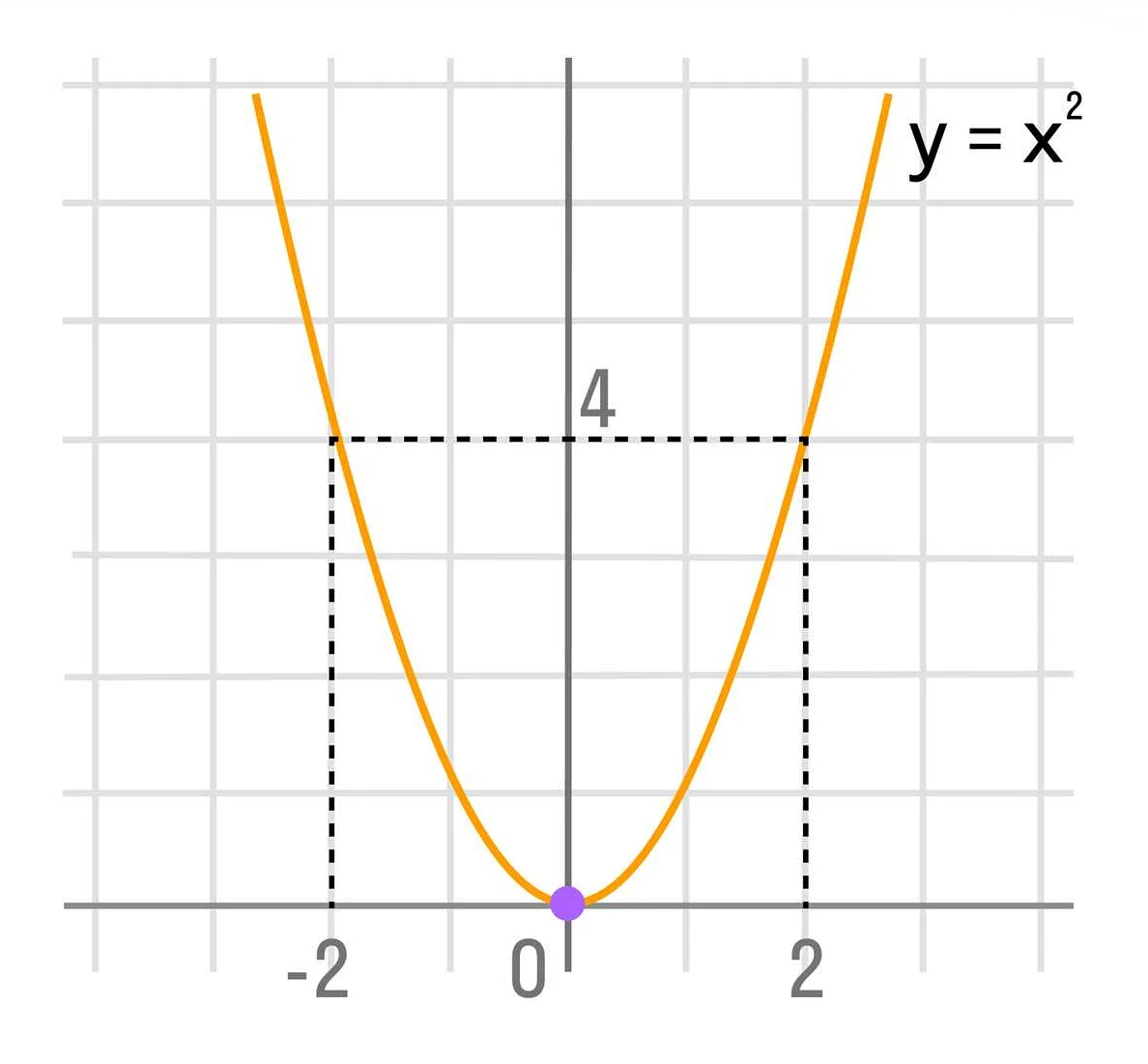
Рассмотрим функцию f(x) = x^2. Эта функция является инъекцией, так как каждому значению x соответствует уникальное значение x^2. Например, f(2) = 4 и f(3) = 9. Значит, функция f(x) = x^2 является инъекцией.

2. Инъекция в множества

Рассмотрим множества A = {1, 2, 3} и B = {a, b, c}. Определим функцию f, которая сопоставляет каждому элементу множества A элемент множества B. Например, f(1) = a, f(2) = b и f(3) = c. В данном случае, функция f является инъекцией, так как каждому элементу множества A соответствует уникальный элемент множества B.

3. Инъекция в числовую прямую

Рассмотрим числовую прямую. Определим функцию f(x) = 2x. Также определим функцию g(x) = x + 1. Функция f является инъекцией, так как каждому числу x соответствует уникальное число 2x. Например, f(1) = 2 и f(2) = 4. Функция g также является инъекцией, так как каждому числу x соответствует уникальное число x + 1. Например, g(1) = 2 и g(2) = 3. Значит, функции f(x) = 2x и g(x) = x + 1 являются инъекциями на числовой прямой.

4. Инъекция в множество строк

Рассмотрим множество строк. Определим функцию f, которая преобразует каждую строку в ее длину. Например, f(«abc») = 3 и f(«hello») = 5. Функция f является инъекцией, так как каждой строке соответствует уникальное число — ее длина.

5. Инъекция в множество дробных чисел

Рассмотрим множество дробных чисел. Определим функцию f(x) = 2x. Также определим функцию g(x) = x/2. Функция f является инъекцией, так как каждому числу x соответствует уникальное число 2x. Например, f(1/2) = 1 и f(1) = 2. Функция g также является инъекцией, так как каждому числу x соответствует уникальное число x/2. Например, g(2) = 1 и g(4) = 2. Значит, функции f(x) = 2x и g(x) = x/2 являются инъекциями на множестве дробных чисел.

Свойства инъекций

СвойствоОпределение

Однозначное соответствие	Каждому элементу X соответствует только один элемент Y
Отсутствие дубликатов	Все элементы Y различны
Сохранение порядка	Порядок элементов X сохраняется в элементах Y
Инверсия невозможна	Нельзя получить тот же элемент X из двух разных элементов Y

Эти свойства позволяют использовать инъекции для установления соответствия между различными объектами или областями. Они широко применяются в различных областях, включая теорию графов, криптографию и компьютерные науки.

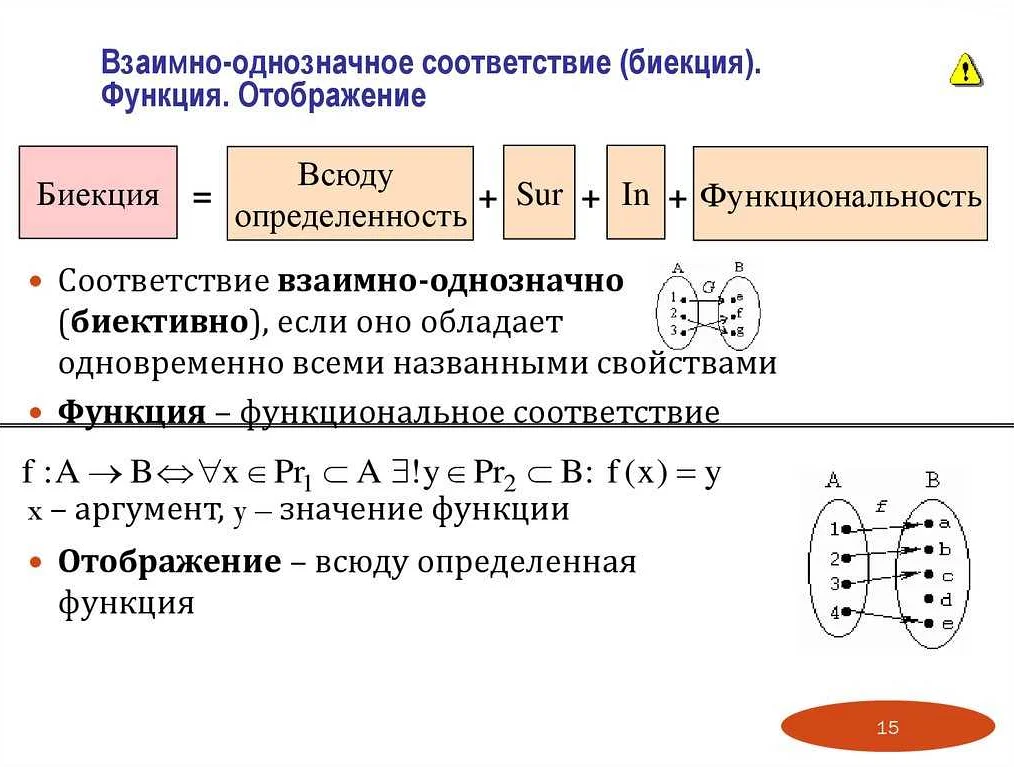
Инъекции и биекции

Биекция — это особый тип отображения, которое является одновременно и инъекцией, и сюръекцией. То есть, каждому элементу из одного множества сопоставляется уникальный элемент из другого множества, и при этом все элементы из второго множества имеют свои прообразы в первом множестве.

Инъекции и биекции являются важными понятиями в теории множеств и алгебре. Они позволяют описать отношения между элементами множеств и определить их свойства.

Примеры инъекций и биекций можно найти в различных областях математики. Например, в анализе и геометрии, инъекции часто используются для описания отображений между пространствами, где каждая точка имеет уникальный прообраз. Биекции могут использоваться для установления соответствия между различными объектами или для построения взаимно однозначного соответствия между двумя множествами.

Свойства инъекций и биекций также являются важными для понимания структуры множеств. Например, инъекция может использоваться для определения размера множества, тогда как биекция позволяет установить равномощность двух множеств.

В заключение, инъекции и биекции играют важную роль в математике и имеют множество применений. Понимание этих понятий помогает в изучении различных областей математики и строительстве формальных моделей.

Инъекции и сюръекции

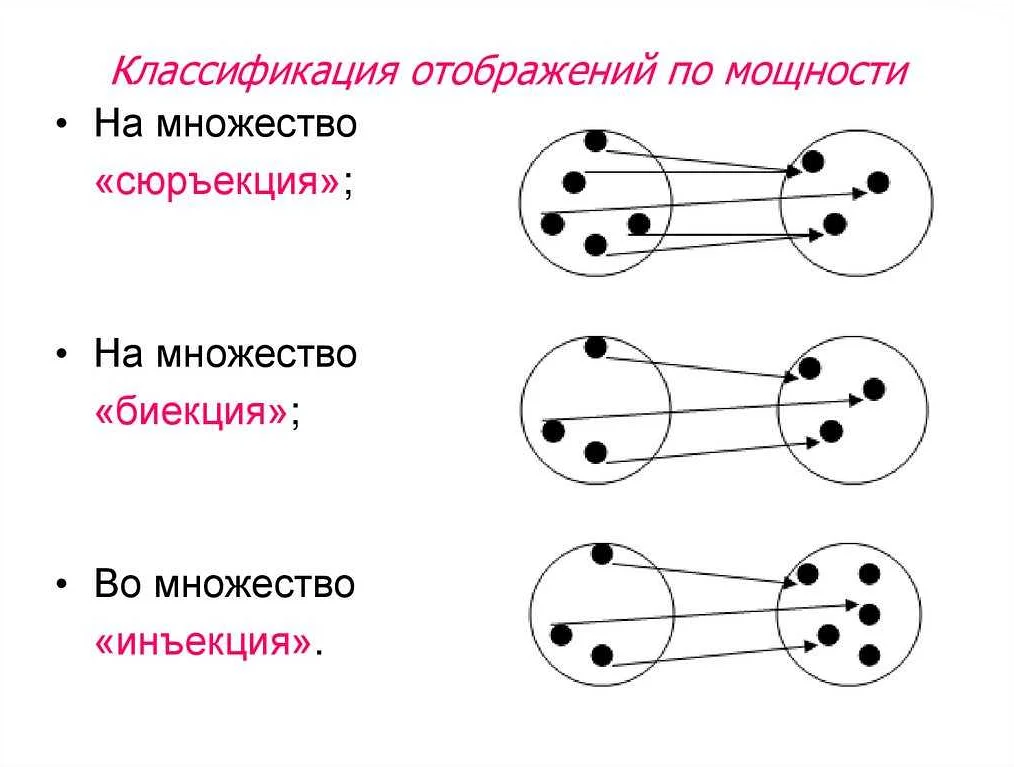
Инъекция — это функция, которая отображает каждый элемент исходного множества в уникальный элемент целевого множества. Другими словами, каждому элементу исходного множества соответствует только один элемент целевого множества. Если функция является инъекцией, то она называется инъективной или однозначной.

Сюръекция — это функция, которая отображает каждый элемент исходного множества на элемент целевого множества. Другими словами, каждый элемент целевого множества имеет соответствующий элемент в исходном множестве. Если функция является сюръекцией, то она называется сюръективной или находит все значения.

Инъекция и сюръекция являются обратными понятиями друг другу. Функция может быть инъекцией, сюръекцией или обеими одновременно. Если функция является и инъекцией, и сюръекцией, то она называется биекцией или взаимно однозначным отображением.

Инъекции и сюръекции широко используются в различных областях математики, включая анализ, алгебру, теорию чисел и дискретную математику. Они играют важную роль в установлении соответствия и отношений между множествами.

Практическое применение инъекций

Инъекции находят широкое применение в различных областях, где требуется обработка и анализ данных. Вот несколько примеров, где использование инъекций может быть полезным:

1. Базы данных

Инъекции могут использоваться для доступа и манипуляции данными в базах данных. Например, инъекция SQL позволяет злоумышленнику выполнить вредоносные SQL-запросы, что может привести к утечке данных или повреждению базы данных.

2. Веб-разработка

Инъекции могут использоваться для атак на веб-приложения. Например, инъекция кода может позволить злоумышленнику выполнить произвольный код на сервере и получить доступ к защищенным данным.

3. Компьютерная безопасность

Инъекции широко используются в области компьютерной безопасности для тестирования уязвимостей систем. Например, инъекция команд может использоваться для проверки наличия уязвимости в системе, которая позволяет выполнить произвольные команды на удаленном сервере.

4. Математическое моделирование

Инъекции могут быть применены для моделирования сложных математических задач. Например, инъекция выражений может использоваться для решения уравнений, оптимизации функций или анализа данных.

Все эти примеры демонстрируют, что инъекции могут быть полезным инструментом, но также могут представлять серьезную угрозу безопасности. Поэтому важно принимать меры для защиты системы от возможных атак и использовать надежные методы обработки и валидации входных данных.

Полезные свойства инъекций

Инъекции обладают несколькими полезными свойствами:

1. Сохранение порядка: Если элементы двух множеств упорядочены и существует инъекция между ними, то порядок элементов сохраняется. То есть, если элементы в первом множестве идут в определенном порядке, то их образы во втором множестве также будут идти в том же порядке.
2. Обратимость: Инъекция может быть обратимой, то есть существует обратное отображение, которое каждому элементу изображения ставит в соответствие единственный элемент исходного множества. Это позволяет строить обратные инъекции и рассматривать инъекции как обратимые отображения.
3. Сохранение равенства: Если инъекция преобразует два различных элемента из первого множества в два различных элемента второго множества, то она сохраняет их различность. То есть, если элементы из первого множества не равны, то и их образы во втором множестве также не равны.

Эти свойства делают инъекции полезными инструментами в математике, позволяющими устанавливать соответствия между элементами различных множеств и анализировать их свойства.

Вопрос-ответ:

Что такое инъекция в математике?

Инъекция в математике — это отображение, которое каждому элементу из исходного множества сопоставляет уникальный элемент в целевом множестве. Другими словами, инъекция обладает свойством, что каждому элементу исходного множества соответствует только один элемент в целевом множестве.

Можете привести пример инъекции?

Да, конечно! Примером инъекции может служить отображение из множества натуральных чисел в себя, где каждому числу сопоставляется его удвоенное значение. Например, отображение f: N → N, где f(x) = 2x, является инъекцией, так как каждому числу x соответствует только одно число 2x.

Какие свойства обладает инъекция?

Инъекция обладает несколькими свойствами. Во-первых, каждому элементу исходного множества соответствует только один элемент в целевом множестве. Во-вторых, инъекция обратима, то есть каждому элементу в целевом множестве можно сопоставить только один элемент из исходного множества. Наконец, инъекция сохраняет порядок элементов, то есть если элементы a и b идут в порядке в исходном множестве, то их образы f(a) и f(b) также будут идти в порядке в целевом множестве.

Какую роль играет инъекция в математике?

Инъекция играет важную роль в математике, так как она позволяет установить однозначное соответствие между элементами двух множеств. Это может быть полезно, например, при доказательстве равномощности двух множеств или при построении функций с определенными свойствами. Инъекция также является одним из ключевых понятий в теории множеств и многих других разделах математики.