Что такое пропорция математика 6 класс

Пропорция – это математический термин, изучаемый в 6 классе. Пропорция включает в себя соотношение между четырьмя числами или выражениями. В статье вы найдете объяснение понятия пропорции, примеры решения задач и основные правила работы с этим математическим инструментом.

Пропорция – это математическое понятие, которое широко используется в различных областях нашей жизни. В математике пропорция является одним из основных понятий и позволяет нам сравнивать и устанавливать соотношения между различными величинами.

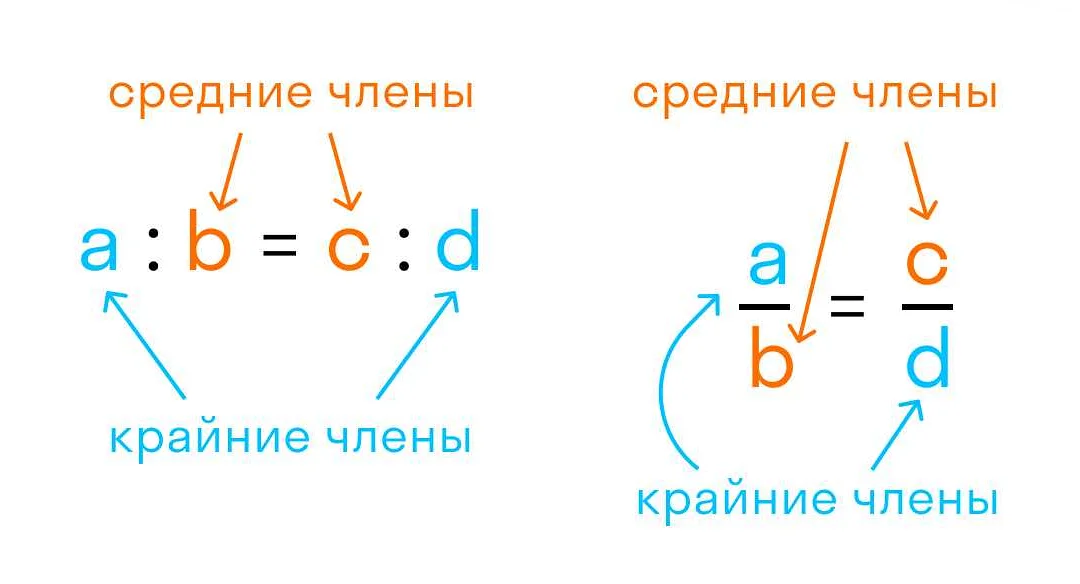
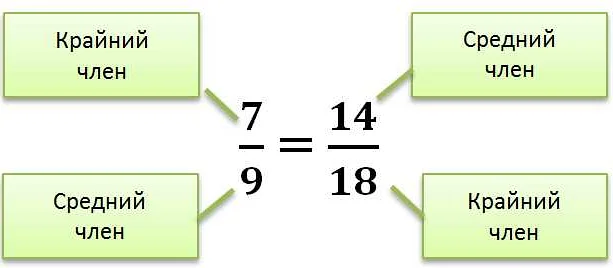
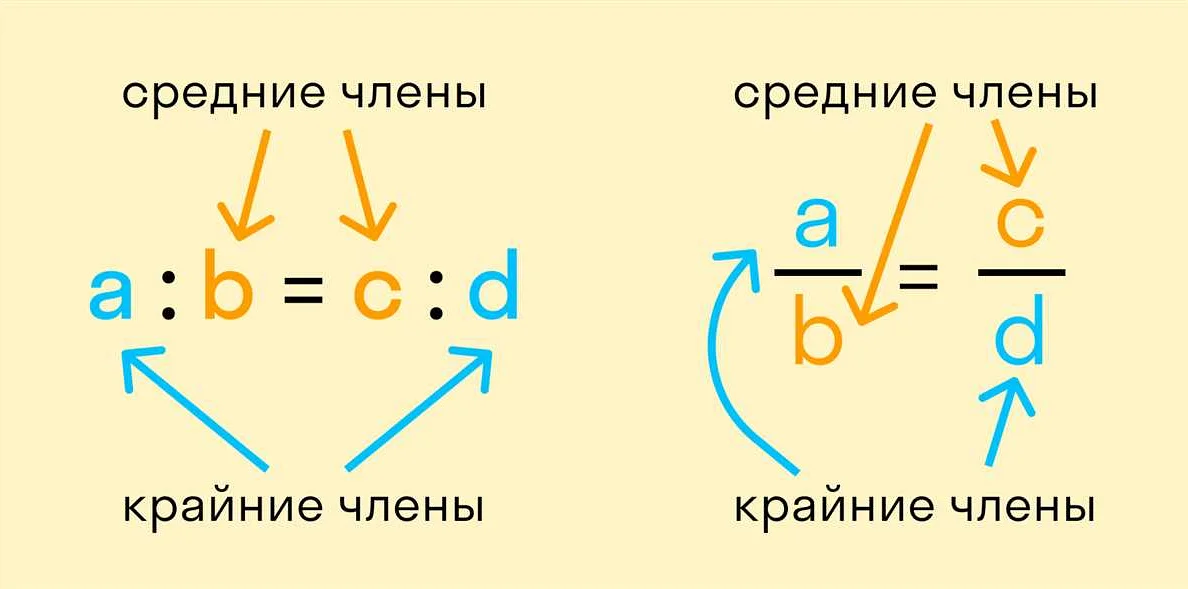
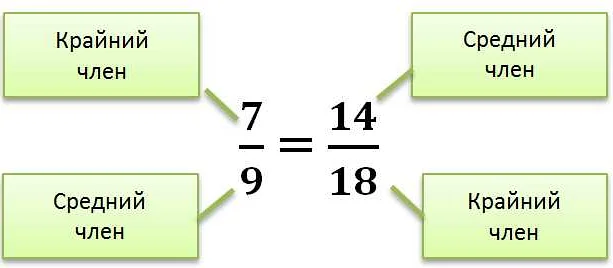
Пропорция состоит из четырех чисел или выражений, расположенных в две строки. Каждая строка пропорции называется прямым числом. Четыре числа, образующие пропорцию, могут быть представлены в виде a:b = c:d, где a, b, c и d – числа или выражения.

Важным свойством пропорции является то, что отношение между двумя числами в каждой строке пропорции всегда остается постоянным. Это означает, что отношение a:b всегда будет равно отношению c:d. Например, если у нас есть пропорция 2:4 = 5:10, то отношение 2:4 равно отношению 5:10, так как 2/4 = 5/10 = 1/2.

Пропорции играют важную роль в решении различных задач, связанных с пропорциональными отношениями величин. Они позволяют нам находить неизвестные значения и решать простые и сложные задачи в математике, экономике, физике и других областях. Понимание и умение работать с пропорциями является важным навыком для учащихся 6 класса и помогает им развивать логическое мышление и аналитические способности.

Определение пропорции

Пропорция выглядит следующим образом:

а:б = в:г

где а, б, в, г — это числа или величины, которые сравниваются.

Когда пропорция верна, мы можем сказать, что отношение между а и б равно отношению между в и г.

Пропорция может быть записана в разных формах. Например, а:б = в:г можно записать как:

а/б = в/г или а * г = б * в

В пропорции мы можем найти неизвестное значение, если известны все остальные. Для этого применяются правила пропорций и алгебраические операции.

Пропорции часто используются в различных задачах, где необходимо сравнить величины или найти неизвестное значение, основываясь на известных.

Видео по теме:

Простая пропорция и ее свойства

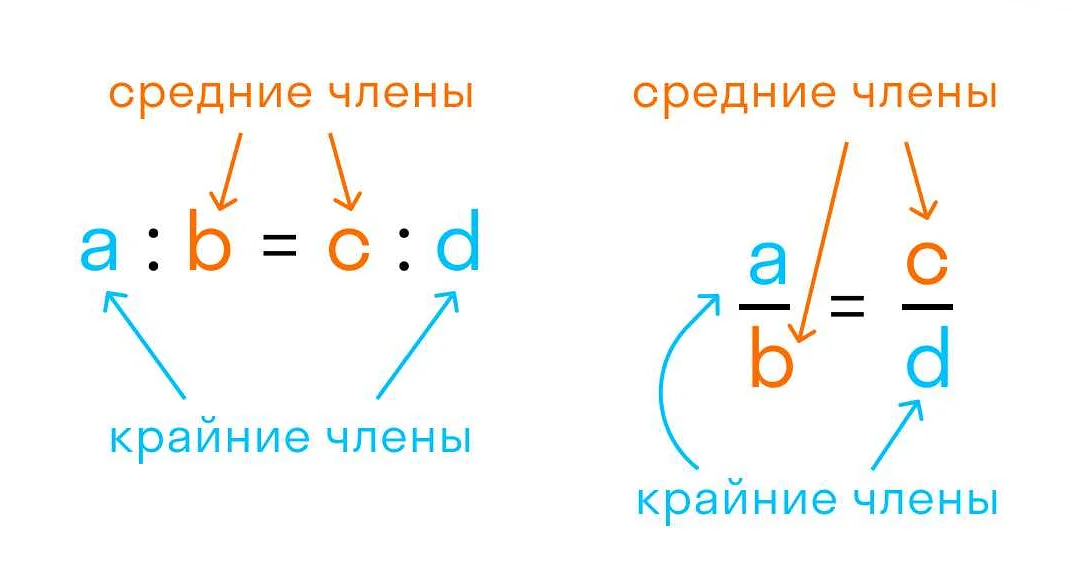
Свойства простой пропорции:

1. Если в пропорции а : b = c : d одна доля равна другой, то она равна их общему отношению: а : b = b : c = c : d.
2. Если в пропорции а : b = c : d одна доля равна сумме других двух долей, то пропорция называется пропорцией трех частей: a : b = b : (a + b).
3. Если в пропорции а : b = c : d одна доля равна произведению других двух долей, то пропорция называется пропорцией средних: a : b = (a + b) : (c + d).

Простая пропорция является важным инструментом в решении математических задач, особенно в геометрии и физике. Понимание ее свойств помогает упростить и ускорить процесс решения задач и делает математические вычисления более точными и надежными.

Как решать задачи на пропорцию

Решение задач на пропорцию требует следования нескольким шагам:

1. Прочитайте условие задачи внимательно и определите, какие величины известны, а какие нужно найти.
2. Составьте пропорцию, используя известные величины и неизвестную величину.
3. Разрешите пропорцию, чтобы найти значение неизвестной величины.
4. Проверьте ответ, применив его к условию задачи. Убедитесь, что он логически и численно верен.

При составлении пропорции, важно помнить о следующих правилах:

• Величины в пропорции должны быть однородными, то есть иметь одинаковую размерность.
• Величины в одной доле пропорции должны относиться к величинам в той же доле в пропорции.
• Порядок величин в пропорции не влияет на результат, поэтому вы можете менять местами числитель и знаменатель в долях.

После разрешения пропорции, если полученное значение неизвестной величины является разумным и соответствует условию задачи, то вы можете считать задачу решенной успешно.

Примеры решения задач на пропорцию

1. 1. Задача №1:

Автобус проехал 240 километров за 4 часа. Сколько времени понадобится автобусу, чтобы проехать 320 километров?

Решение:

Пусть x — искомое время.

Тогда можно составить пропорцию:

240 км / 4 ч = 320 км / x ч

Умножим обе части пропорции на x:

240 км * x / 4 ч = 320 км

Теперь найдем значение x:

x = 320 км * 4 ч / 240 км = 5 ч

Ответ: автобусу понадобится 5 часов, чтобы проехать 320 километров.

1. 1. Задача №2:

В магазине 15 метров ткани стоят 600 рублей. Сколько стоит 20 метров этой же ткани?

Решение:

Пусть x — искомая стоимость.

Тогда можно составить пропорцию:

15 м / 600 руб = 20 м / x руб

Умножим обе части пропорции на x:

15 м * x / 600 руб = 20 м

Теперь найдем значение x:

x = 20 м * 600 руб / 15 м = 800 руб

Ответ: 20 метров этой ткани стоят 800 рублей.

1. 1. Задача №3:

У курицы за 3 дня вылупилось 12 цыпленков. Сколько цыплят вылупится за 5 дней?

Решение:

Пусть x — искомое количество цыплят.

Тогда можно составить пропорцию:

12 цып / 3 дн = x цып / 5 дн

Умножим обе части пропорции на 5:

12 цып * 5 дн / 3 дн = x цып

Теперь найдем значение x:

x = 12 цып * 5 дн / 3 дн = 20 цыплят

Ответ: за 5 дней вылупится 20 цыплят.

Таким образом, решение задач на пропорцию требует умения составлять пропорции и находить неизвестные значения.

Прямая и обратная пропорциональность

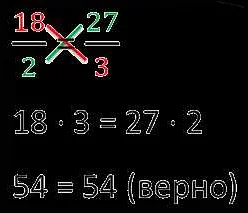
В математике существуют два вида пропорциональности: прямая и обратная.

Прямая пропорциональность – это связь между двумя величинами, при которой они изменяются в одном направлении. Если одна величина увеличивается, то и другая тоже увеличивается, и наоборот.

Например, если время, затраченное на прохождение трассы, прямо пропорционально скорости движения, то при увеличении скорости время уменьшается, а при уменьшении скорости время увеличивается. Математически это можно записать как:

Время = Коэффициент × Скорость

Обратная пропорциональность – это связь между двумя величинами, при которой они изменяются в противоположных направлениях. Если одна величина увеличивается, то другая уменьшается, и наоборот.

Например, если площадь поля обратно пропорциональна количеству времени, затраченного на его обработку, то при увеличении времени площадь поля уменьшается, а при уменьшении времени площадь поля увеличивается. Математически это можно записать как:

Площадь поля = Коэффициент ÷ Время

Прямая и обратная пропорциональность являются важными понятиями в математике и находят широкое применение в решении задач и расчетах.

Как определить пропорциональность

Для определения пропорциональности в математике необходимо проверить, выполняются ли два условия:

1. Значения величин должны быть неотрицательными.
2. Отношение между значениями величин должно быть постоянным.

Если оба условия выполнены, то можно сказать, что величины пропорциональны.

Например, рассмотрим пару величин: количество товара и его стоимость. Если при увеличении количества товара в два раза, его стоимость также увеличивается в два раза, то можно говорить о пропорциональности этих величин.

Обратите внимание, что пропорциональность может быть выражена с помощью различных математических операций, таких как умножение, деление, сложение или вычитание.

Применение пропорций в реальной жизни

Пропорции могут быть полезными при покупке товаров по фиксированной цене. Например, если одна коробка яблок стоит 100 рублей, а вторая коробка содержит в два раза больше яблок, то с помощью пропорции мы можем выяснить, сколько будет стоить вторая коробка. Если обозначить цену второй коробки как «х», то у нас будет пропорция: 100 (цена первой коробки) / 1 (количество яблок в первой коробке) = х (цена второй коробки) / 2 (количество яблок во второй коробке). Решив эту пропорцию, мы можем установить, что вторая коробка будет стоить 200 рублей.

Пропорции также могут быть полезными для расчета времени. Например, если известно, что для преодоления 100 километров требуется 2 часа, то с помощью пропорции мы можем выяснить, сколько времени потребуется для преодоления другого расстояния. Если обозначить время, требуемое для преодоления другого расстояния, как «х», то у нас будет пропорция: 2 (время для преодоления 100 километров) / 100 (расстояние) = х (время для преодоления другого расстояния) / другое расстояние. Решив эту пропорцию, мы можем установить, сколько времени потребуется для преодоления другого расстояния.

Пропорции также находят применение в строительстве. Например, при строительстве здания пропорции используются для создания архитектурных чертежей и планирования размеров различных частей здания.

Пропорции также применяются в финансовой сфере. Например, при расчете процента скидки на товар или расчете процентной ставки по кредиту пропорции могут быть полезными.

Применение пропорций в реальной жизни широко распространено и важно для решения различных задач в различных областях. Понимание и умение работать с пропорциями помогут нам применять математические знания в повседневной жизни.

Вопрос-ответ:

Что такое пропорция?

Пропорция — это равенство двух отношений. В математике пропорции используются для сравнения двух или более величин и нахождения неизвестных значений.

Как определить пропорцию?

Пропорция можно определить, если имеются четыре величины, и их отношения равны между собой. Пропорция обозначается символом «∝».

Как решать пропорцию?

Для решения пропорции нужно использовать правило трех членов. Если вам даны три из четырех величин, вы можете выразить неизвестное значение, умножив и делением других значений согласно пропорции.

Можете привести пример пропорции?

Конечно! Например, если 4 яблока стоят 80 рублей, то можно сказать, что цена одного яблока будет равна 20 рублям. В этом примере пропорция будет выглядеть так: 4/80 = 1/20.