Что такое r n в математике
Содержимое
- 1 Что такое r n в математике
- 1.1 Определение r n
- 1.2 Видео по теме:
- 1.3 Значение r n в математике
- 1.4 Примеры использования r n
- 1.5 Перевод r n на русский язык
- 1.6 Правила применения r n
- 1.7 Преимущества использования r n
- 1.8 Примеры задач с использованием r n
- 1.9 Вопрос-ответ:
- 1.9.0.1 Зачем использовать r n в математике?
- 1.9.0.2 Как правильно использовать r n в математике?
- 1.9.0.3 Какие еще символы можно использовать для создания новой строки в математике?
- 1.9.0.4 Какие есть примеры использования r n в математике?
- 1.9.0.5 Можно ли использовать r n в других областях, кроме математики?
- 1.9.0.6 Что такое r n в математике?
r n в математике обозначает множество вещественных чисел и является одной из основных концепций анализа. Узнайте, как оно связано с числами и применяется в различных областях математики.
В математике символ «r» обозначает число, которое представляет собой отношение двух величин или качеств, называемых числителем и знаменателем. Однако, что означает символ «n» в этом контексте? В математических выражениях «r n» означает возведение числа «r» в степень «n». Это означает, что число «r» будет умножаться само на себя «n» раз.
Например, если «r» равно 2 и «n» равно 3, то «r n» равно 2 в степени 3, что равно 2 * 2 * 2, или 8. Таким образом, «r n» показывает вычисление степени числа.
Использование «r n» может быть полезно при решении математических задач. Например, при расчете площади круга с радиусом «r», мы можем использовать формулу «Площадь = π r n», где «n» равно 2. Это позволяет нам вычислить площадь круга, умножив квадрат радиуса на число «π».
Также, «r n» может использоваться для вычисления корней числа. Например, если «r» равно 16 и «n» равно 4, то «r n» равно корню четвертой степени из 16, что равно 2. Это может быть полезно при решении задач, связанных с извлечением корней чисел.
Определение r n
Например, если r = 2 и n = 3, то rn будет равно 23 = 2 * 2 * 2 = 8.
Степень может быть любым целым числом, в том числе и отрицательным. В случае отрицательной степени, число rn равно обратному числу r, возведенному в положительную степень модуля n.
Например, если r = 3 и n = -2, то rn будет равно 3-2 = 1 / (3 * 3) = 1/9.
Определение rn имеет важное значение в математике и используется в различных областях, включая алгебру, геометрию и анализ.
Видео по теме:
Значение r n в математике

В выражении rn число r умножается на себя n раз. Например, если r = 2 и n = 3, то rn = 23 = 2 * 2 * 2 = 8.
Степени rn широко используются в различных областях математики, физики, экономики и других науках. Они помогают описывать процессы, моделировать явления и решать разнообразные задачи.
Например, степени часто используются при расчете процентов, при моделировании экономических тенденций, при описании роста популяции и многих других ситуациях.
В математике степени имеют свои особенности, такие как правила возведения в отрицательную степень, правила умножения степеней с одинаковыми основаниями и другие.
Использование степеней rn позволяет упростить выражения, решить сложные задачи и получить более точные результаты.
Поэтому знание и умение работать со степенями является важным навыком для всех, кто занимается математикой и ее приложениями.
Примеры использования r n

a = (a1, a2, a3)
Используя комбинацию r n, мы можем записать эту векторную нотацию в виде:
a = (a1, r n a2, r n a3)
Это позволяет нам четко разделить каждую компоненту вектора на новой строке для удобства чтения и записи.
Еще один пример использования комбинации r n — это запись системы уравнений. Рассмотрим систему уравнений:
a1x + b1y = c1
a2x + b2y = c2
Мы можем использовать комбинацию r n для записи этой системы уравнений в виде:
a1x + b1y = c1, r n a2x + b2y = c2
Это позволяет нам разделить каждое уравнение на новой строке, что делает запись системы уравнений более понятной и удобной для чтения.
Перевод r n на русский язык

Натуральные числа обычно обозначаются символом ℕ или иногда символом N. Это множество чисел, которые можно получить, начиная с 1 и последовательно увеличивая на единицу. Так, множество натуральных чисел можно представить как:
- ℕ = {1, 2, 3, 4, 5, …}
Использование символа r n в математике удобно для обозначения натуральных чисел, так как он является универсальным и принят во многих странах. Однако в русском языке его обычно переводят как «натуральные числа», чтобы избежать путаницы и непонимания.
Правила применения r n
В математике r n обозначает множество всех действительных чисел, то есть чисел, которые могут быть представлены десятичной дробью, как с конечным, так и с бесконечным количеством цифр после запятой. Данное множество включает в себя как рациональные числа (например, 1/2 или -3/4), так и иррациональные числа (например, корень из 2 или число Пи).
При использовании r n в математических выражениях следует учитывать следующие правила:
- В выражениях можно использовать основные арифметические операции: сложение (+), вычитание (-), умножение (*), деление (/) и возведение в степень (^).
- Можно использовать скобки для задания порядка выполнения операций.
- При использовании дробей рекомендуется сокращать их до несократимого вида.
- При работе с корнями следует учитывать, что в рациональном виде корень может быть представлен в виде десятичной дроби или в виде округленного значения.
- В некоторых случаях может быть необходимо округление значений, чтобы получить конечное число десятичных знаков.
- При использовании чисел с бесконечным количеством цифр после запятой следует учитывать особенности округления и приближения.
Применение данных правил позволяет корректно проводить математические операции с числами из множества r n и получать точные или приближенные значения в зависимости от ситуации.
Преимущества использования r n
1. Удобство записи: операция r n позволяет компактно и наглядно записывать степени чисел. Например, запись 23 означает возведение числа 2 в куб, что экономит пространство и упрощает понимание.
2. Математические вычисления: использование операции r n позволяет легко выполнять различные математические операции, такие как умножение, деление и извлечение корня. Например, для вычисления квадратного корня из числа можно использовать запись 250.5.
3. Описание зависимости: операция r n позволяет описывать зависимость одного значения от другого. Например, если у нас есть формула A = B2, то это означает, что значение A зависит от квадрата значения B.
4. Применение в различных областях: операция r n широко используется не только в математике, но и в других науках и инженерии. Она позволяет описывать законы природы, физические процессы, экономические модели и т.д.
Таким образом, использование операции r n в математике имеет множество преимуществ, включая удобство записи, легкость вычислений, описание зависимости и применение в различных областях знания.
Примеры задач с использованием r n
Рассмотрим несколько примеров задач, в которых используется понятие r n.
Пример 1:
Пусть дано множество точек на плоскости. Найти такую прямую, которая проходит через наибольшее количество точек.
Для решения этой задачи можно воспользоваться понятием r n. Пусть у нас имеется n точек. Тогда мы можем провести прямую через две любые точки, то есть количество возможных прямых будет равно C(n, 2) = n(n-1)/2. Но не все эти прямые будут проходить через большое количество точек. Найдем такую прямую, что количество точек, лежащих на ней, будет максимальным. Для этого рассмотрим все возможные прямые и найдем такую, на которой лежит наибольшее количество точек. Эта прямая и будет искомой.
Пример 2:
Пусть дано множество отрезков на плоскости. Найти такую прямую, которая пересекает наибольшее количество отрезков.
Данная задача сводится к задаче нахождения медианы множества отрезков при помощи понятия r n. Пусть у нас имеется n отрезков. Тогда количество возможных прямых будет равно n. Найдем такую прямую, которая пересекает наибольшее количество отрезков. Для этого рассмотрим все возможные прямые и найдем такую, которая пересекает наибольшее количество отрезков. Эта прямая и будет искомой.
Таким образом, понятие r n находит применение в решении различных задач, связанных с геометрией и комбинаторикой.
Вопрос-ответ:
Зачем использовать r n в математике?
R n в математике используется для обозначения новой строки. Оно позволяет сделать текст более читабельным и удобным для анализа. Кроме того, r n может быть полезно при работе с файлами, особенно в случаях, когда необходимо сохранить форматирование текста.
Как правильно использовать r n в математике?
Чтобы использовать r n в математике, вам нужно просто добавить его в нужное место в тексте. Например, если вы хотите создать новую строку после определенной формулы или выражения, то можете вставить r n после него. В результате получится более читабельный текст.
Какие еще символы можно использовать для создания новой строки в математике?
Помимо r n, также можно использовать символы такие как n, t, f или v для создания новой строки в математике. Однако, r n является наиболее распространенным и рекомендуемым символом для этой цели.
Какие есть примеры использования r n в математике?
Примеры использования r n в математике включают в себя добавление новой строки перед или после выражения, формулы или уравнения. Например, если вы пишете математическое решение в текстовом формате, то можете использовать r n для разделения каждого шага решения.
Можно ли использовать r n в других областях, кроме математики?
Да, r n можно использовать не только в математике, но и во многих других областях, где требуется создание новой строки. Например, в программировании или при работе с текстовыми файлами. R n позволяет сделать текст более структурированным и удобным для чтения.
Что такое r n в математике?
В математике обозначение r n часто используется для обозначения натуральных чисел, то есть положительных целых чисел. Также r n может обозначать множество натуральных чисел.

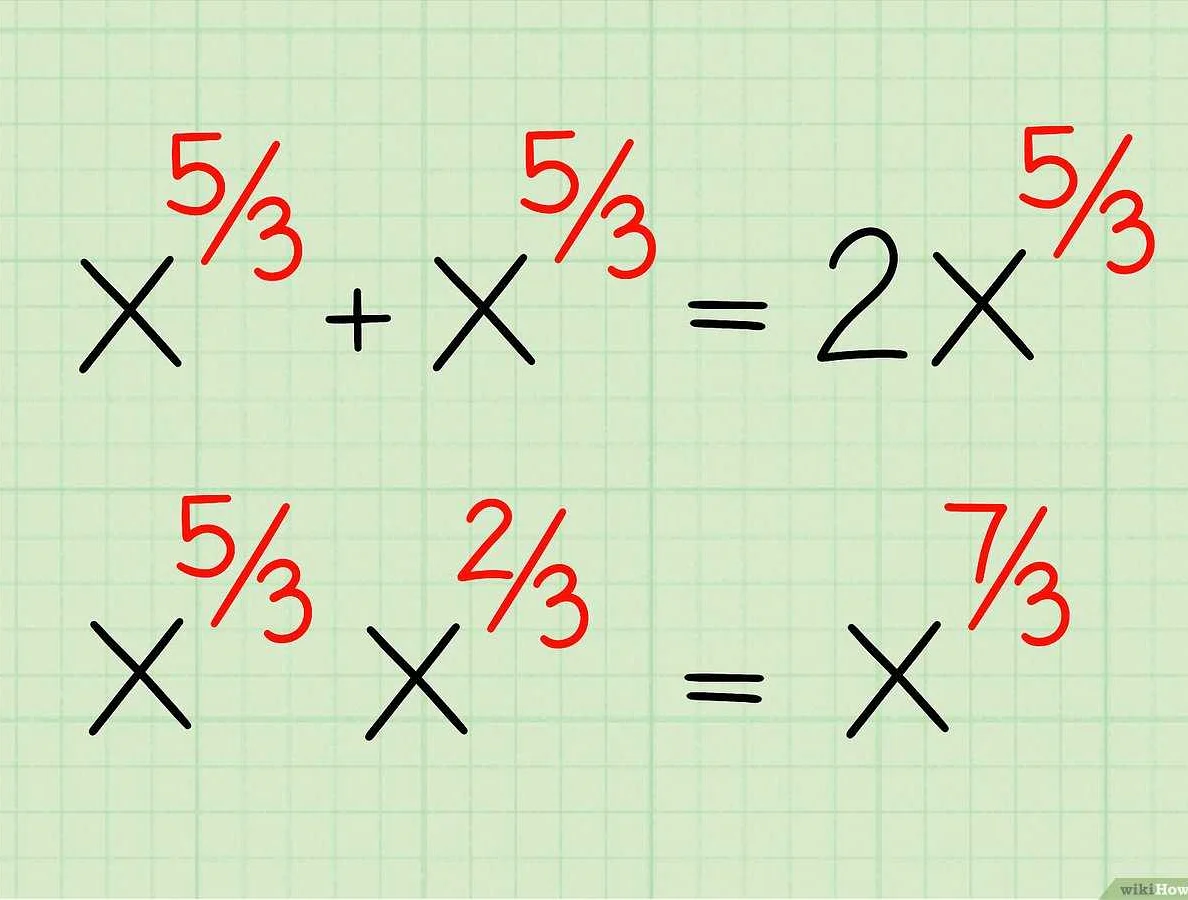


Спасибо за статью! Она действительно помогла мне разобраться, что такое r n в математике. Я всегда задавалась вопросом, зачем это нужно, и теперь все стало понятно. Такое обозначение оказывается очень полезным, особенно когда нужно указать диапазон значений или последовательность чисел. Примеры использования, которые вы привели, помогли мне лучше усвоить материал. Теперь я уверена, что смогу правильно записать и понять математические формулы. Очень благодарна за информативную и понятную статью!
Я всегда задаюсь вопросами о математике и всегда рада, когда нахожу ответы. Недавно я услышала о таком понятии, как «r n» в математике, и решила узнать, что это такое. Оказывается, «r n» означает множество всех действительных чисел, то есть чисел, которые можно представить на числовой оси. Это очень интересно, потому что это означает, что «r n» включает в себя не только целые числа, но и десятичные дроби и иррациональные числа, такие как корень из двух или пи. Конечно, этим множеством можно пользоваться во многих математических задачах. Например, если мы решаем уравнение и ищем его корни, мы будем искать решения в «r n». Для меня это новое и увлекательное понятие в математике, и я с нетерпением жду, чтобы узнать еще больше и использовать его в своих учебных заданиях.
Чудесно, наконец-то я поняла, что такое r n в математике! Это оказалось не так сложно, как я думала. R n обозначает множество всех рациональных чисел в пределах от 0 до 1. Это значит, что в этом диапазоне есть бесконечно много чисел, которые можно записать в виде обыкновенной дроби. Например, такие числа, как 1/2, 1/3, 2/5 и так далее. R n позволяет нам классифицировать эти числа и изучать их свойства. Например, мы можем узнать, какие дроби являются простыми, а какие составными, или какие из них можно представить в виде бесконечной десятичной дроби. Более того, r n позволяет нам проводить различные математические операции с этими числами, такие как сложение, вычитание, умножение и деление. Вот такая интересная находка! Теперь я понимаю, что такое r n и как его использовать в математике.
Очень интересная статья! Я всегда задавалась вопросом о том, что означает r n в математике. Ваше объяснение было исчерпывающим и понятным. Теперь я точно знаю, что r n обозначает множество всех рациональных чисел. Примеры использования, которые вы привели, помогли мне лучше понять, как применять эту концепцию в практике. Теперь я смогу использовать r n для описания множества всех дробей или чисел вида a/b, где a и b — целые числа, а b не равно нулю. Спасибо за полезную информацию! Теперь я чувствую себя увереннее в понимании математических понятий. Буду ждать новых интересных статей на вашем сайте!