Что такое степень числа в математике 5 класс определение
Содержимое
Степень числа в математике 5 класс – это понятие, которое описывает, сколько раз число нужно умножить на себя. Узнайте определение и примеры степеней чисел для пятиклассников.
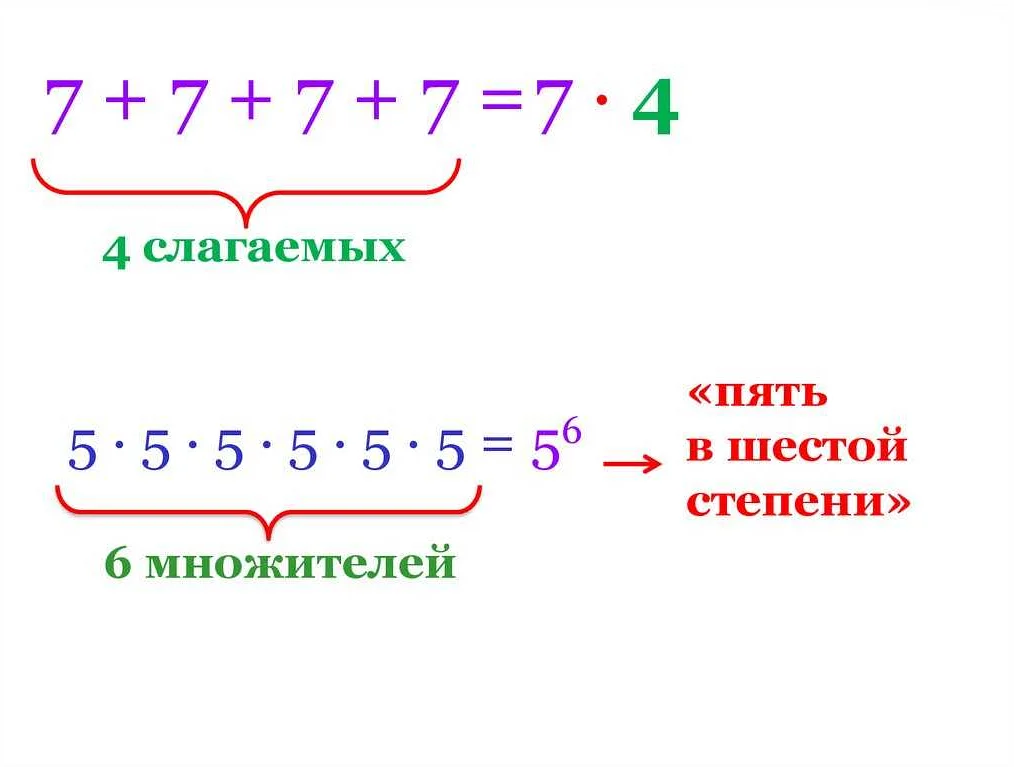
Степень числа – это математическая операция, которая позволяет возвести число в натуральную степень. В математике степень числа обозначается символом «^». Например, число 2 возводится в степень 3 записывается как 2^3.
В степени числа указывается два числа: основание и показатель степени. Основание – это число, которое возведено в степень. Показатель степени – это число, которое указывает, сколько раз нужно умножить основание на само себя.
Например, 2^3 означает, что число 2 нужно умножить на само себя три раза: 2^3 = 2 × 2 × 2 = 8.
Степень числа может быть любым натуральным числом. Если показатель степени равен 0, то результатом всегда будет 1. Например, 2^0 = 1. Если показатель степени равен 1, то результатом будет само число. Например, 2^1 = 2.
Определение степени числа

Число, которое умножается, называется основанием, а количество раз, на которое оно умножается, называется показателем степени. Результатом операции является степень числа.
Степень числа обозначается в виде основания, затем знака возведения в степень и показателя степени.
Например, степень числа 2 в виде записи выглядит так: 23. Здесь число 2 является основанием, а число 3 — показателем степени. Результатом вычисления этой степени будет число 8, так как 2 * 2 * 2 = 8.
Важно понимать, что возведение в степень — это повторное умножение числа на само себя, количество раз равное показателю степени. Таким образом, степень числа позволяет удобным образом записывать многократные умножения и сокращать запись.
Степень числа может быть как положительной, так и отрицательной. В случае отрицательной степени, число знаменатель и становится обратным к основанию. Например, 2-3 = 1 / (2 * 2 * 2) = 1 / 8.
Также степень числа может быть равна 0. В этом случае результатом будет 1. Например, 20 = 1.
Операция возведения в степень является важной и широко используется в математике и науке для решения различных задач и формулировки законов и принципов.
В таблице ниже приведены примеры возведения чисел в степень:
ОснованиеПоказатель степениСтепень
| 2 | 3 | 8 |
| 3 | 2 | 9 |
| 5 | 4 | 625 |
Основные понятия
Степень числа обозначается с помощью знака «в степени». Например, число 2 в кубе обозначается как 23. Здесь число 2 является основанием степени, а число 3 — показателем степени.
Основные понятия, связанные со степенями чисел:
ТерминОписаниеПример
| Основание степени | Число, которое умножается на себя | В степени 2: 32, основание — 3 |
| Показатель степени | Количество раз, которое основание умножается на себя | В степени 2: 32, показатель — 2 |
| Степень числа | Результат операции умножения числа на себя определенное количество раз | 32 = 3 * 3 = 9 |
Степени чисел широко используются в различных областях математики и физики, а также в реальной жизни, например, в финансовых расчетах или при изучении процентов.
Примеры степени числа
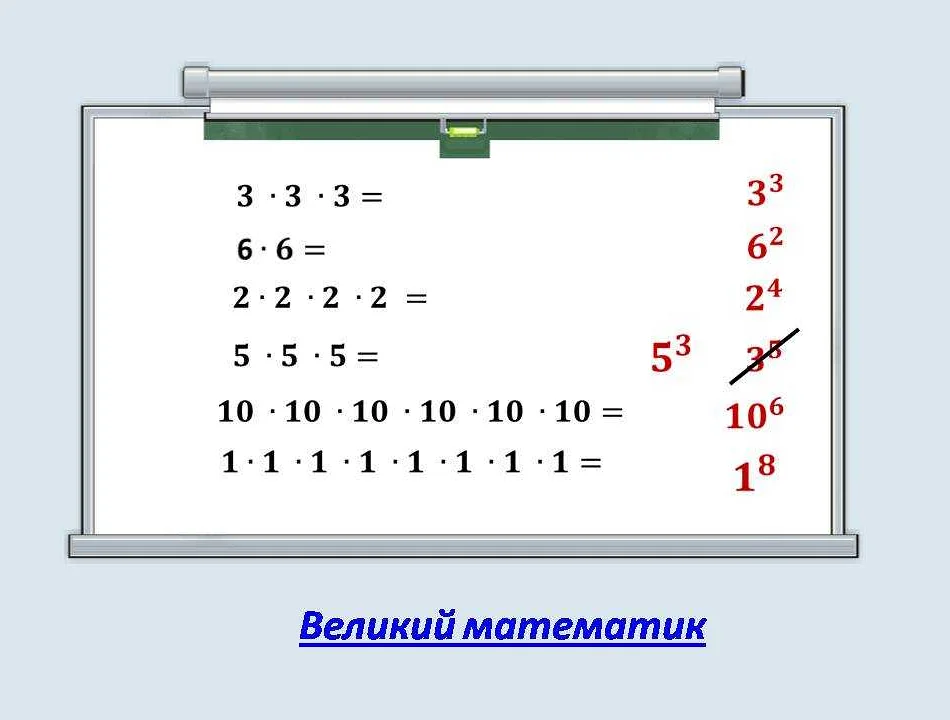
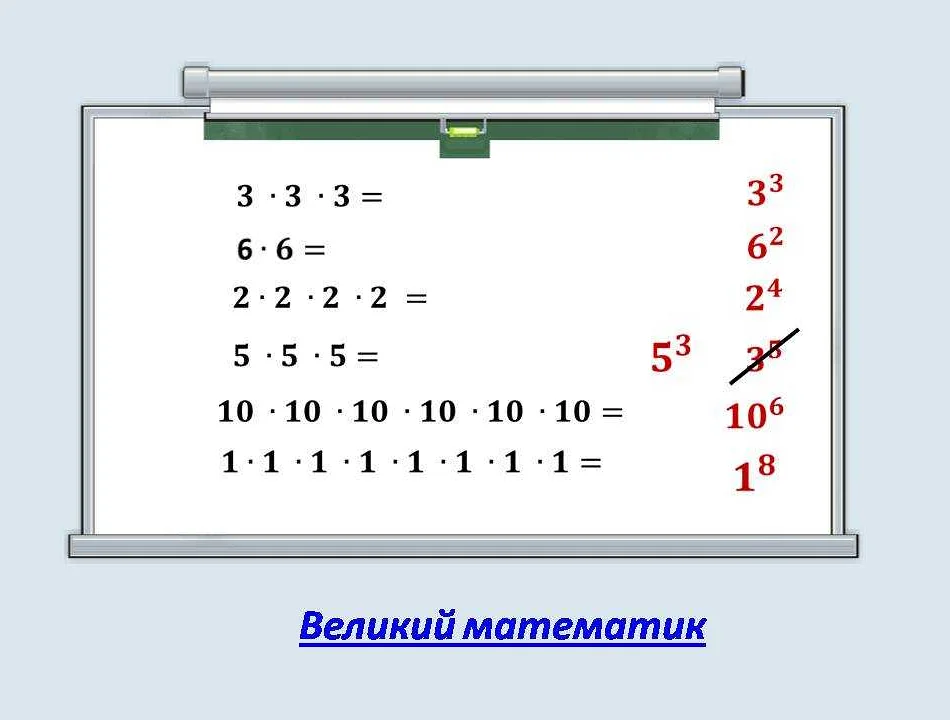
Например, если число 2 возвести в степень 3, это означает, что нужно умножить число 2 на само себя 3 раза:
- 2 в степени 3 = 2 x 2 x 2 = 8
Также можно возвести число в отрицательную степень. В этом случае число будет располагаться в знаменателе дроби:
- 2 в степени -2 = 1/2 x 1/2 = 1/4
Если число возвести в степень 0, то результат будет равен 1:
- 2 в степени 0 = 1
Таким образом, степень числа позволяет упрощать выражения и производить различные вычисления.
Степень числа больше 1
Например, если у нас есть число 2 в степени 3, это означает, что мы должны умножить число 2 само на себя три раза:
СтепеньЧисло в степениРезультат
| 1 | 2 | 2 |
| 2 | 2 * 2 | 4 |
| 3 | 2 * 2 * 2 | 8 |
Таким образом, число 2 в степени 3 равно 8.
Степень числа больше 1 может быть записана с помощью знака «^». Например, 2^3 означает число 2 в степени 3.
Степень числа больше 1 позволяет удобно записывать и вычислять числа, которые нужно умножить само на себя несколько раз. Это особенно полезно при работе с большими числами или при выполнении сложных математических операций.
Степень числа меньше 1

Например, если число 2 возведено в степень -1, то получится следующее выражение: 2-1. Результатом этого выражения будет 1/2, так как при возводении в отрицательную степень число инвертируется и знаменатель становится числителем.
Также, степень числа меньше 1 может быть представлена в виде десятичной дроби. Например, число 5 возведенное в степень -2 будет равно 1/25, что равно 0.04 в десятичной форме.
Степень числа меньше 1 используется для решения различных задач и уравнений, а также для изучения процентов и долей.
Важно понимать, что степень числа меньше 1 может быть как положительной, так и отрицательной, и результатом всегда будет десятичная дробь.
Свойства степени числа
У степени числа есть несколько свойств, которые помогают упростить вычисления и работу с числами:
- Свойство умножения: при умножении чисел в степени, степень получившегося числа равна сумме степеней исходных чисел. Например, (2^3) * (2^4) = 2^(3+4) = 2^7.
- Свойство деления: при делении чисел в степени, степень получившегося числа равна разности степеней исходных чисел. Например, (4^5) / (4^3) = 4^(5-3) = 4^2.
- Свойство возведения в степень: при возведении числа в степень, степень получившегося числа равна произведению степени основания и степени, в которую возводят число. Например, (3^2)^4 = 3^(2*4) = 3^8.
- Свойство степени нуля: любое число, кроме нуля, в степени нуль равно единице. Например, 5^0 = 1.
- Свойство степени единицы: любое число, возведенное в степень единицы, равно самому числу. Например, 7^1 = 7.
Эти свойства позволяют упростить вычисления со степенями и делают работу с числами более удобной.
Вопрос-ответ:
Что такое степень числа?
Степень числа — это операция, при которой число умножается само на себя несколько раз.
Как определить степень числа?
Для определения степени числа нужно умножить это число само на себя нужное количество раз. Например, 2 в степени 3 означает, что число 2 нужно умножить на себя 3 раза (2 * 2 * 2 = 8).
Какие есть примеры степени чисел в математике?
Некоторые примеры степеней чисел: 2 в степени 3 равно 8, 5 в степени 2 равно 25, 10 в степени 0 равно 1 и т.д.
Как вычислить отрицательную степень числа?
Для вычисления отрицательной степени числа нужно взять обратное значение числа и возвести его в положительную степень. Например, (-2) в степени -3 равно (-1/2) в степени 3, что равно -1/8.
Применение степени числа в реальной жизни

Одним из примеров применения степени числа в реальной жизни является экономика. Когда мы рассматриваем проценты, мы фактически используем степень числа. Например, если вы вкладываете деньги под процентную ставку, то каждый год ваше начальное вложение будет умножаться на (1 + процентная ставка)^n, где n — количество лет.
Еще одним примером является физика. В законе Ньютона о гравитации степень числа используется для вычисления силы притяжения между двумя телами. Формула имеет вид F = G * (m1 * m2) / r^2, где F — сила притяжения, G — гравитационная постоянная, m1 и m2 — массы тел, r — расстояние между ними.
Еще одним примером применения степени числа является компьютерная графика. В трехмерной графике координаты точки x, y и z часто преобразуются с помощью степени числа для создания эффекта перспективы и удаленности.
Таким образом, степень числа имеет множество применений в реальной жизни, начиная от экономики и заканчивая компьютерной графикой. Понимание этой математической операции помогает нам решать различные задачи и применять ее в различных областях нашей жизни.

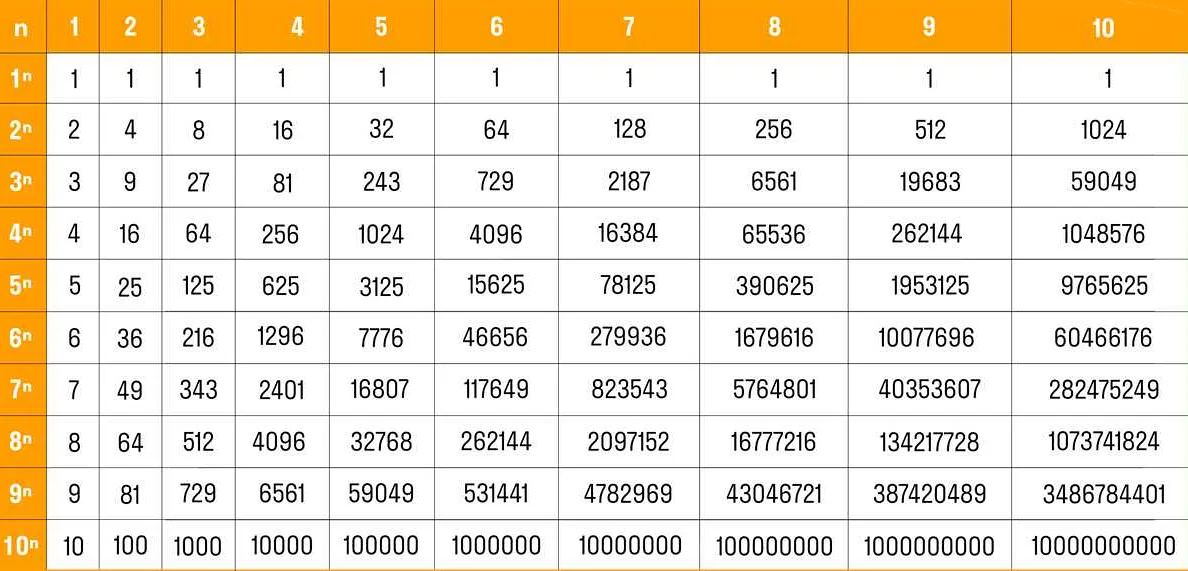
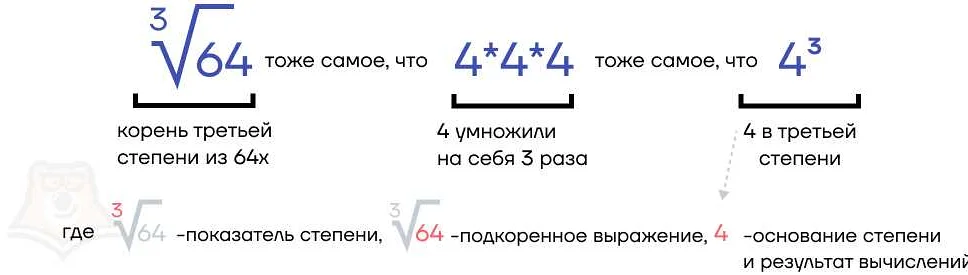
Степень числа в математике — это особое понятие, которое помогает нам упростить большие числа и сделать их более компактными. Когда число возведено в степень, оно умножается само на себя определенное количество раз. Например, 2 в степени 3 будет равно 2 * 2 * 2 = 8. Это очень удобно, когда нам нужно записать число, которое повторяется много раз. Например, 10 в шестой степени будет равно 10 000 000. Вот какая мощь в степенях чисел! Также важно знать, что степень может быть как положительной, так и отрицательной. Если степень отрицательная, то число будет находиться в знаменателе дроби. Например, 4 в степени -2 будет равно 1/4 * 1/4 = 1/16. Надеюсь, что объяснение было понятным и помогло вам разобраться с понятием степени числа. Удачи в изучении математики!