Что такое радиус 3 класс математика

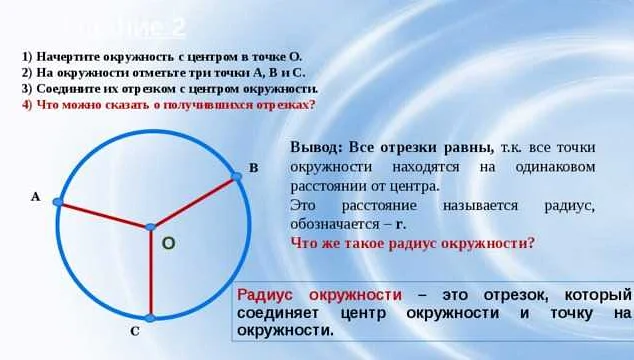
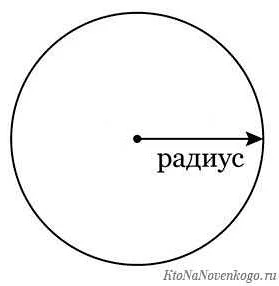
Радиус – это отрезок, соединяющий центр окружности с любой ее точкой. В математике радиус 3 класса используется для изучения основных свойств окружностей, определения и измерения радиуса, а также для решения задач по построению и применению окружностей в реальной жизни.

Радиус — одно из ключевых понятий в математике, которое изучается уже в третьем классе. Он широко используется в геометрии и алгебре, а также находит применение в других науках и технических областях. В этой статье мы рассмотрим, что такое радиус и как его можно измерить.

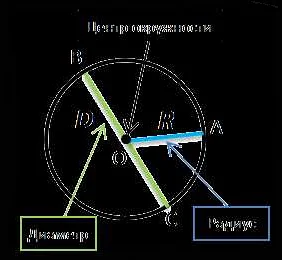
Радиусом называется отрезок, соединяющий центр окружности и любую точку на ее границе. Он является половиной диаметра и обозначается символом r. Знание радиуса очень важно для определения площади и длины окружности, а также для решения задач по построению геометрических фигур.

Например, представим себе окружность радиусом 5 сантиметров. Это значит, что любой отрезок, проведенный от центра этой окружности до ее границы, будет иметь длину 5 сантиметров. Зная радиус, мы можем вычислить площадь этой окружности, используя формулу S = πr², где π — математическая константа, примерное значение которой равно 3,14.

Таким образом, понимание радиуса и его свойств позволяет нам проводить точные измерения и решать задачи, связанные с геометрией и алгеброй. Учебная программа по математике в третьем классе предусматривает изучение этого понятия и его применение в различных задачах. Знание радиуса поможет детям улучшить свои навыки в решении математических задач и лучше понять мир, окружающий нас.

Определение радиуса в математике

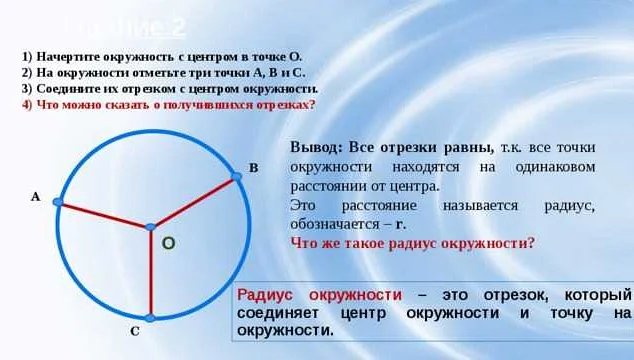
В математике радиус широко используется для решения различных задач. Например, радиус может использоваться для вычисления площади круга или объема шара. Для этого нужно знать значение радиуса и использовать соответствующую формулу.

Примеры использования радиуса в математике:

Пример	Задача	Решение
Пример 1	Найти площадь круга с радиусом 5 см.	Формула площади круга: S = π * r^2 S = 3.14 * 5^2 = 3.14 * 25 = 78.5 см^2
Пример 2	Найти объем шара с радиусом 2 м.	Формула объема шара: V = (4/3) * π * r^3 V = (4/3) * 3.14 * 2^3 = (4/3) * 3.14 * 8 = 33.52 м^3

Таким образом, радиус — это важное понятие в математике, которое помогает решать различные задачи, связанные с окружностями и шарами.

Видео по теме:

Радиус в геометрии

В геометрии радиус обозначается символом r или R. Он является положительным числом, так как длина отрезка не может быть отрицательной или равной нулю.

Радиус позволяет определить другие важные параметры окружности, такие как диаметр, площадь и длина окружности. Диаметр окружности равен удвоенному радиусу, площадь окружности рассчитывается по формуле П = πr2, где π (пи) — математическая постоянная, приближенное значение которой равно 3,14159.

Радиус также применяется при решении различных задач, связанных с окружностями и шарами. Например, для определения площади кругового сегмента или объема шара необходимо знать его радиус.

В геометрии радиус имеет множество применений и широко используется при анализе и изучении различных фигур и объектов.

Примеры радиуса в окружности

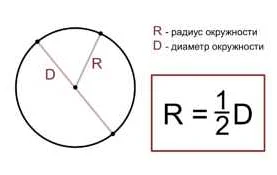
Примеры радиуса в окружности:

1. Пусть длина радиуса «r» равна 5 см. Тогда длина окружности будет равна 2πr = 2π * 5 см = 10π см.
2. Если радиус «r» равен 8 м, то площадь окружности будет равна πr² = π * 8² м² = 64π м².
3. Если радиус «r» равен 10 м, то длина дуги окружности будет равна πr = π * 10 м ≈ 31,42 м.

Таким образом, радиус в окружности может использоваться для решения различных задач, связанных с окружностями, таких как вычисление длины окружности, площади окружности и длины дуги окружности.

Вопрос-ответ:

Что такое радиус в математике?

В математике радиус — это отрезок, соединяющий центр окружности с любой ее точкой. Он является одной из основных характеристик окружности и определяет ее размер.

Как найти радиус окружности?

Чтобы найти радиус окружности, нужно знать либо длину окружности и применить формулу r = C / (2π), где r — радиус, C — длина окружности, π — математическая константа, равная примерно 3.14159, либо знать площадь окружности и применить формулу r = √(S / π), где r — радиус, S — площадь окружности, π — математическая константа.

Какие примеры можно привести для радиуса в 3 классе?

В 3 классе примеры для радиуса могут быть связаны с рисованием и измерением окружностей. Например, можно попросить учеников нарисовать окружность с заданным радиусом, измерить радиус уже нарисованной окружности с помощью линейки или длинной нити, или решить задачу на нахождение радиуса, если известна длина окружности или площадь окружности.

Можно ли провести 2 окружности с одинаковым радиусом?

Да, можно провести две окружности с одинаковым радиусом. Радиус влияет только на размер окружности, но не на ее положение в пространстве. Поэтому можно провести сколько угодно окружностей с одинаковым радиусом в разных местах.

Можно ли изменить радиус окружности?

Да, радиус окружности можно изменить. Если изменить длину отрезка, соединяющего центр окружности с любой ее точкой, то изменится и радиус. Однако, чтобы окружность осталась окружностью, радиус нужно изменять пропорционально, то есть увеличивать или уменьшать его в одно и то же количество раз.

Что такое радиус в математике?

В математике радиус — это отрезок, соединяющий центр окружности с любой точкой на ней. Он является одной из основных характеристик окружности.

Как найти радиус окружности, если известна площадь?

Чтобы найти радиус окружности, если известна площадь, нужно воспользоваться формулой радиуса окружности: r = √(S/π), где S — площадь окружности, а π — число Пи (примерно равно 3,14).

Радиус в круге: формула и примеры

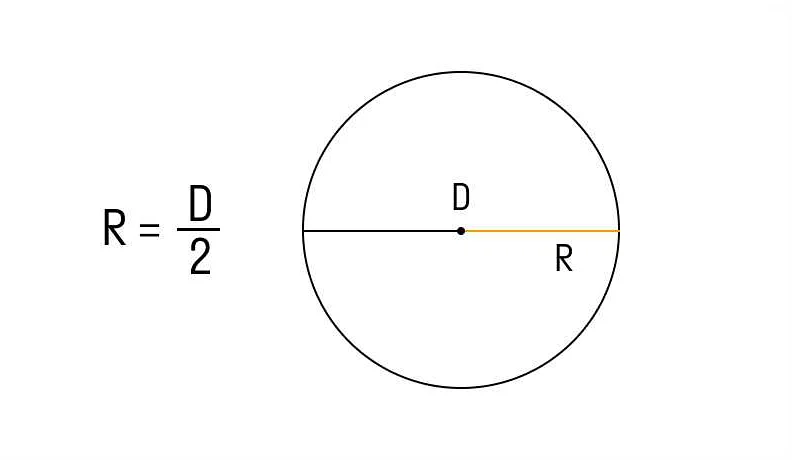
Формула для вычисления радиуса круга:

r = d/2

где r — радиус круга, а d — диаметр круга.

Примеры:

1. Допустим, у нас есть круг с диаметром 10 см. Чтобы найти радиус, нужно разделить диаметр на 2: r = 10/2 = 5. Радиус круга равен 5 см.

2. Если у нас есть круг с диаметром 8 м, то радиус равен половине диаметра: r = 8/2 = 4. Радиус круга равен 4 м.

Таким образом, радиус в круге можно вычислить, разделив диаметр на 2, согласно формуле r = d/2.

Радиус в теореме Пифагора: примеры и решение

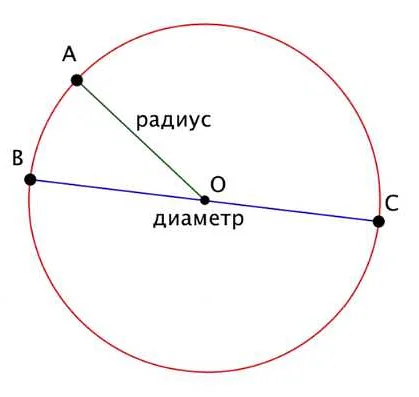
Теорема Пифагора устанавливает связь между длинами сторон прямоугольного треугольника. Согласно этой теореме, квадрат длины гипотенузы равен сумме квадратов длин катетов.

Допустим, у нас есть прямоугольный треугольник ABC, где стороны AC и BC — катеты, а сторона AB — гипотенуза. Если длины катетов равны 3 и 4, то какую длину имеет гипотенуза?

Для решения данной задачи применим теорему Пифагора:

AB2 = AC2 + BC2

Подставим известные значения:

AB2 = 32 + 42

AB2 = 9 + 16

AB2 = 25

Для того чтобы найти длину гипотенузы, возьмем квадратный корень из полученного значения:

AB = √25

AB = 5

Таким образом, длина гипотенузы треугольника ABC равна 5.

Радиус в треугольнике: определение и свойства

Свойства радиуса в треугольнике:

1. Радиус в треугольнике равен половине высоты, проведенной к противоположной стороне.
2. Радиус в треугольнике является медианой, которая делит сторону треугольника на две равные части.
3. Радиус в треугольнике является биссектрисой угла, и делит его на два равных угла.
4. Радиус в треугольнике является ортомедианой, которая проходит через вершину треугольника и перпендикулярна к противоположной стороне.

Радиус в треугольнике играет важную роль в геометрии, так как позволяет определить различные свойства и характеристики треугольника. Он также используется при решении задач на нахождение площади и периметра треугольника.

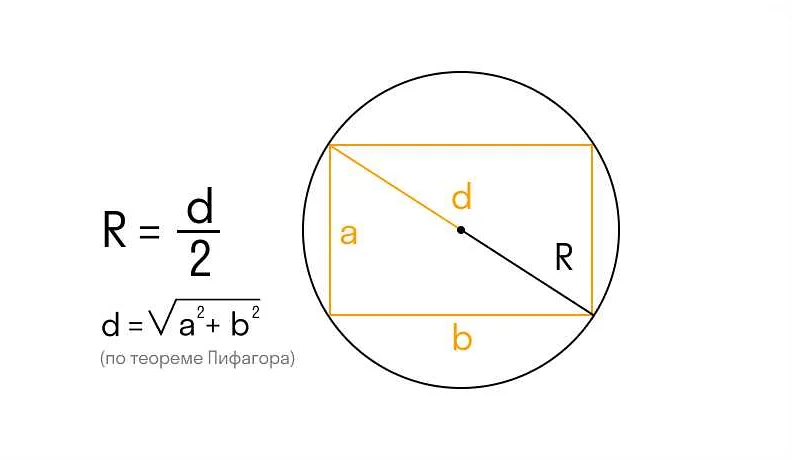
Радиус в прямоугольнике: определение и формула

Формула для вычисления радиуса в прямоугольнике следующая:

Радиус = √((длина^2 + ширина^2)/4)

где:

• длина — длина прямоугольника;
• ширина — ширина прямоугольника.

Например, если длина прямоугольника равна 8 единицам, а его ширина — 6 единицам, то радиус можно вычислить следующим образом:

Радиус = √((8^2 + 6^2)/4) = √((64 + 36)/4) = √(100/4) = √25 = 5

Таким образом, радиус прямоугольника с длиной 8 и шириной 6 равен 5 единицам.

Радиус в квадрате: определение и свойства

Для нахождения радиуса в квадрате необходимо умножить радиус окружности на самого себя.

Формула для нахождения радиуса в квадрате: R^2 = R * R, где R — радиус окружности.

Свойства радиуса в квадрате:

СвойствоОписание

Величина	Радиус в квадрате является положительным числом.
Единицы измерения	Единицы измерения радиуса в квадрате зависят от единиц измерения радиуса окружности.
Связь с площадью	Площадь окружности можно выразить с помощью радиуса в квадрате и числа pi (π): S = π * R^2.