Что такое радиус в математике

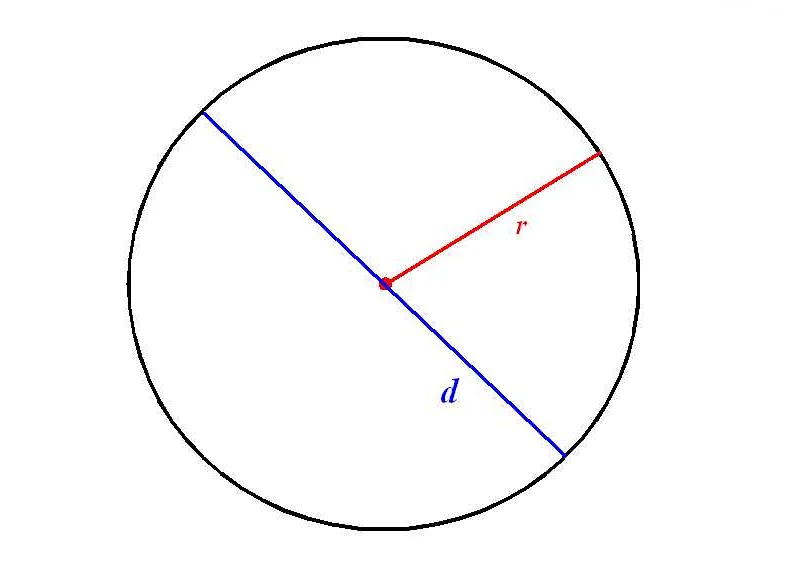
Радиус в математике – это расстояние от центра окружности или сферы до ее края. Он является одним из основных параметров, определяющих геометрические свойства этих фигур. Узнайте, как измеряется радиус и как он влияет на размер и форму окружности или сферы.

Радиус – это одно из фундаментальных понятий в математике, которое является ключевым элементом в решении многих задач и проблем. Определение радиуса необходимо знать всем, кто хочет разбираться в геометрии и алгебре. В математике радиус используется для определения центра окружности или сферы, а также для измерения расстояния от центра до любой точки на окружности или сфере.

Радиус обозначается символом «r» и является отрезком, соединяющим центр окружности или сферы с любой точкой на их поверхности. Он играет важную роль в геометрии, так как определяет множество свойств и характеристик фигуры, к которой он относится. Например, радиус окружности позволяет вычислить ее длину, площадь и дугу, а радиус сферы определяет ее объем и площадь поверхности.

Примеры использования радиуса можно найти не только в геометрии, но и в других областях математики. Например, в тригонометрии радиус используется для нахождения углов, в алгебре – для определения графиков функций, а в физике – для решения задач о движении и силе.

Знание определения и свойств радиуса позволяет более глубоко понять мир вокруг нас и применять математические методы в различных сферах нашей жизни. Поэтому освоение этого понятия является важной задачей для всех, кто интересуется математикой и стремится к познанию нового.

Радиус в математике: определение и примеры

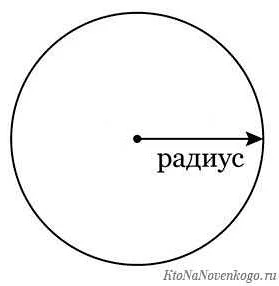
В геометрии радиус представляет собой отрезок, соединяющий центр окружности или сферы с ее любой точкой. Радиус является постоянным для данной окружности или сферы, то есть все отрезки, соединяющие центр с точками окружности или сферы, имеют одинаковую длину.

Радиус также используется для определения различных характеристик окружности или сферы. Например, чтобы найти площадь окружности, нужно умножить квадрат радиуса на число Пи (π). Формула для вычисления площади окружности выглядит следующим образом: S = π * r^2.

В тригонометрии радиус используется для определения тригонометрических функций на окружности. На единичной окружности радиус равен 1, и точки на окружности могут быть представлены в виде пары координат (x, y), где x и y — это значения синуса и косинуса соответственно.

Примеры использования радиуса:

1. Нахождение площади окружности: S = π * r^2.
2. Вычисление длины окружности: L = 2 * π * r.
3. Определение тригонометрических функций на окружности.

Таким образом, радиус является важным понятием в математике и используется для определения различных характеристик окружности или сферы, а также в тригонометрии для нахождения тригонометрических функций на окружности.

Что такое радиус в геометрии

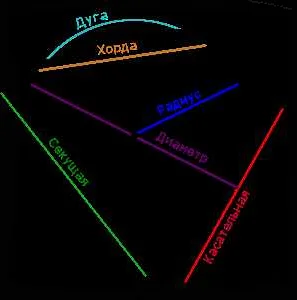
Радиус окружности обозначается символом r и является постоянным для данной окружности. Длина радиуса может быть выражена через длину окружности или площадь круга по формулам:

Длина радиуса: r = C / (2π)

Площадь круга: S = πr^2

Знание радиуса позволяет решать разнообразные задачи, например, находить площадь и длину окружности, определять расстояние от точки до центра окружности и многое другое.

Радиус также используется в геометрии при решении задач на нахождение площади и объема сферы.

Определение радиуса в теории множеств

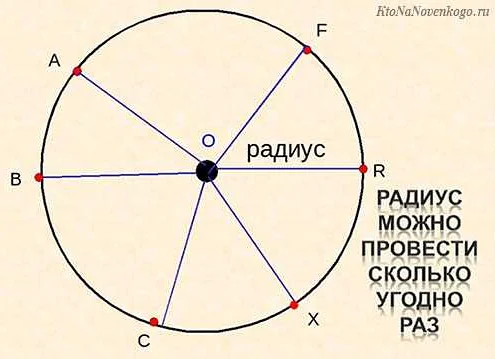
В основном, радиус используется для определения размера или длины объекта, такого как окружность или сфера. Если рассматривать окружность, то радиусом будет являться расстояние от центра окружности до любой ее точки. В случае сферы, радиусом будет являться расстояние от центра сферы до ее поверхности.

Радиус может быть положительным или нулевым числом. Если радиус равен нулю, то это означает, что центр объекта совпадает с его поверхностью или границей.

Важно отметить, что в теории множеств радиус может быть определен и для других геометрических фигур, таких как эллипс, прямоугольник и многоугольник. В каждом случае формула расчета будет отличаться, но основная идея остается прежней – радиус определяет расстояние от центра фигуры до ее границы или поверхности.

Пример:

Рассмотрим пример с окружностью. Пусть у нас есть окружность с радиусом 5 см. Это означает, что для любой точки на окружности расстояние от центра окружности до этой точки составляет 5 см.

Таким образом, радиус в теории множеств является важной концепцией для определения размера и расстояния в различных геометрических фигурах.

Радиус в тригонометрии: понятие и свойства

В тригонометрии радиус может быть использован для определения основных тригонометрических функций, таких как синус, косинус и тангенс. Например, синус угла (sin) определяется как отношение противолежащего катета к гипотенузе прямоугольного треугольника. Гипотенуза в данном случае равна радиусу, а противолежащий катет — расстоянию от центра круга до конечной точки на его окружности, которая соответствует данному углу.

Свойства радиуса в тригонометрии также могут быть использованы для нахождения площади круга. Площадь круга равна произведению квадрата радиуса на число Пи (π). Также радиус может быть использован для вычисления длины окружности по формуле: длина окружности = 2πr, где р — радиус.

Радиус в тригонометрии имеет множество других свойств и применений. Он может быть использован для нахождения высоты и площади треугольника, а также для решения различных задач геометрии и физики.

Радиус в математическом анализе: основные понятия

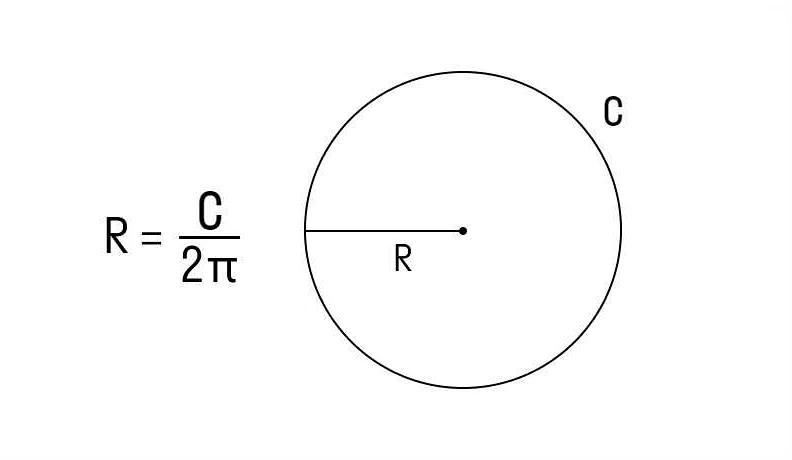
Радиус можно представить как меру удаленности от некоторой точки или объекта. В контексте математического анализа он широко используется для определения окрестностей точек и сходимости функций и последовательностей.

Одним из наиболее распространенных применений радиуса в математическом анализе является определение радиуса сходимости степенного ряда. Радиус сходимости показывает, в какой области вокруг центра ряда разложения функция будет сходиться абсолютно и условно.

Кроме того, радиус также используется для определения окрестности точки функции. Окрестность — это интервал, который содержит все точки, находящиеся на определенном расстоянии от центральной точки. Радиус окрестности задает это расстояние и позволяет определить, насколько близко расположены точки в окрестности к центральной точке.

Таким образом, радиус в математическом анализе является важным понятием, которое помогает определить свойства функций и последовательностей. Он используется для определения сходимости рядов и окрестностей точек, и его значение определяет диапазон точек, которые находятся на определенном расстоянии от центральной точки.

Значение радиуса в круговых функциях

В круговых функциях радиус обычно обозначается символом r. Значение радиуса определяет длину отрезка, соединяющего начало координат (обычно точку (0, 0)) и точку на окружности, которая соответствует заданному углу.

Например, если угол равен 0 радиан, то точка на окружности, соответствующая этому углу, совпадает с началом координат, и длина радиуса равна 0.

Если угол равен π/2 радиан, то точка на окружности, соответствующая этому углу, находится на расстоянии радиуса от начала координат.

Таким образом, значение радиуса в круговых функциях определяет удаленность точки на окружности от начала координат и позволяет вычислять различные характеристики и свойства, связанные с этой точкой.

Угол (в радианах)Значение радиуса

0	0
π/4	r/√2
π/2	r
3π/4	r/√2
π	0

В таблице приведены значения радиуса для некоторых углов в радианах. Они позволяют наглядно представить, как меняется радиус в круговых функциях в зависимости от значения угла.

Примеры использования радиуса в геометрии

ПримерОписание

1	Вычисление площади круга
2	Определение длины окружности
3	Нахождение расстояния между двумя точками на плоскости
4	Нахождение координат центра окружности
5	Построение вписанной окружности в треугольник

В каждом из этих примеров радиус играет важную роль и позволяет решить задачу с точностью и эффективностью. Знание свойств и формул, связанных с радиусом, позволяет геометрам проводить различные вычисления и построения в пространстве и на плоскости.

Применение радиуса в физике и инженерии

В физике радиус используется для определения геометрических характеристик объектов. Например, в механике радиус может определять длину вектора, отображающего положение объекта в пространстве. Также радиус может быть использован для вычисления площади поверхности или объема тела.

В инженерии радиус находит широкое применение при проектировании и изготовлении различных изделий. Например, радиус используется при создании криволинейных поверхностей на деталях или при определении радиуса изгиба трубопроводов и кабелей. Также радиус может быть использован для определения радиуса деталей и инструментов.

Применение радиуса в физике и инженерии позволяет учитывать геометрические особенности объектов и создавать оптимальные конструкции с заданными параметрами. Корректное определение радиуса позволяет точнее описывать и анализировать системы, что в конечном итоге способствует повышению эффективности и надежности различных процессов.

Вопрос-ответ:

Что такое радиус в математике?

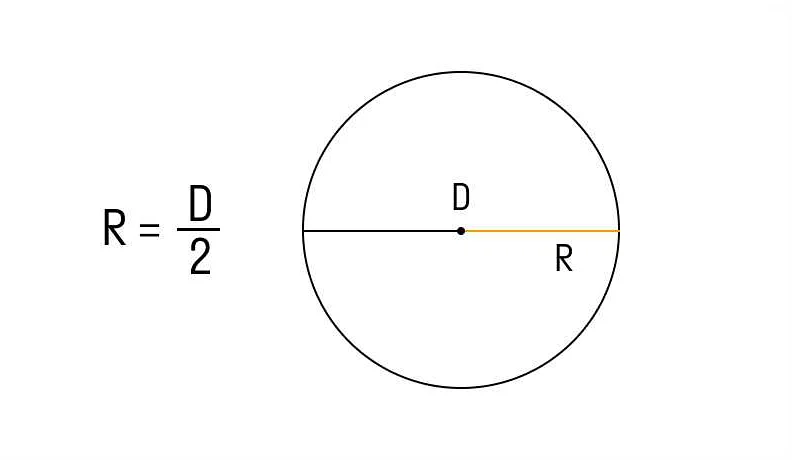
Радиус — это отрезок, соединяющий центр окружности с ее любой точкой. Он является половиной диаметра окружности и определяет ее размер.

Как найти радиус окружности?

Для нахождения радиуса окружности нужно разделить диаметр на 2. Формула для вычисления радиуса: R = D/2, где R — радиус, D — диаметр.

Как радиус связан с площадью окружности?

Радиус и площадь окружности связаны формулой: S = π * R^2, где S — площадь, R — радиус, π (пи) — математическая константа, приближенное значение которой равно 3,14.

Как радиус влияет на периметр окружности?

Радиус окружности влияет на ее периметр по формуле: P = 2 * π * R, где P — периметр окружности, R — радиус, π (пи) — математическая константа, приближенное значение которой равно 3,14.

Значение радиуса в компьютерной графике и программировании

В компьютерной графике и программировании понятие радиуса также играет важную роль. Радиус может использоваться для определения размеров геометрических фигур, создания анимации, управления движением объектов и многих других задач.

В графических программных библиотеках, таких как OpenGL или Canvas, радиус используется для определения размера окружности или круга. Например, при создании окна или отображении графических объектов, радиус задается в пикселях и определяет, насколько далеко от центра объекта должны быть видимые точки.

В алгоритмах компьютерного зрения, таких как распознавание образов или определение границ объектов, радиус может использоваться для определения размера области интереса. Например, при распознавании лица радиус может определить, какие пиксели следует анализировать для определения наличия лица на изображении.

В игровой разработке радиус может использоваться для определения зон взаимодействия объектов. Например, при определении столкновений между объектами игры радиус может определить, насколько близко должны находиться объекты друг к другу для срабатывания столкновения.

Таким образом, радиус в компьютерной графике и программировании является важным параметром, который определяет размеры и взаимодействия объектов, а также используется для решения различных задач в области компьютерного зрения и игровой разработки.

Видео по теме: