Что такое равнобедренный треугольник 4 класс математика
Содержимое
- 1 Что такое равнобедренный треугольник 4 класс математика
- 1.1 Определение равнобедренного треугольника
- 1.2 Основные понятия равнобедренного треугольника
- 1.3 Свойства и характеристики равнобедренного треугольника
- 1.4 Расчеты и формулы для равнобедренного треугольника
- 1.5 Примеры задач с равнобедренными треугольниками
- 1.6 Решение задач на построение равнобедренного треугольника
- 1.7 Интересные факты о равнобедренных треугольниках
- 1.8 Вопрос-ответ:
- 1.9 Задачи для самостоятельного решения
- 1.10 Видео по теме:
Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Учебная статья по математике для 4 класса, где дается определение равнобедренного треугольника и приводятся примеры его построения и свойств.
Равнобедренный треугольник – это особый вид треугольника, у которого две стороны равны между собой. Он назван так из-за того, что у него две равные стороны, которые называются боковыми сторонами. В равнобедренном треугольнике также два угла при основании равны между собой.
Равнобедренные треугольники можно увидеть в разных предметах окружающего мира. Например, крыша дома может иметь форму равнобедренного треугольника. Также равнобедренные треугольники используются в архитектуре, в строительстве мостов, в геометрических узорах на коврах и тканях.
В математике равнобедренные треугольники играют важную роль. Они помогают нам решать задачи и находить неизвестные значения, используя свойства этого особого вида треугольника.
Если в задаче дан равнобедренный треугольник, мы можем использовать его свойства, чтобы находить различные значения. Например, зная длину одной стороны и угол при основании, мы можем найти длину другой стороны с помощью теоремы синусов. Также, зная длину боковой стороны и угол при основании, мы можем найти длину основания треугольника.
Изучение равнобедренных треугольников помогает развивать навыки логического мышления и абстрактного мышления у учащихся. Они учатся применять математические знания на практике и решать задачи с помощью геометрических фигур.
Определение равнобедренного треугольника
Для того чтобы найти равнобедренный треугольник, необходимо проверить условие равенства длин сторон и равности соответствующих углов. Если две стороны треугольника равны между собой и два соответствующих угла равны, то треугольник является равнобедренным.
Равнобедренные треугольники имеют множество свойств и особенностей. Например, высота, проведенная из вершины угла при основании, делит основание на две равные части. Также, медиана, проведенная из вершины угла при основании, делит треугольник на две равные половины.
Знание и понимание равнобедренных треугольников позволяет решать различные математические задачи и находить различные свойства и особенности треугольников.
Основные понятия равнобедренного треугольника
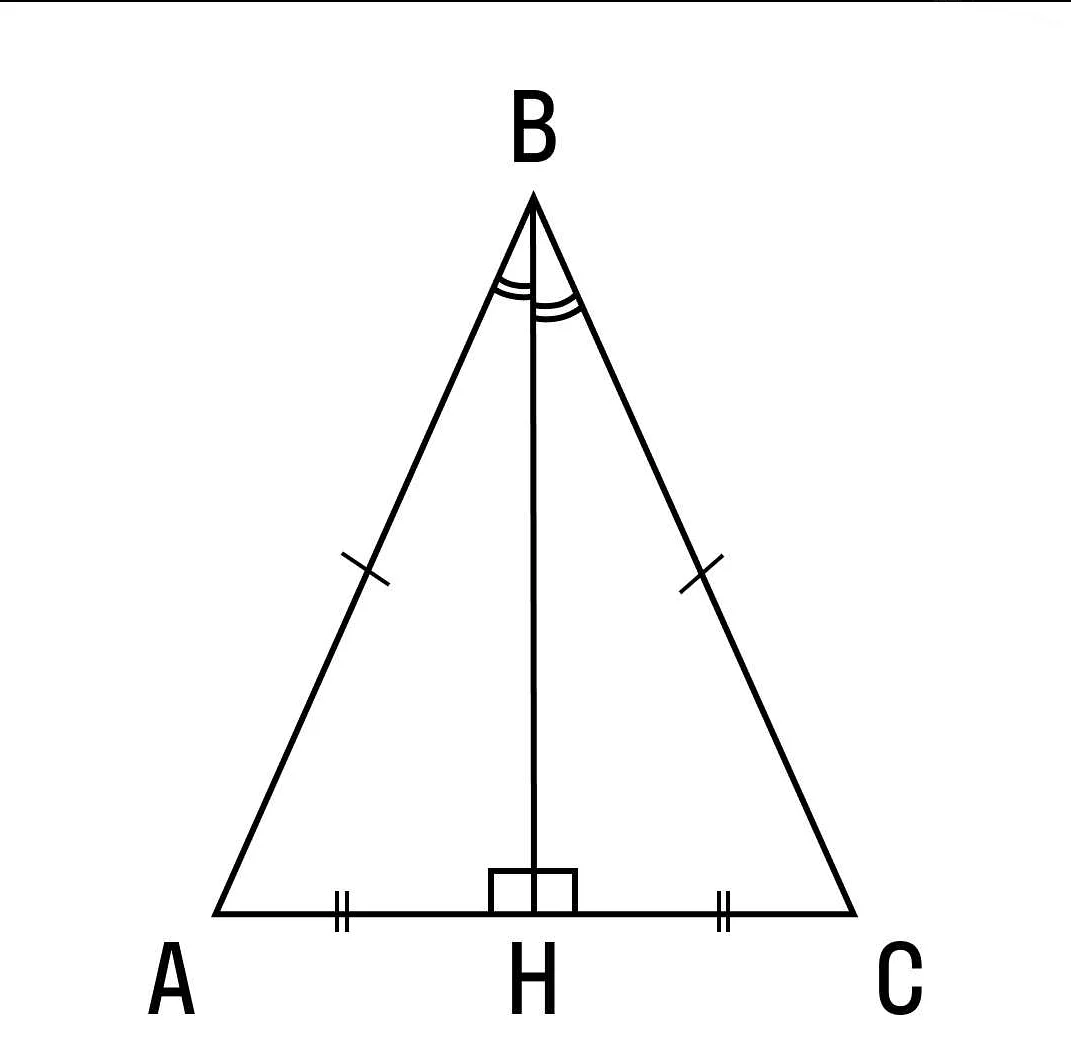
В равнобедренном треугольнике основание может быть либо больше, либо меньше боковых сторон. Если основание больше боковых сторон, то такой треугольник называется остроугольным равнобедренным треугольником. Если основание меньше боковых сторон, то такой треугольник называется тупоугольным равнобедренным треугольником.
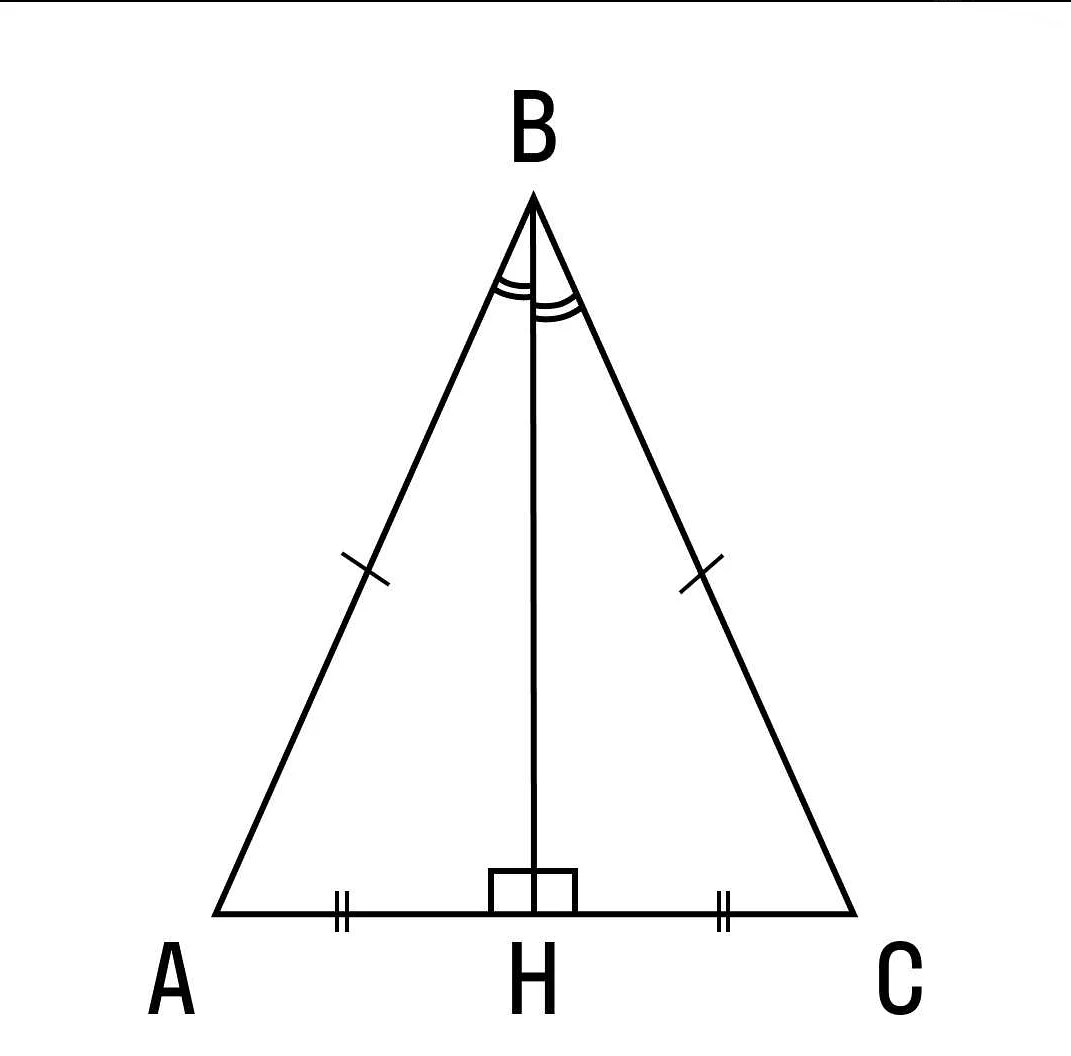
У равнобедренного треугольника также есть высота. Высота равнобедренного треугольника — это перпендикуляр, опущенный из вершины треугольника на основание. Все высоты равнобедренного треугольника равны между собой и делят треугольник на два равных прямоугольных треугольника.
Свойства и характеристики равнобедренного треугольника
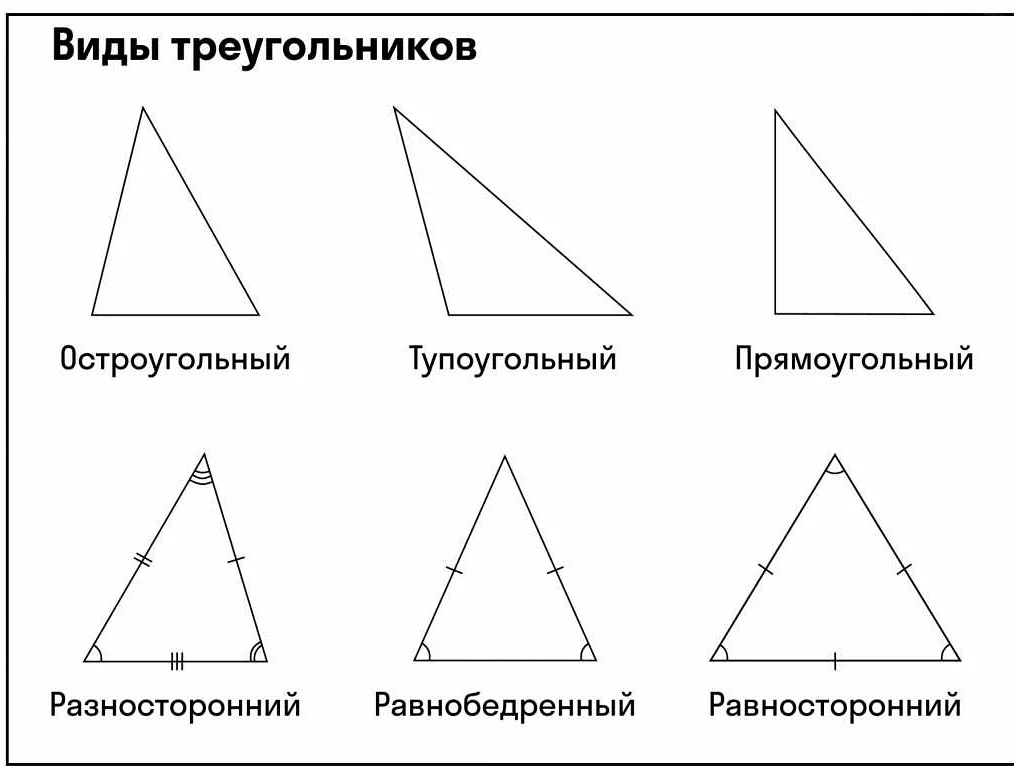
Свойства равнобедренного треугольника:
- У равнобедренного треугольника две равные боковые стороны.
- Углы при основании равны между собой.
- Угол, образованный боковой стороной и основанием, называется углом при основании. В равнобедренном треугольнике углы при основании равны между собой.
- Перпендикуляр, опущенный из вершины треугольника на основание, делит его на два равных отрезка.
- Высота, опущенная из вершины на основание, является биссектрисой угла при основании.
Например:
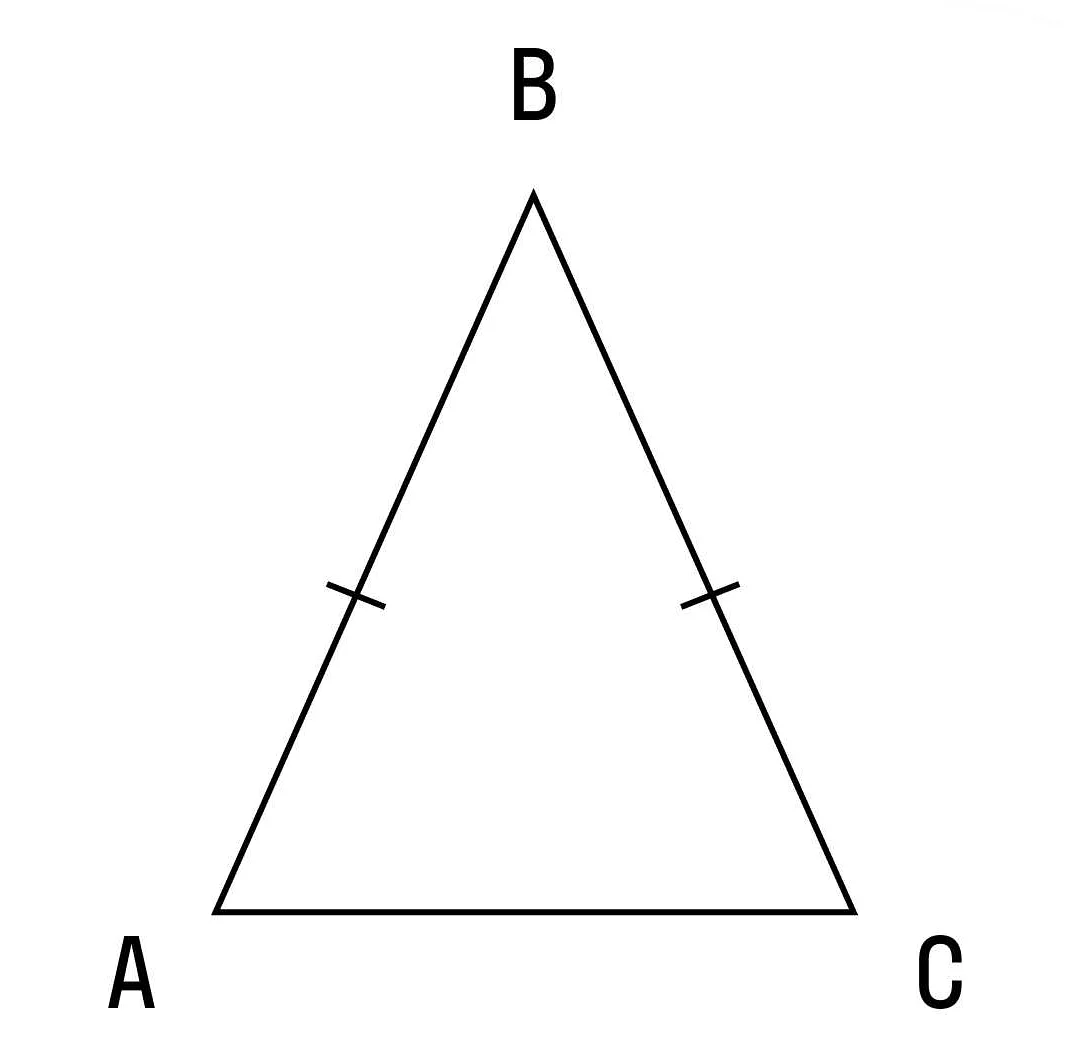
В треугольнике ABC сторона AB равна стороне AC. Также угол BAC равен углу BCA. Такой треугольник называется равнобедренным треугольником.
Расчеты и формулы для равнобедренного треугольника
1. Периметр равнобедренного треугольника – это сумма длин всех его сторон. Чтобы найти периметр, нужно сложить длины всех трех сторон. Если две стороны равны, то формула для периметра будет выглядеть так: P = 2a + b, где P – периметр треугольника, a – длина равных сторон, b – длина третьей стороны.
2. Площадь равнобедренного треугольника можно найти, используя формулу: S = (b * h) / 2, где S – площадь треугольника, b – длина третьей стороны, h – высота треугольника, которая проходит из вершины до основания.
3. Высоту равнобедренного треугольника можно найти, используя формулу: h = √(a2 — (b/2)2), где h – высота треугольника, a – длина равных сторон, b – длина третьей стороны.
4. Угол между равными сторонами равнобедренного треугольника можно найти, используя формулу: α = (180° — β) / 2, где α – угол между равными сторонами, β – угол между третьей стороной и одной из равных сторон.
Используя эти формулы и расчеты, можно проводить различные математические операции с равнобедренными треугольниками и находить нужные значения.
Примеры задач с равнобедренными треугольниками
Пример 1:
В равнобедренном треугольнике один из углов является прямым. Определите, какие углы различны и найдите их величину.
Решение:
Поскольку угол является прямым, его величина равна 90 градусов. Другие два угла равны между собой и их сумма составляет 90 градусов. Значит, каждый из них равен 45 градусам.
Пример 2:
Найдите периметр равнобедренного треугольника, если известны длины основания и боковой стороны.
Решение:
Периметр равнобедренного треугольника можно найти, сложив длины всех его сторон. Если основание равно a, а боковая сторона равна b, то периметр равен a + b + b. Таким образом, периметр равнобедренного треугольника равен 2b + a.
Пример 3:
Дан равнобедренный треугольник с высотой h. Найдите площадь треугольника, если известны длины основания и высоты.
Решение:
Площадь равнобедренного треугольника можно найти, умножив длину основания на высоту и разделив полученное значение на 2. Таким образом, площадь равнобедренного треугольника равна (a * h) / 2.
Пример 4:
Дан равнобедренный треугольник с углом в 60 градусов. Найдите величину остальных двух углов.
Решение:
Поскольку угол в равнобедренном треугольнике делится пополам, остальные два угла будут равны между собой и каждый из них будет составлять (180 — 60) / 2 = 60 градусов.
Решение задач на построение равнобедренного треугольника
Чтобы построить равнобедренный треугольник, необходимо выполнить следующие шаги:
- Нарисовать отрезок AB, который будет основанием треугольника.
- Взять циркуль и установить одну из его ножек в точку A.
- Сделать разметку на отрезке AB, используя вторую ножку циркуля. На отрезке должны оказаться две точки C и D.
- Провести линии AC и AD, которые будут боковыми сторонами треугольника.
- Убедиться, что сторона BC равна стороне BD. Если это не так, то нужно сделать новую разметку на отрезке AB.
Теперь у нас есть равнобедренный треугольник ABC (или ABD), в котором сторона AB является основанием, а стороны AC и AD являются боковыми.
При решении задач на построение равнобедренного треугольника обязательно следует учитывать условия задачи. Например, если в задаче указано, что треугольник должен быть равнобедренный и равносторонний, то все стороны треугольника должны быть равны между собой.
Решение задач на построение равнобедренного треугольника может быть применено для решения различных практических задач, например, в строительстве или геодезии. Понимание основных принципов построения равнобедренного треугольника позволяет находить решения и в более сложных ситуациях.
Интересные факты о равнобедренных треугольниках
ФактОписание
| 1. | В равнобедренном треугольнике два угла при основании равны между собой. |
| 2. | Высота, опущенная из вершины равнобедренного треугольника, делит его на два подобных треугольника и прямоугольник. |
| 3. | Медиана, проведенная из вершины равнобедренного треугольника к основанию, является биссектрисой угла при вершине и медианой прямоугольного треугольника, образованного медианой. |
| 4. | У равнобедренного треугольника сумма двух равных углов всегда равна 180 градусам. |
| 5. | Равнобедренный треугольник может быть и равносторонним треугольником. |
Равнобедренные треугольники являются интересным объектом изучения в математике и имеют множество свойств и особенностей. Изучая их, вы сможете узнать больше о геометрии и ее применении в повседневной жизни.
Вопрос-ответ:
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник, у которого две стороны равны между собой.
Как определить равнобедренный треугольник?
Чтобы определить, является ли треугольник равнобедренным, нужно проверить, равны ли две стороны этого треугольника. Если две стороны одинаковы, то треугольник является равнобедренным.
Какие свойства имеет равнобедренный треугольник?
У равнобедренного треугольника есть несколько свойств: у него две равные стороны, два равных угла и один угол, противолежащий равным сторонам, тоже равен.
Где можно встретить равнобедренные треугольники в реальной жизни?
Равнобедренные треугольники можно встретить в различных предметах и конструкциях, например, в знаках дорожного движения, строительных элементах, фигурах в геометрических рисунках.
Задачи для самостоятельного решения
1. Дан треугольник, у которого две стороны равны 5 см, а угол между ними равен 60 градусов. Найдите длину третьей стороны треугольника.
2. В равнобедренном треугольнике один из углов равен 45 градусов. Найдите значения остальных двух углов.
3. Известно, что основание равнобедренного треугольника равно 8 см, а боковая сторона равна 10 см. Найдите периметр треугольника.
4. В прямоугольном треугольнике один из углов равен 90 градусов, а гипотенуза равна 13 см. Найдите катет треугольника, если он равнобедренный.
5. У треугольника две стороны равны 7 см, а один из углов между ними равен 45 градусов. Найдите площадь треугольника.
6. В равнобедренном треугольнике высота, опущенная из вершины основания, равна 12 см. Найдите площадь треугольника, если длина основания равна 10 см.


Мне очень интересно узнать, что такое равнобедренный треугольник. Ведь математика — это такое увлекательное и полезное занятие! Равнобедренный треугольник имеет две равные стороны и два равных угла при основании. Это означает, что если мы соединим точку на вершине с серединой основания, то получим две равные боковые стороны. Мне кажется, что равнобедренные треугольники выглядят очень интересно и красиво. Когда я узнала об этом, я сразу начала искать такие треугольники вокруг себя. Теперь я вижу их везде: в окнах, дверях, деревьях и даже на упаковках продуктов! Математика — это такое удивительное открытие для меня, и я рада тому, что учусь в школе и узнаю все больше новых и интересных фактов. Буду ждать новых математических открытий!
Равнобедренный треугольник в математике является особым видом треугольника, который имеет две равные стороны и два равных угла. Это означает, что если мы возьмем линейку и измерим две стороны треугольника, то они окажутся одинаковой длины. Также, когда мы измерим углы треугольника, два из них окажутся одинаковыми. Это интересно, потому что равнобедренные треугольники имеют много свойств и особенностей. Одно из свойств равнобедренного треугольника заключается в том, что высота треугольника, проведенная из вершины противоположной равным сторонам, будет одновременно и медианой и биссектрисой этого треугольника. Это означает, что точка пересечения этой высоты с основанием будет одновременно делить основание треугольника на две равные части и делить угол между основанием и равными сторонами на две равные части. Еще одно интересное свойство равнобедренных треугольников — это то, что сумма двух равных углов всегда будет равна 180 градусов. Это можно проверить, просто сложив значения этих углов. Это свойство помогает нам решать задачи с равнобедренными треугольниками и находить значения углов в них. Равнобедренные треугольники встречаются не только в математике, но и в реальной жизни. Например, в шестиугольных звездах, в некоторых строительных конструкциях, а также в некоторых символах и знаках. Понимание равнобедренных треугольников помогает нам лучше понять и анализировать окружающий мир и применять математические знания на практике.
Замечательная статья! Я всегда была заинтересована в математике, и этот текст помог мне лучше понять, что такое равнобедренный треугольник. Оказывается, у него две равные стороны и два равных угла. Когда я училась в четвертом классе, мы только начинали изучать геометрию, и я помню, как интересно было изучать разные типы треугольников. Равнобедренные треугольники имеют особую симметрию, и это делает их особенно интересными. Я теперь смогу легко распознать их и использовать эту информацию для решения различных задач. Спасибо!
Равнобедренный треугольник в математике для 4 класса — это особый вид треугольника, у которого две стороны равны между собой. Такой треугольник получает свое название из-за того, что у него две равные «ноги». Например, если у нас есть треугольник ABC, то сторона AB будет равна стороне AC. Важно также отметить, что у равнобедренного треугольника углы при основании, то есть при равных сторонах, также равны между собой. Это свойство помогает нам решать различные задачи, связанные с равнобедренными треугольниками. Знание и понимание этого понятия поможет вам успешно справляться с заданиями по геометрии в 4 классе и будет полезным и в будущем.