Что такое равнобедренный треугольник 5 класс математика

Равнобедренный треугольник в математике 5 класса — это треугольник, у которого две стороны равны. Узнайте, как определить и классифицировать равнобедренные треугольники и решить задачи связанные с ними в пятом классе математики.

Равнобедренный треугольник — это треугольник, у которого две стороны равны. В 5 классе математики одной из важных тем является изучение геометрических фигур, в том числе треугольников. Равнобедренные треугольники являются одним из видов треугольников и имеют свои особенности и свойства.

Свойства равнобедренных треугольников:

1. У равнобедренного треугольника две стороны равны.
2. У равнобедренного треугольника два угла при основании (основания — это равные стороны) равны.
3. У равнобедренного треугольника высота, проведенная к основанию, является биссектрисой угла при вершине.

Примеры равнобедренных треугольников:

1. Треугольник со сторонами 5 см, 5 см и 3 см является равнобедренным, так как у него две стороны равны.

2. Треугольник со сторонами 12 мм, 12 мм и 8 мм является равнобедренным, так как у него две стороны равны.

Изучение равнобедренных треугольников позволяет углубить знания о геометрии и применить их на практике при решении задач. Знание свойств и примеров равнобедренных треугольников поможет ученикам успешно справиться с заданиями в школьных упражнениях и тестах.

Определение равнобедренного треугольника

Равнобедренные треугольники часто встречаются в природе и в повседневной жизни. Например, знакомый символ медицины — красный крест на белом фоне — представляет собой равнобедренный треугольник. Также равнобедренные треугольники используются в архитектуре, в конструкции мостов и в других областях.

Равнобедренные треугольники обладают некоторыми свойствами, которые можно использовать при решении задач. Например, в равнобедренном треугольнике высота, опущенная из вершины к основанию, является медианой и биссектрисой одновременно. Также в равнобедренном треугольнике углы при одинаковых сторонах равны между собой.

Свойства равнобедренного треугольника

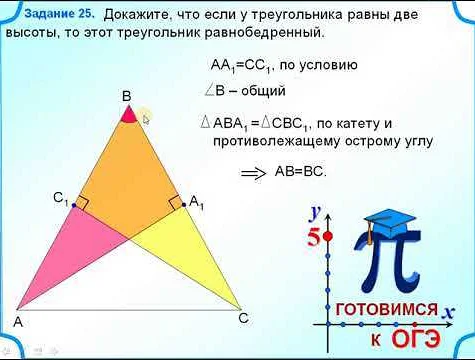
У равнобедренного треугольника есть несколько свойств:

1. Углы при основании равны по мере.
2. Угол, противолежащий основанию, равен.
3. Биссектриса угла, противолежащего основанию, является высотой и медианой этого треугольника.
4. Высота, опущенная из вершины, совпадает с биссектрисой угла, противолежащего основанию.
5. Медиана, проведенная из основания, совпадает с биссектрисой угла, противолежащего основанию.
6. Основание равнобедренного треугольника делит биссектрису угла, противолежащего основанию, на две равные части.

Равнобедренный треугольник можно проверить по заданным длинам его сторон. Если две стороны равны, то треугольник равнобедренный.

Примеры равнобедренных треугольников:

• Равнобедренный треугольник с боковыми сторонами длиной 6 см и основанием длиной 8 см.
• Равнобедренный треугольник с боковыми сторонами длиной 12 см и основанием длиной 10 см.
• Равнобедренный треугольник с боковыми сторонами длиной 5 см и основанием длиной 7 см.

Периметр равнобедренного треугольника

Периметр равнобедренного треугольника можно вычислить, сложив длины всех его сторон. В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона отличается от них.

Чтобы найти периметр равнобедренного треугольника, нужно умножить длину одной из равных сторон на 2 и добавить к этому результату длину третьей стороны. Формула для вычисления периметра равнобедренного треугольника выглядит следующим образом:

Периметр = 2 * a + b, где a — длина равных сторон, b — длина третьей стороны.

Например, если в равнобедренном треугольнике равные стороны имеют длину 5 см, а третья сторона — 7 см, то периметр можно вычислить следующим образом:

Длина стороныВычисления

5 см	2 * 5 = 10 см
7 см	10 + 7 = 17 см

Таким образом, периметр равнобедренного треугольника с равными сторонами длиной 5 см и третьей стороной длиной 7 см равен 17 см.

Высота равнобедренного треугольника

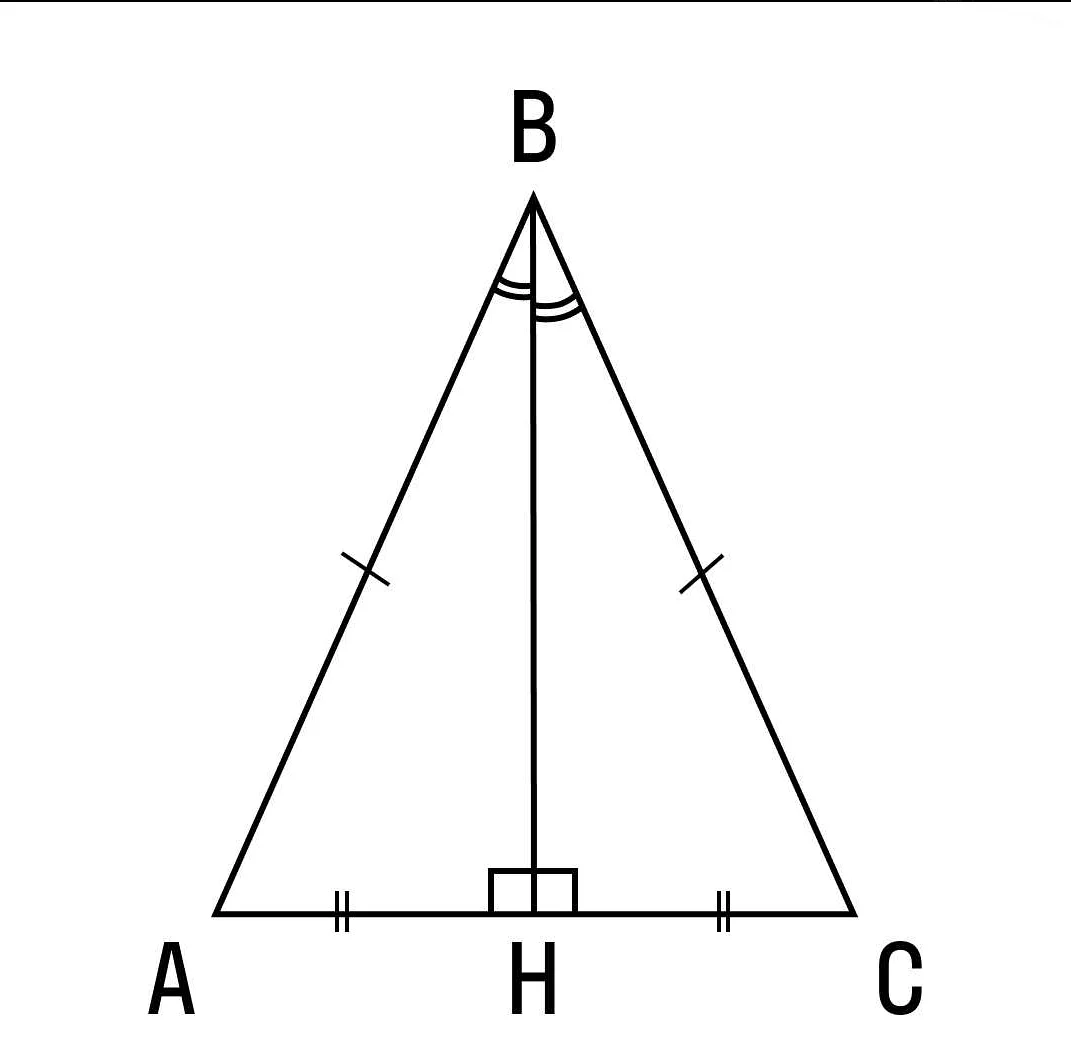
Свойства высоты равнобедренного треугольника:

• Высота равнобедренного треугольника делит его на два прямоугольных треугольника, каждый из которых является подобным исходному равнобедренному треугольнику.
• Высота равнобедренного треугольника является биссектрисой его вершины и медианой его основания.
• Высота равнобедренного треугольника равна половине длины основания.

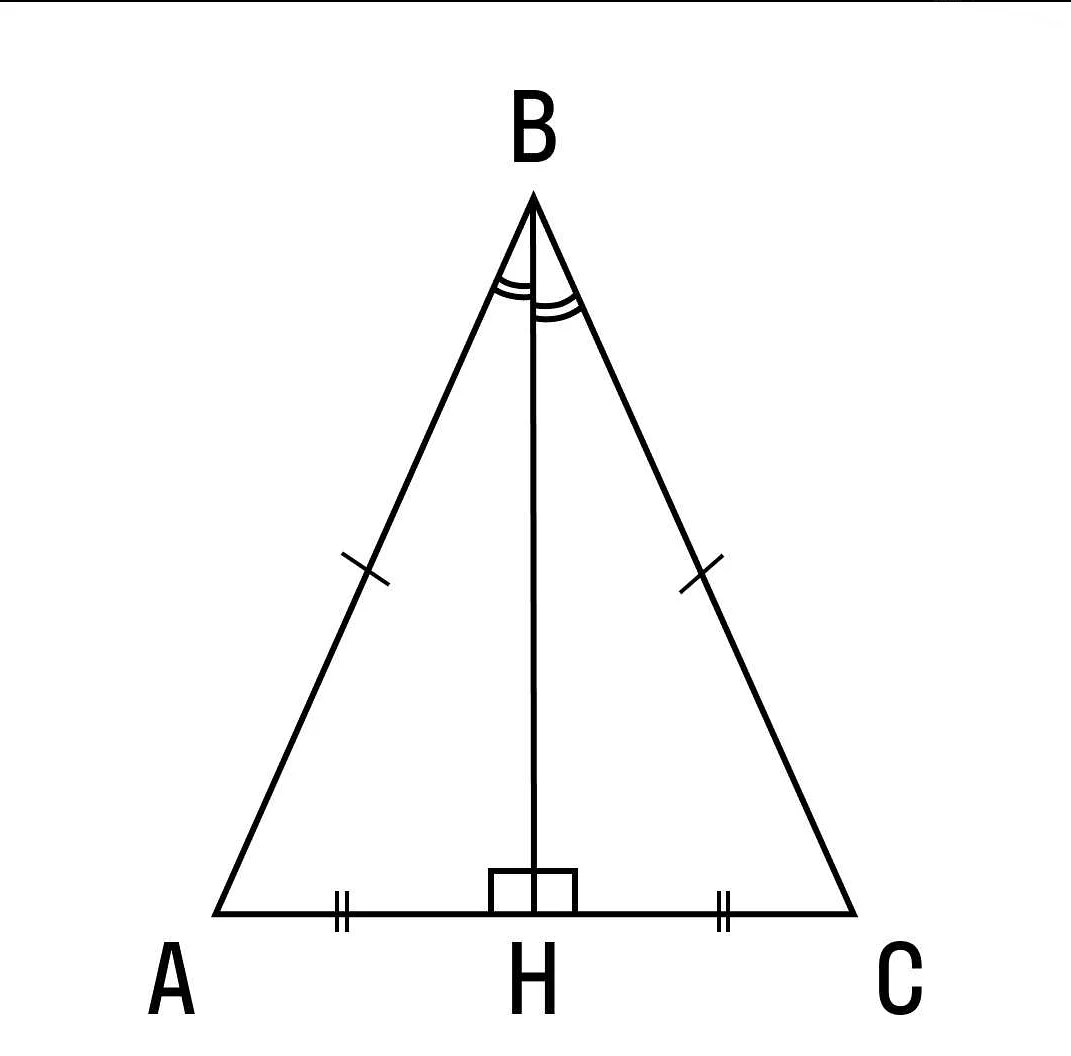
Пример: Дан равнобедренный треугольник ABC, в котором AB = AC. Пусть BD — высота, опущенная из вершины A на основание BC. Тогда BD будет являться биссектрисой угла BAC и медианой основания BC. Кроме того, BD = CD = 1/2 BC.

Медианы равнобедренного треугольника

В равнобедренном треугольнике медианы, проходящие через вершины равных сторон, делятся пополам. Это означает, что каждая из этих медиан делит противоположную сторону на две равные части.

Медианы, проходящие через основание равнобедренного треугольника, делятся таким образом, что одна часть равна третьей части; то есть, одна часть медианы равна сумме двух других частей.

Из свойств медиан можно вывести еще одно интересное свойство равнобедренного треугольника. Так как медианы делятся пополам, то точка их пересечения, называемая центром масс, находится на одинаковом расстоянии от всех трех вершин треугольника. Это значит, что центр масс равнобедренного треугольника лежит на оси симметрии треугольника.

Например, рассмотрим равнобедренный треугольник ABC, где AB = AC. Пусть M и N – середины сторон AB и AC соответственно. Тогда AM и AN – медианы равнобедренного треугольника ABC.

Таким образом, медианы равнобедренного треугольника являются важным свойством этой фигуры и являются линиями симметрии. Они делят стороны равнобедренного треугольника на равные части и пересекаются в центре масс треугольника.

Углы равнобедренного треугольника

Углы равнобедренного треугольника имеют следующие свойства:

СвойствоОписание

Основной угол	Угол, образованный двумя равными сторонами треугольника
Боковые углы	Углы, образованные одной из равных сторон и продолжением другой равной стороны треугольника
Боковые углы равны	Боковые углы равнобедренного треугольника всегда равны между собой
Основной угол половину разности двух боковых углов	Значение основного угла равно половине разности двух боковых углов

Например, в равнобедренном треугольнике с боковыми сторонами длиной 5 и основанием длиной 8, боковые углы будут равными, а значения основного угла будут равны половине разности двух боковых углов.

Теорема Пифагора для равнобедренного треугольника

В прямоугольном треугольнике с катетами, равными по длине, квадрат гипотенузы равен сумме квадратов катетов:

а² + а² = с²

где а — длина катета, с — длина гипотенузы.

Теорема Пифагора имеет свое расширение и для равнобедренных треугольников. Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой. Также в равнобедренном треугольнике два угла при основании равны между собой.

Теорема Пифагора для равнобедренного треугольника утверждает, что в таком треугольнике квадрат основания равен сумме квадратов половины основания и высоты:

а² = (b/2)² + h²

где а — длина основания, b — длина стороны треугольника, h — высота треугольника.

Теорема Пифагора для равнобедренного треугольника позволяет находить неизвестные стороны и высоту треугольника, если известны две из этих величин.

Рассмотрим пример для наглядности. Пусть у нас есть равнобедренный треугольник со стороной b = 5 и основанием а = 7. Нам нужно найти высоту h.

Подставляя известные значения в формулу теоремы Пифагора для равнобедренного треугольника, получаем:

7² = (5/2)² + h²

49 = 6.25 + h²

h² = 42.75

h ≈ √42.75 ≈ 6.53

Таким образом, высота равнобедренного треугольника с основанием 7 и стороной 5 примерно равна 6.53.

Примеры равнобедренных треугольников в жизни

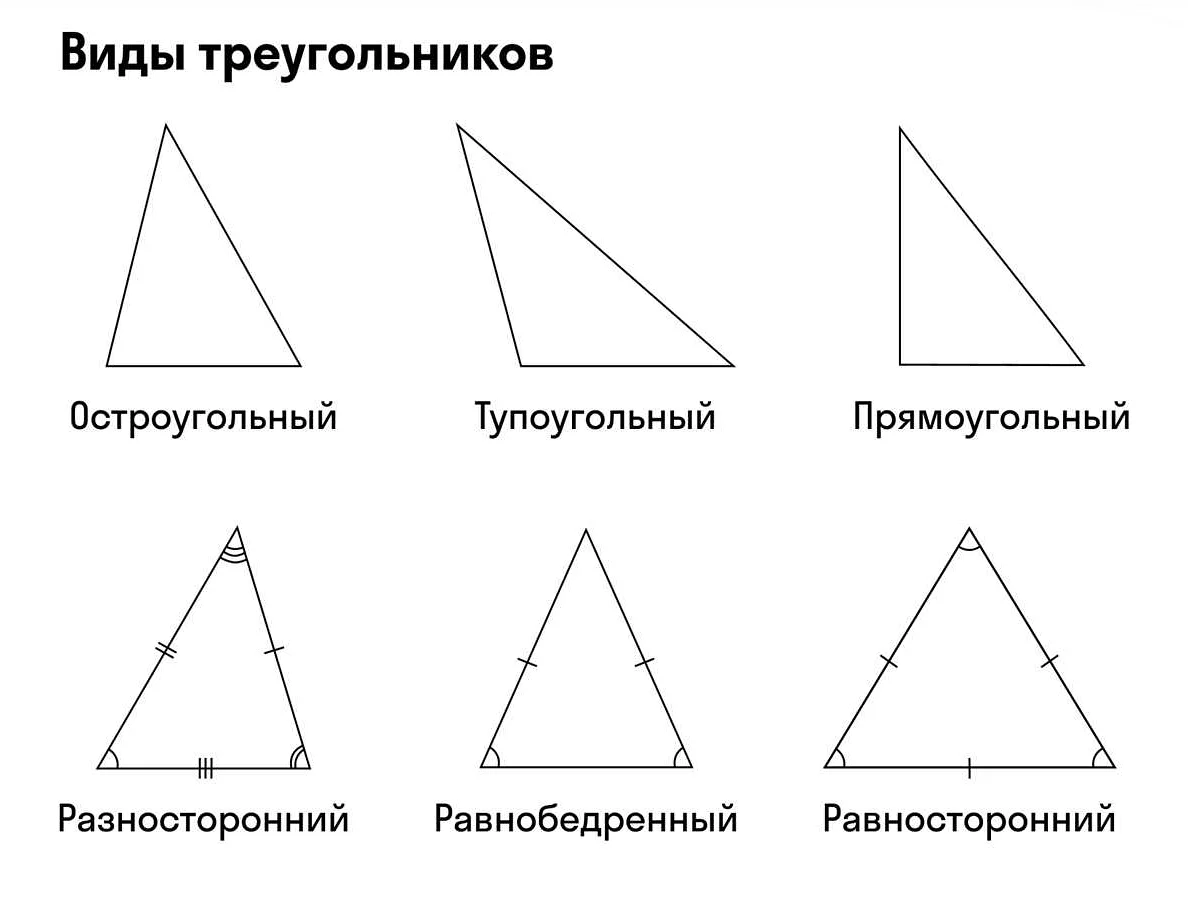
Равнобедренные треугольники встречаются в жизни очень часто. Вот некоторые примеры:

• Флаги многих стран имеют форму равнобедренного треугольника. Например, флаги Швейцарии, Японии и Непала.
• Крыши многих домов также имеют форму равнобедренного треугольника. Это позволяет сделать крышу более прочной и устойчивой.
• Многие пирамиды, как древние, так и современные, имеют форму равнобедренного треугольника.
• Арки мостов и некоторых зданий могут иметь форму равнобедренного треугольника.
• Форма некоторых островов и полуостровов тоже напоминает равнобедренный треугольник.

Это только некоторые примеры использования равнобедренных треугольников в жизни. Они встречаются в архитектуре, геометрии и географии. Изучение равнобедренных треугольников помогает нам лучше понять мир вокруг нас и использовать этот знакомый геометрический объект в различных областях нашей жизни.

Видео по теме:

Что такое равнобедренный треугольник?

Равнобедренный треугольник — это треугольник, у которого две стороны равны друг другу. Также у равнобедренного треугольника два угла при основании равны.

Как определить, является ли треугольник равнобедренным?

Для определения равнобедренности треугольника, необходимо проверить, равны ли две его стороны. Если да, то треугольник равнобедренный.