Что такое сопряжение в математике

Сопряжение в математике — это процесс, при котором к каждому элементу множества сопоставляется другой элемент с определенными свойствами. Узнайте, какое значение имеет сопряжение в различных областях математики и как оно используется для решения различных задач и проблем.

Сопряжение — это одно из ключевых понятий в алгебре и математическом анализе. Оно используется для описания отношения между комплексными числами и другими математическими объектами. Сопряжение позволяет получить новое число, которое является комплексно-сопряженным к исходному.

Комплексно-сопряженные числа имеют одинаковую действительную часть и противоположную мнимую часть. Например, если исходное число равно a + bi, то его комплексно-сопряженное число будет a — bi. Сопряжение можно представить в виде операции, которая меняет знак между мнимой и действительной частями числа.

Применение сопряжения в математике широко распространено. Оно используется в различных областях, таких как теория вероятностей, электротехника и физика. Например, в теории вероятностей сопряжение помогает вычислять вероятности событий, а в электротехнике — анализировать переменные токи и напряжения.

Примером использования сопряжения является вычисление модуля комплексного числа. Модуль — это расстояние от начала координат до точки, которая соответствует комплексному числу на комплексной плоскости. Для нахождения модуля комплексного числа требуется умножить его на сопряженное число и извлечь квадратный корень из результата.

Таким образом, сопряжение в математике играет важную роль при работе с комплексными числами и другими математическими объектами. Оно позволяет выполнять различные операции, такие как сложение, вычитание, умножение и деление комплексных чисел. Знание и понимание сопряжения является необходимым для успешного решения задач в различных областях математики и ее приложений.

Определение сопряжения в математике

Сопряжение комплексного числа изменяет знак только у мнимой части, оставляя действительную часть неизменной. Например, если комплексное число равно (3, 4), то его сопряженное число будет (-3, -4).

Сопряжение используется для решения различных математических задач и имеет несколько важных свойств. Например, сумма комплексного числа и его сопряженного числа всегда будет являться действительным числом, так как мнимая часть взаимно уничтожается. Также, произведение комплексного числа и его сопряженного числа будет равно квадрату модуля этого числа.

Сопряжение комплексных чисел также имеет геометрическую интерпретацию. Если представить комплексное число как точку на комплексной плоскости, то его сопряженное число будет отражением относительно вещественной оси.

Сопряжение в математике играет важную роль в различных областях, таких как алгебра, анализ, теория вероятностей и другие. Оно широко используется в комплексном анализе, где комплексные числа являются основным объектом изучения.

Примеры сопряжения в математике

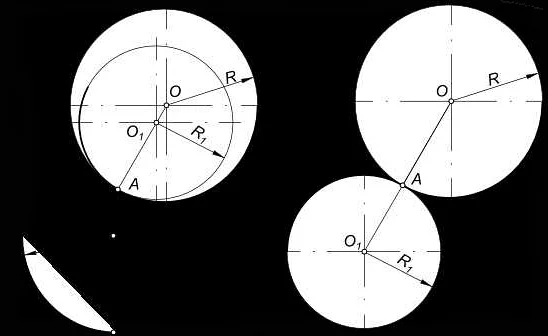
1. Сопряжение комплексного числа: для комплексного числа a + bi его сопряженным числом называется число a — bi. Сопряжение комплексного числа позволяет находить его модуль и делить комплексные числа.
2. Сопряжение матрицы: если дана матрица A размерности nxm, то сопряженной ей матрицей называется матрица B, полученная заменой каждого элемента a[i][j] на его комплексно-сопряженное значение.
3. Сопряжение вектора: векторное сопряжение позволяет найти вектор с противоположным направлением, но с такой же длиной. Это полезно, например, при решении задач на нахождение перпендикулярного вектора или при проведении векторных вычислений.
4. Сопряжение логического выражения: в логике сопряжение (отрицание) выражения позволяет получить истинность выражения, противоположное исходному.

Это лишь некоторые примеры использования сопряжения в математике. Оно широко применяется в алгебре, геометрии, теории вероятностей и других математических дисциплинах. Понимание сопряжения позволяет решать различные задачи и проводить вычисления с большей точностью и эффективностью.

Сопряжение и комплексные числа

Сопряженное число к комплексному числу a + bi представляется в виде a — bi. Иными словами, сопряжение меняет знак перед мнимой частью комплексного числа. Например, сопряженное число к 3 + 4i будет равно 3 — 4i.

Сопряжение комплексных чисел имеет ряд интересных свойств. Например, сумма комплексного числа и его сопряженного числа всегда будет действительным числом, так как мнимые части взаимно уничтожаются. Также, произведение комплексного числа и его сопряженного числа будет равно квадрату модуля комплексного числа.

Сопряжение комплексных чисел широко применяется в различных областях математики и физики. Например, при решении уравнений и систем уравнений, при анализе сигналов в теории сигналов, а также в комплексном анализе и теории вероятностей.

Сопряжение и геометрия

Симметричное отражение фигуры относительно заданной прямой или плоскости называется сопряжением. Это означает, что каждая точка фигуры отражается относительно оси симметрии и сохраняет свое положение. В результате получается симметричная фигура относительно оси или плоскости сопряжения.

Сопряжение имеет много применений в геометрии. Например, в прямоугольной системе координат сопряжение относительно осей координат используется для нахождения симметричной точки относительно начала координат.

Также сопряжение может быть использовано для нахождения симметричных относительно заданной прямой или плоскости фигур. Это может быть полезно при решении задач на построение геометрических фигур.

В геометрии сопряжение является одним из способов симметричного преобразования фигур. Оно позволяет сохранить форму и размеры фигуры, изменяя только ее положение относительно оси или плоскости сопряжения.

Таким образом, сопряжение является важным понятием в геометрии и находит широкое применение при решении задач, связанных с построением и анализом геометрических фигур.

Свойства сопряжения в математике

Сопряжение обладает несколькими важными свойствами:

1. 1. Сопряжение суммы двух комплексных чисел равно сумме их сопряжений:

conj(a + bi) = conj(a) + conj(bi) = a — bi

1. 1. Сопряжение произведения двух комплексных чисел равно произведению их сопряжений в обратном порядке:

conj((a + bi)(c + di)) = conj(a + bi) * conj(c + di) = (a — bi)(c — di)

1. 1. Сопряжение квадрата комплексного числа равно квадрату его сопряжения:

conj((a + bi)^2) = conj(a^2 + 2abi — b^2) = (a — bi)^2

1. 1. Сопряжение произведения комплексного числа на действительное число равно произведению сопряжения комплексного числа на это действительное число:

conj(k(a + bi)) = k * conj(a + bi) = k(a — bi)

1. 1. Сопряжение квадратного корня комплексного числа равно квадратному корню его сопряжения:

conj(sqrt(a + bi)) = sqrt(a — bi)

Эти свойства сопряжения в математике играют важную роль при работе с комплексными числами и находят применение в различных областях, включая физику, инженерию и информатику.

Применение сопряжения в математике

Комплексно сопряженное число получается путем изменения знака мнимой части исходного комплексного числа. Данная операция широко применяется в алгебре, геометрии и теории чисел.

Сопряжение также используется для нахождения корней многочленов с комплексными коэффициентами. Комплексные корни многочленов могут быть найдены путем нахождения корней сопряженного многочлена.

В анализе и математическом анализе сопряжение используется для нахождения сопряженной функции. При сопряжении функции меняются мнимые компоненты, что позволяет рассматривать сопряженную функцию в более удобной форме.

Сопряжение также применяется в физике, особенно в электронике и теории сигналов. Комплексно сопряженные числа используются для моделирования физических процессов, а сопряженные функции — для анализа сигналов и систем.

Таким образом, сопряжение является важным инструментом в математике и широко применяется в различных областях, где требуется анализ комплексных чисел, функций и процессов.

Сопряжение и алгебраические уравнения

Сопряженное число имеет ряд интересных свойств. Например, сумма числа и его сопряжения всегда является вещественным числом. Также, произведение числа на его сопряжение равно квадрату модуля этого числа. Это свойства широко используются при решении алгебраических уравнений.

При решении алгебраических уравнений, в которых присутствуют комплексные числа, часто требуется найти все корни уравнения. Если один из корней найден, то его сопряжение также является корнем уравнения. Используя это свойство, можно найти все корни путем перебора их сопряжений.

Например, рассмотрим уравнение \(x^2 — 5x + 6 = 0\). Его корнями являются числа 2 и 3. Их сопряжения соответственно равны 2 и 3. Таким образом, все корни уравнения найдены.

КореньСопряжение

2	2
3	3

Таким образом, сопряжение чисел позволяет найти все корни алгебраических уравнений и является важным инструментом в алгебре.

Значение сопряжения в других областях науки

Понятие сопряжения не ограничивается только математикой, оно также находит применение в различных областях науки. В следующей таблице представлены некоторые примеры использования сопряжения в разных научных дисциплинах:

Область наукиПример сопряженияЗначение

Физика	Комплексно-сопряженное сопротивление	Позволяет описывать переход энергии от активной составляющей к реактивной составляющей и наоборот в электрических цепях.
Химия	Сопряженные связи	Позволяют описывать особенности строения и свойств органических молекул, основанные на конъюгации пи-электронных областей.
Биология	Сопряженная транспортная цепь	Обеспечивает передачу энергии в процессе фотосинтеза и клеточного дыхания.
Лингвистика	Сопряжение гласных	Описывает явление смешения звуков при произношении слов и формировании слогов.

Это лишь некоторые примеры использования понятия сопряжения в разных научных областях. В каждой из них оно имеет свое специфическое значение и применение, что подчеркивает его универсальность и важность в научном исследовании.

Видео по теме:

Что такое сопряжение в математике?

Сопряжение в математике — это операция, которая изменяет знак мнимой части комплексного числа. Если комплексное число записано в виде a + bi, то его сопряженным числом будет a — bi.

Как можно представить сопряжение математически?

Сопряжение математически можно представить с помощью знака минус перед мнимой частью комплексного числа. Если число записано в виде a + bi, то его сопряженным числом будет a — bi.

Что такое сопряжение в математике?

Сопряжение в математике — это операция, при которой каждому комплексному числу a + bi сопоставляется его сопряженное число a — bi. В результате сопряжения меняется только знак мнимой части числа, а вещественная часть остается неизменной.