Что значит степень в математике
Содержимое
Степень в математике — это арифметическая операция, которая позволяет возводить число в степень. Степень может быть положительной, отрицательной или нулевой. В данной статье рассмотрим понятие степени, ее свойства и примеры использования в математике и реальной жизни.
Степень — это математическая операция, которая позволяет возвести число в определенную степень. В степень можно возвести любое число, но степень чаще всего используется для работы с целыми числами. Операция степени обозначается с помощью знака «^». Например, число 2 в степени 3 записывается как 2^3 и равно 8.
Степень имеет два основных компонента: основание и показатель. Основание — это число, которое возводится в степень. Показатель — это число, на которое возводится основание. В примере 2^3, 2 — это основание, а 3 — показатель.
В математике степени могут быть положительными, отрицательными и нулевыми. Положительные степени означают, что число умножается само на себя заданное количество раз. Например, 2^3 = 2 * 2 * 2 = 8. Отрицательные степени означают, что число становится дробным. Например, 2^-3 = 1 / (2 * 2 * 2) = 1/8. Нулевая степень всегда равна 1, кроме случая, когда основание равно нулю.
Примеры использования степени:
1. Возведение в положительную степень: 4^2 = 4 * 4 = 16
2. Возведение в отрицательную степень: 5^-2 = 1 / (5 * 5) = 1/25
3. Возведение в нулевую степень: 6^0 = 1
Использование степени позволяет упростить вычисления и работать с большими числами. Операция степени широко применяется в математике, физике, экономике и других науках.
Определение степени
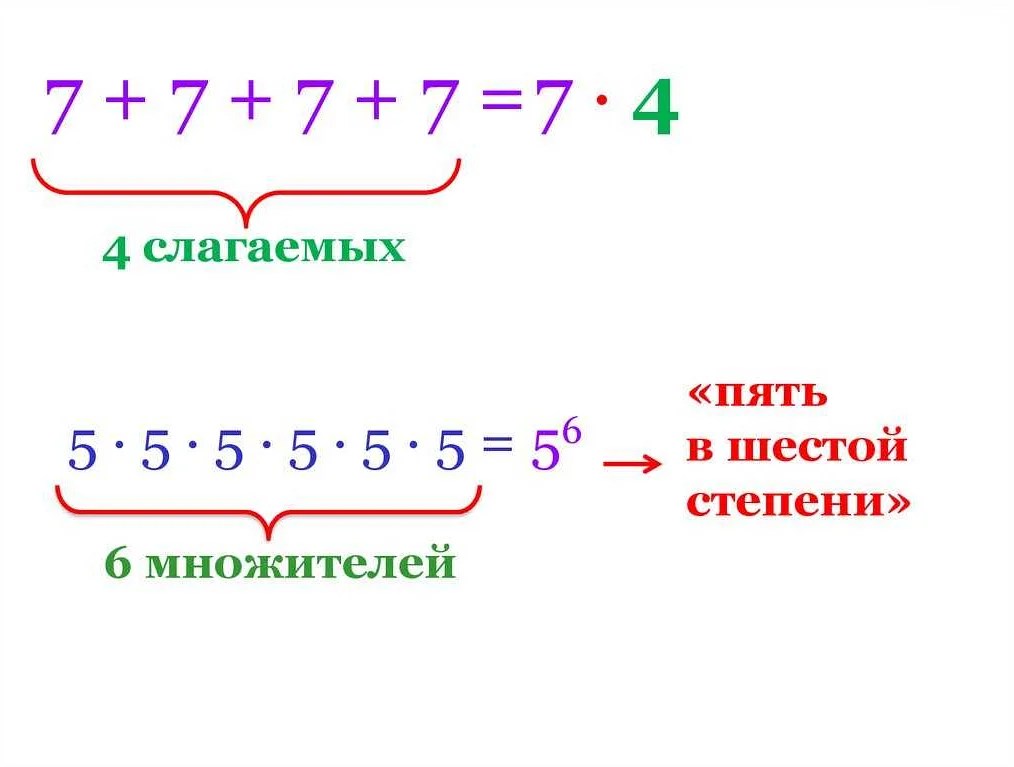
Степень обозначается с помощью символа «^». Например, 2^3 означает, что число 2 возводится в третью степень.
Пример: 2^3 = 2 * 2 * 2 = 8.
В математике также используются отрицательные и дробные степени. Отрицательная степень обратна положительной. Например, 2^(-2) = 1/(2^2) = 1/4 = 0.25. Дробная степень равна корню из основания. Например, 2^(1/2) = √2 ≈ 1.414.
Степень является важным понятием в математике и широко используется в различных областях, включая алгебру, геометрию, физику, экономику и другие.
Видео по теме:
Основание и показатель степени

Основание — это число, которое возводится в степень. Оно может быть любым вещественным числом или даже комплексным числом.
Примеры:
- В степени 2 основанием является число 3. Такая степень записывается как 3^2.
- В степени 3/2 основанием может быть, например, число 4. Такая степень записывается как 4^(3/2).
- В степени -1 основанием может быть число 2. Такая степень записывается как 2^(-1).
Показатель — это число, на которое возводится основание. Он может быть любым вещественным числом, но обычно является целым числом или рациональной дробью.
Примеры:
- В степени 2 показателем является число 2. Такая степень записывается как 3^2.
- В степени 3/2 показателем является число 3/2. Такая степень записывается как 4^(3/2).
- В степени -1 показателем является число -1. Такая степень записывается как 2^(-1).
Основание и показатель степени могут быть положительными, отрицательными или даже нулевыми числами. Все эти случаи имеют свои особенности и правила, которые определяют результат операции возведения в степень.
Примеры степеней
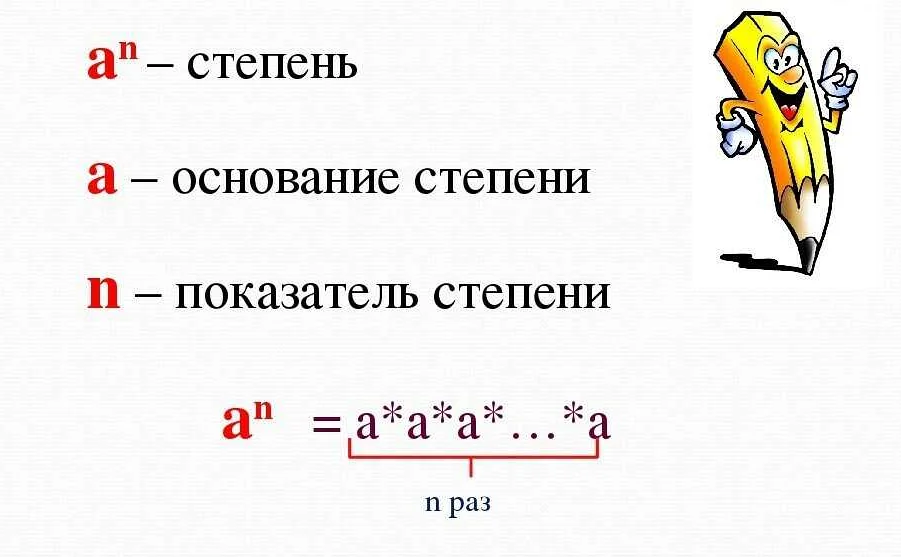
- 2 в степени 3 равно 2 * 2 * 2 = 8
- 5 в степени 2 равно 5 * 5 = 25
- 10 в степени 0 равно 1
- 3 в степени 4 равно 3 * 3 * 3 * 3 = 81
В этих примерах, число, которое возводится в степень, называется основанием, а число, указанное в верхнем индексе, называется показателем степени.
Вопрос-ответ:
Что такое степень в математике?
Степень в математике — это операция, которая позволяет возвести число в некоторую степень. В степени число, называемое основанием, умножается само на себя определенное количество раз, указанное в показателе степени.
Как записывается степень в математике?
Степень в математике записывается с помощью знака возведения в степень (^) и двух чисел: основания и показателя степени. Основание ставится внизу, а показатель степени — вверху. Например, 3^2 читается как «3 в степени 2» и означает, что число 3 нужно умножить само на себя 2 раза.
Какую роль играет показатель степени?
Показатель степени определяет, сколько раз нужно умножить число основание на себя. Например, в степени 2 основание умножается на себя 2 раза, в степени 3 — 3 раза и так далее.
Есть ли особые свойства степени?
Да, степень обладает несколькими свойствами. Например, если возвести число в степень 0, то результат будет равен 1. Если возвести 1 в любую степень, результат также будет равен 1. Также существуют правила умножения и деления степеней с одним и тем же основанием.
Можете привести примеры использования степени в математике?
Конечно! Например, если нужно найти площадь квадрата со стороной 3 см, нужно возвести это число в степень 2: 3^2 = 9 (см^2). Еще один пример — расчет интереса по вкладу с помощью формулы сложных процентов: A = P(1 + r/n)^(nt), где Р — сумма вклада, r — годовая процентная ставка, n — количество начислений процентов в год, t — срок вклада. В данном случае основание (1 + r/n) возводится в степень nt.
Свойства степеней
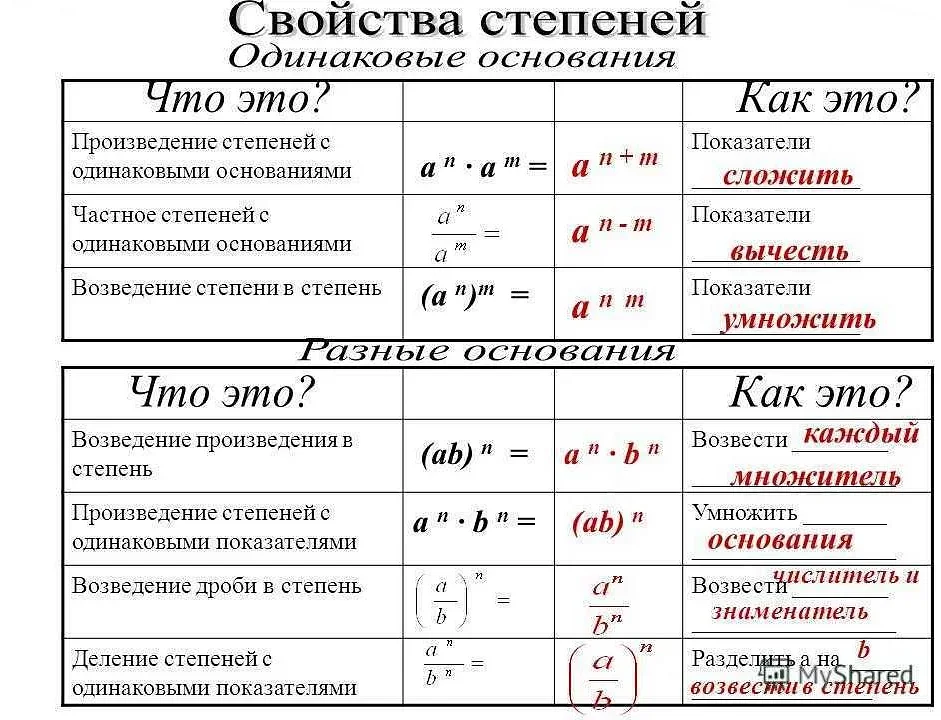
1. Свойство умножения степеней: чтобы умножить два числа, возведенные в степень, с одинаковыми основаниями, достаточно сложить их показатели степени. Например, am * an = am + n.
2. Свойство деления степеней: чтобы разделить два числа, возведенные в степень, с одинаковыми основаниями, необходимо вычесть показатель степени делителя из показателя степени делимого. Например, am / an = am — n.
3. Свойство возведения степени в степень: чтобы возвести число, возведенное в степень, в еще одну степень, необходимо умножить показатели степеней. Например, (am)n = am * n.
4. Свойство степени с показателем 0: любое число, возведенное в степень с показателем 0, равно 1. Например, a0 = 1.
5. Свойство степени с отрицательным показателем: любое число, возведенное в степень с отрицательным показателем, равно обратному числу, возведенному в положительную степень. Например, a-n = 1 / an.
Эти свойства помогают упростить вычисления и работу с числами, возведенными в степень. Они также могут быть использованы для решения различных задач и уравнений, связанных со степенями. Знание этих свойств позволяет уверенно оперировать степенями и использовать их в различных математических операциях.
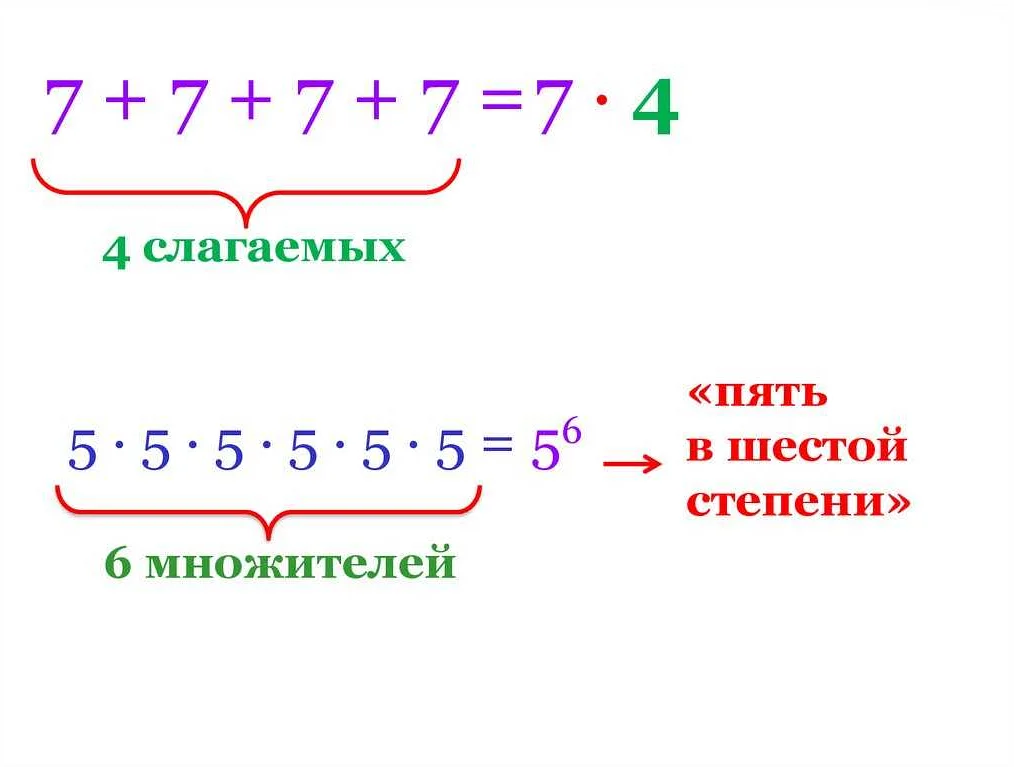
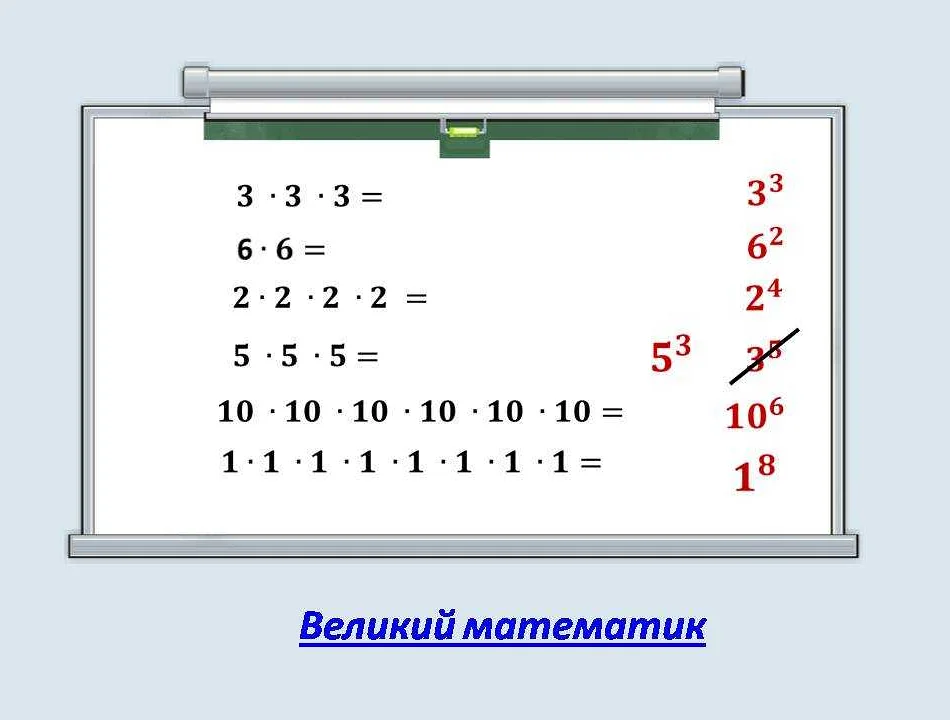
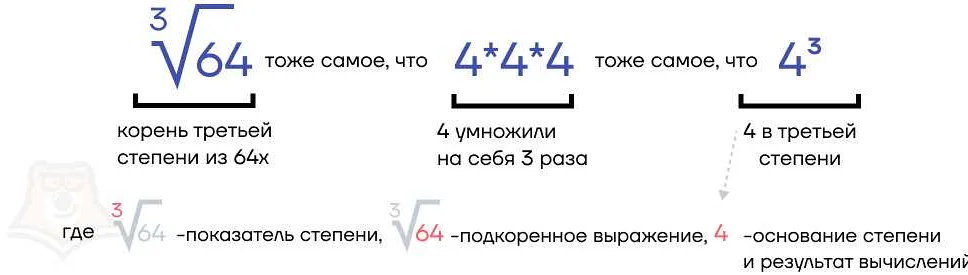
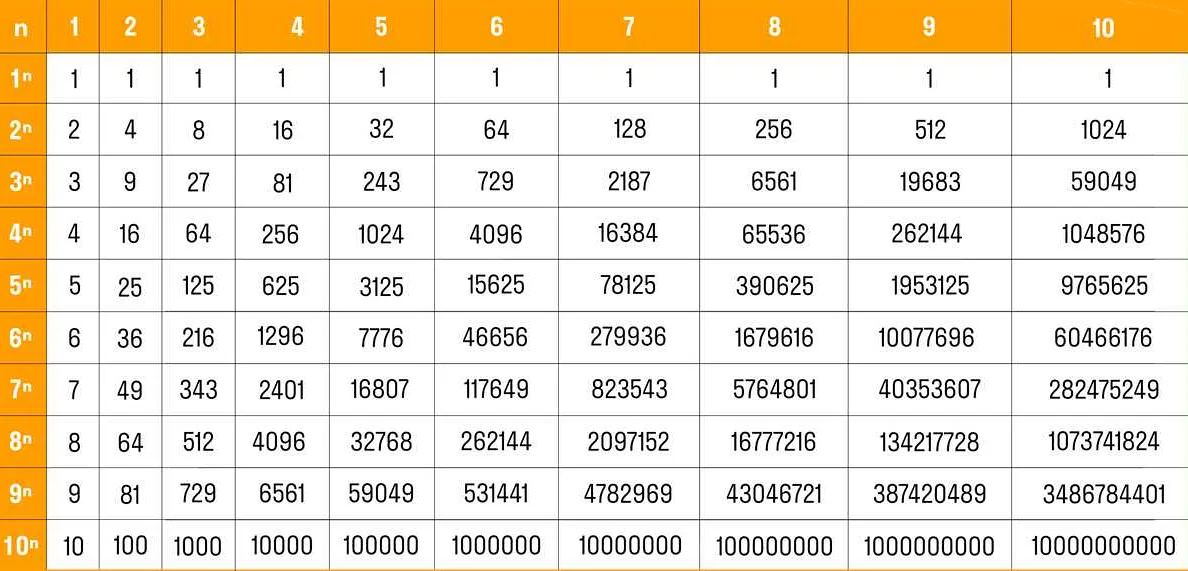
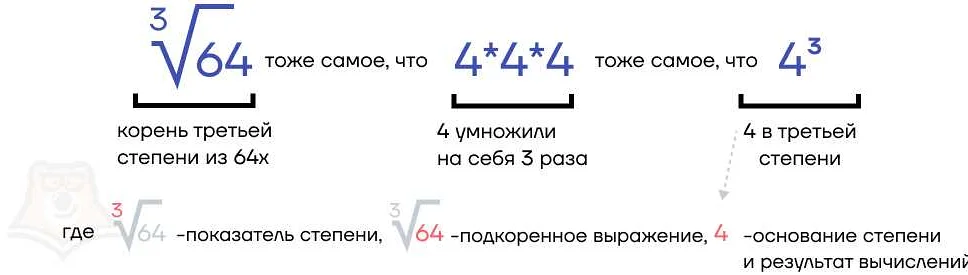
Степень в математике – это способ возводить число в определенную степень, то есть умножать его само на себя заданное количество раз. Важно понимать, что степень может быть не только целой, но и дробной или даже отрицательной. Это позволяет нам расширить возможности математических операций и решать различные задачи. Например, степень 2 возводит число в квадрат, а степень 0 является особенной, так как она равна единице. Благодаря степеням мы можем быстро и эффективно решать задачи, связанные с умножением и делением чисел. Поэтому понимание и применение степеней является важной частью математической грамотности.
Статья очень понятно и доступно объясняет, что такое степень в математике. Я всегда слышала этот термин, но никогда не понимала его смысл. Теперь я поняла, что степень — это когда число умножается само на себя несколько раз. Например, 2 в степени 3 равно 8, потому что 2 умножается само на себя три раза. Мне понравилось, что в статье приведены примеры и объяснение, как считать степени. Я думаю, что такие знания пригодятся мне в повседневной жизни и в дальнейшем изучении математики. Спасибо автору за простое и понятное объяснение!