Что такое сумма разность произведение частное в математике правило

Сумма, разность, произведение и частное — основные арифметические операции в математике. Узнайте, как правильно применять правило суммы, разности, произведения и частного в вычислениях и решении задач.

Математика — это наука, изучающая числа, их свойства и взаимоотношения. В рамках математики, основные операции над числами включают сложение, вычитание, умножение и деление. Понимание и умение применять правила данных операций является основой для решения различных математических задач и проблем.

Сумма — это результат операции сложения двух или более чисел. Для сложения чисел существуют определенные правила, которые позволяют определить их сумму. Например, сумма двух чисел равна их алгебраической сумме, то есть сумме их значений, причем знаки чисел могут быть как одинаковыми, так и противоположными.

Разность — это результат операции вычитания одного числа из другого. При вычитании чисел также существуют определенные правила. Например, при вычитании чисел, знаки чисел могут быть как одинаковыми, так и противоположными, а разность равна разности их значений.

Произведение — это результат операции умножения двух или более чисел. Правила умножения также определены. Например, при умножении чисел, знаки чисел могут быть как одинаковыми, так и противоположными, а произведение равно произведению их значений.

Частное — это результат операции деления одного числа на другое. Правила деления также определены. Например, частное двух чисел равно их отношению, причем знаки чисел могут быть как одинаковыми, так и противоположными.

Важно понять, что знание и применение правил сложения, вычитания, умножения и деления является необходимым для решения различных математических задач и обеспечивает понимание основных операций над числами.

В заключение, сумма, разность, произведение и частное являются основными операциями над числами в математике. Знание правил и определений этих операций необходимо для успешного решения математических задач и развития математического мышления.

Сумма, разность, произведение и частное в математике: правила и определения

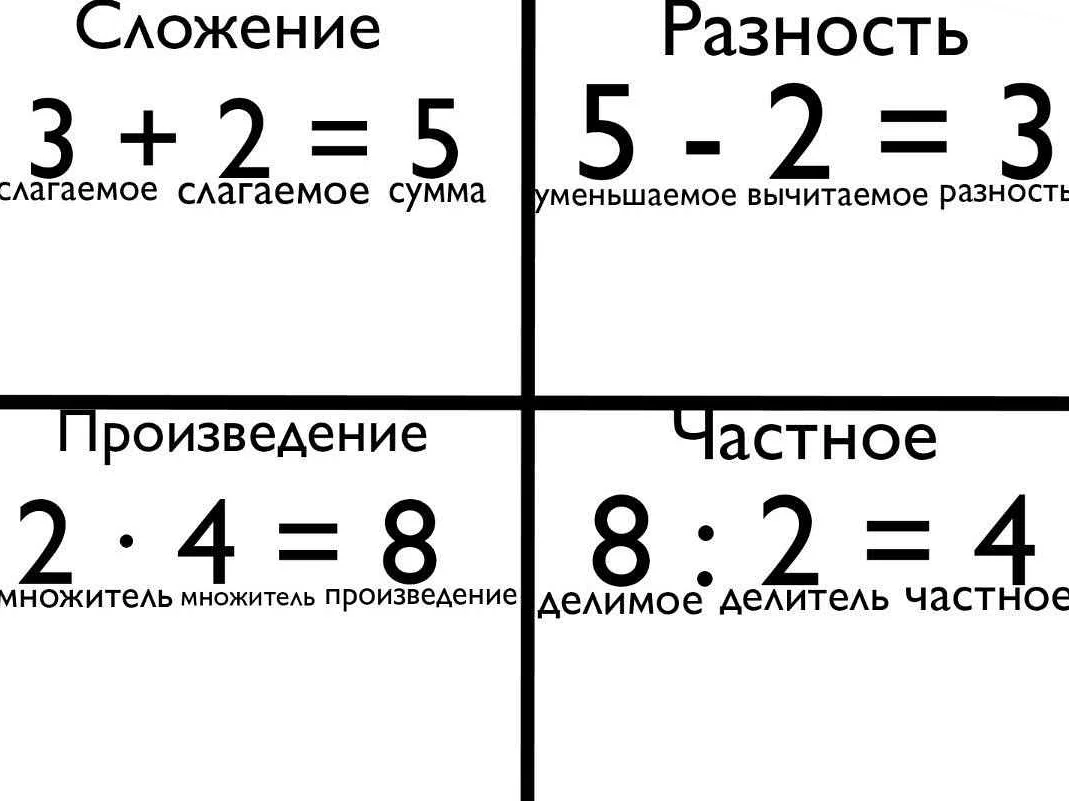
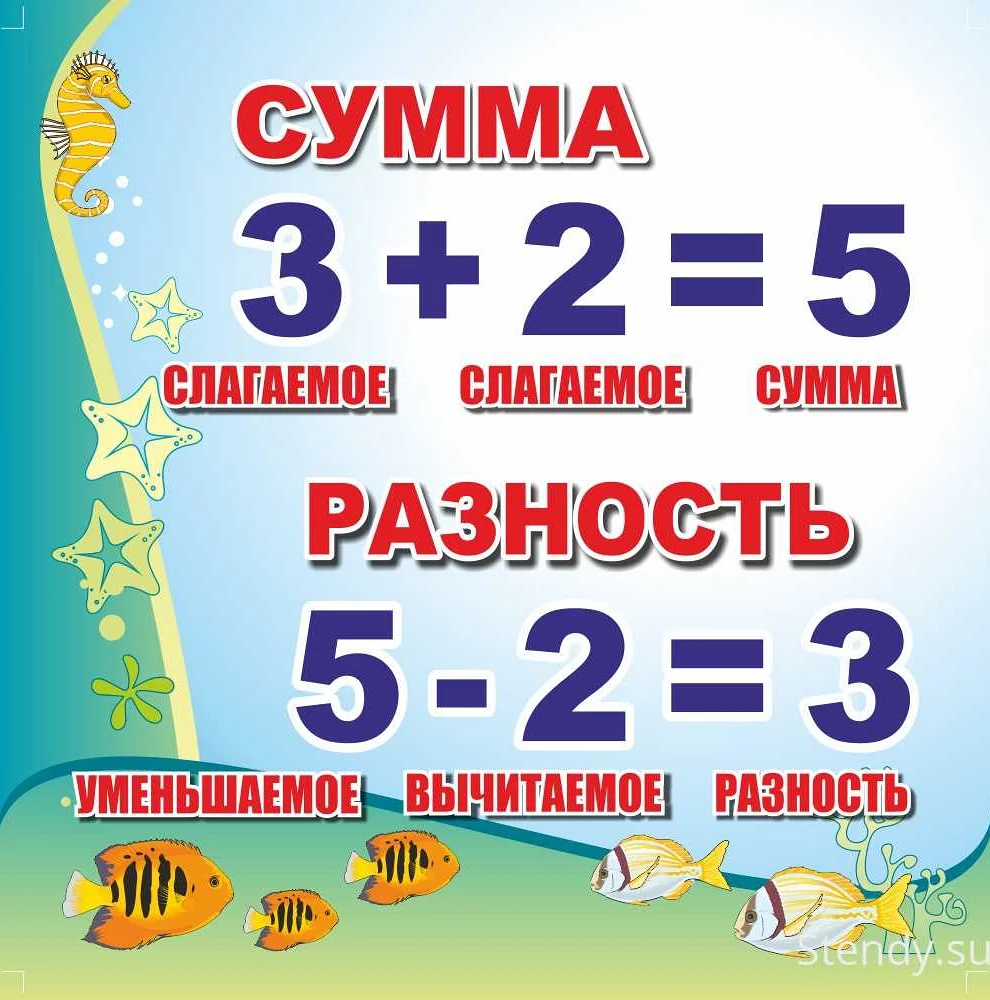
Сумма двух чисел — это результат их объединения. Например, сумма чисел 2 и 3 равна 5.

Разность двух чисел — это разница между ними. Например, разность чисел 5 и 3 равна 2.

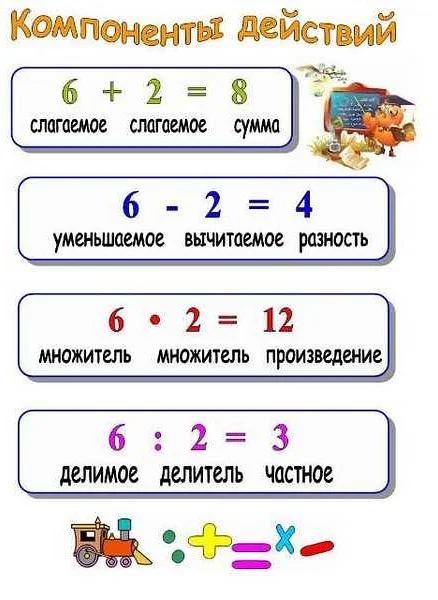
Произведение двух чисел — это результат их умножения. Например, произведение чисел 2 и 3 равно 6.

Частное двух чисел — это результат их деления. Например, частное чисел 6 и 3 равно 2.

При выполнении арифметических операций есть определенные правила:

• При сложении и умножении порядок чисел не имеет значения: a + b = b + a, a * b = b * a
• При вычитании и делении порядок чисел имеет значение: a — b ≠ b — a, a / b ≠ b / a
• При выполнении нескольких операций в одном выражении следует придерживаться законов приоритета: сначала выполняются операции умножения и деления, а затем сложения и вычитания

Таким образом, сумма, разность, произведение и частное позволяют нам выполнять арифметические операции и работать с числами, что является важной частью математики.

Видео по теме:

Определение суммы в математике

Для нахождения суммы чисел их необходимо сложить. Сумма обозначается символом «+» и записывается в виде a + b, где a и b — слагаемые.

При сложении чисел можно менять порядок слагаемых, при этом сумма остается неизменной. Например, a + b = b + a.

Сумма может быть расчитана как для натуральных чисел, так и для рациональных, вещественных и комплексных чисел. Также сумма может быть вычислена для бесконечных последовательностей чисел.

Сумма является одной из основных операций в математике и используется во многих областях, включая алгебру, арифметику и математический анализ.

Например, сумма двух чисел a = 3 и b = 4 будет равна 7: 3 + 4 = 7.

Пример:

Найдем сумму чисел 2, 5 и 7.

2 + 5 + 7 = 14

Таким образом, сумма чисел позволяет получить результат объединения двух или более чисел в одно число.

Правила сложения чисел

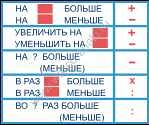
Основное правило сложения гласит: для сложения двух чисел нужно их поставить вместе и просуммировать. Например, для сложения чисел 3 и 5, нужно поставить их друг под другом и сложить соответствующие цифры:

3

+ 5

—

8

В данном примере первая цифра 3 складывается с первой цифрой 5, что дает результат 8. При сложении чисел обычно ставятся вертикальные линии между слагаемыми и под результатом, чтобы обозначить операцию сложения.

При сложении чисел с разным количеством цифр, нужно выравнять их по правому краю. Например, для сложения чисел 23 и 7:

23

+ 7

—-

30

В данном примере первая цифра 3 складывается с первой цифрой 7, что дает результат 10. Затем вторая цифра 2 просто переносится в результат без изменений.

Сложение чисел можно выполнять как в уме, так и на бумаге. Важно придерживаться правил сложения и быть внимательным при вычислении результатов.

Вопрос-ответ:

Что такое сумма в математике?

Сумма в математике — это результат действия сложения двух или более чисел. Для сложения чисел существуют определенные правила, которые позволяют получить точный результат.

Как определить разность двух чисел?

Разность двух чисел — это результат вычитания одного числа из другого. Для вычитания чисел существуют определенные правила. Разность можно определить, вычитая число, которое нужно вычесть, из числа, из которого нужно вычесть.

Что такое произведение в математике?

Произведение в математике — это результат действия умножения двух или более чисел. Умножение чисел также имеет определенные правила, которые нужно применять для получения точного результата.

Как определить частное двух чисел?

Частное двух чисел — это результат деления одного числа на другое. Для деления чисел также существуют правила. Частное можно определить, разделив число, которое нужно разделить, на число, на которое нужно разделить.

Определение разности в математике

Математически разность двух чисел a и b вычисляется следующим образом: a — b = c, где a и b — числа, а c — разность.

Разность может быть как положительной, так и отрицательной. Если a больше b, то разность будет положительной числом. Если a меньше b, то разность будет отрицательной числом. Если a равно b, то разность будет равна нулю.

Первое число (a)Второе число (b)Разность (a — b)

7	3	4
5	8	-3
10	10	0

Правила вычитания чисел

Правила вычитания чисел:

1. Вычитаемое всегда вычитается из вычитателя. Например, для выражения 8 — 3, число 3 является вычитаемым, а число 8 — вычитателем.
2. При вычитании цифр столбиком начинаем справа и двигаемся слева. Начинаем с вычитания последних разрядов чисел, затем переходим к следующим разрядам.
3. Если вычитаемое меньше вычитателя, то результат будет отрицательным числом. Например, 5 — 8 = -3.
4. Если вычитаемое равно нулю, то результат будет равен вычитателю. Например, 7 — 0 = 7.
5. При вычитании числа из нуля, результат будет равен отрицательному числу, равному вычитаемому. Например, 0 — 9 = -9.

Правила вычитания чисел позволяют нам корректно вычислять разности и получать правильные результаты.

Определение произведения в математике

Произведение двух чисел можно интерпретировать как операцию повторного сложения. Например, произведение 3 и 4 равно 12, что означает, что если сложить число 3 четыре раза, то получится число 12.

Определение произведения также распространяется на более чем два числа. В этом случае произведение всех чисел вычисляется путем последовательного умножения каждого числа с предыдущим результатом.

Произведение имеет несколько свойств, таких как ассоциативность (порядок умножения не влияет на результат), коммутативность (порядок сомножителей не важен) и дистрибутивность (умножение можно распределить на сложение и вычитание).

Правила умножения чисел

Основные правила умножения чисел:

1. Умножение числа на ноль всегда дает ноль. То есть, если один из множителей равен нулю, то и произведение будет равно нулю.
2. Умножение числа на единицу не изменяет значение числа. Если один из множителей равен единице, то и произведение будет равно другому множителю.
3. Умножение чисел коммутативно. То есть, порядок множителей не влияет на результат операции. Например, 2 умножить на 3 будет равно 3 умножить на 2.
4. Умножение чисел ассоциативно. То есть, порядок выполнения операций умножения не влияет на результат. Например, при умножении трех чисел a, b и c результат будет одинаковым, независимо от того, какой из множителей будет умножаться первым.
5. Для умножения чисел с разными знаками, результат будет отрицательным числом. Например, умножение положительного числа на отрицательное даст отрицательное произведение, и наоборот.
6. Для умножения чисел с одинаковыми знаками, результат будет положительным числом. Например, умножение двух положительных чисел или двух отрицательных чисел даст положительное произведение.

Правила умножения чисел помогают выполнять операцию умножения правильно и получать верные результаты. Они являются основой для более сложных математических операций и применяются во многих областях, включая физику, экономику и программирование.

Определение частного в математике

Чтобы найти частное, нужно разделить делимое на делитель. Например, если делимое равно 10, а делитель равен 2, то частное будет равно 5, так как 10 разделить на 2 равно 5.

Частное может быть как целым числом, так и десятичной дробью. Если результат деления является целым числом, то частное называется целочисленным. Если результат деления является десятичной дробью, то частное называется десятичным.

Важно понимать, что деление на ноль не определено в математике. Поэтому, если делитель равен нулю, то частное не существует.

Правила деления чисел

В математике существуют определенные правила деления чисел:

1. Если делитель равен нулю, то деление невозможно. Это правило называется «нельзя делить на ноль».
2. Если делимое равно нулю, то результат деления также будет нулем. Это правило называется «ноль делится на любое число равно нулю».
3. Если делимое и делитель одного знака, то результат деления будет положительным числом. Например, 6 делить на 2 равно 3.
4. Если делимое и делитель разных знаков, то результат деления будет отрицательным числом. Например, -6 делить на 2 равно -3.
5. Если делимое равно нулю, а делитель отличен от нуля, то результат деления будет нулем. Например, 0 делить на 5 равно 0.
6. Если делитель равен делимому, то результат деления будет равен единице. Например, 4 делить на 4 равно 1.

Правила деления чисел помогают понять, какие результаты получаются при выполнении данной операции и обеспечивают правильное решение математических задач.