Что такое произведение и частное сумма и разность в математике

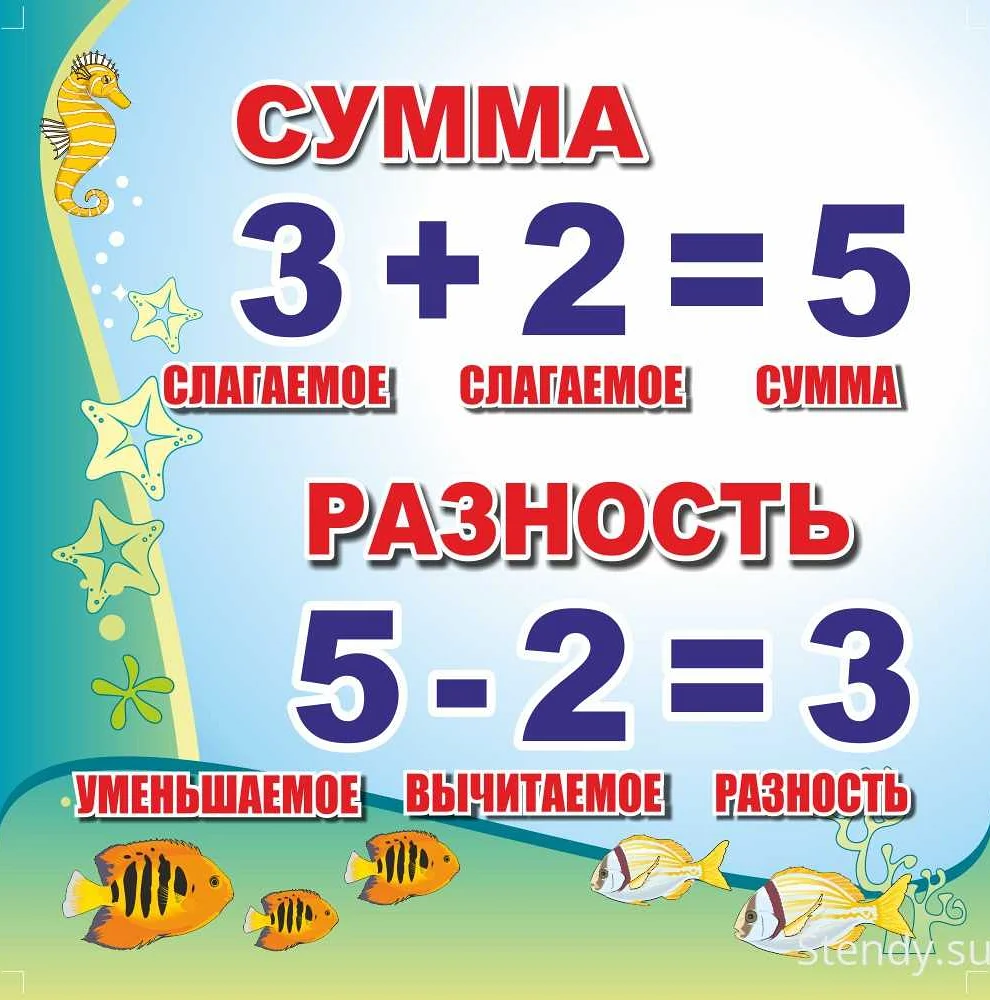
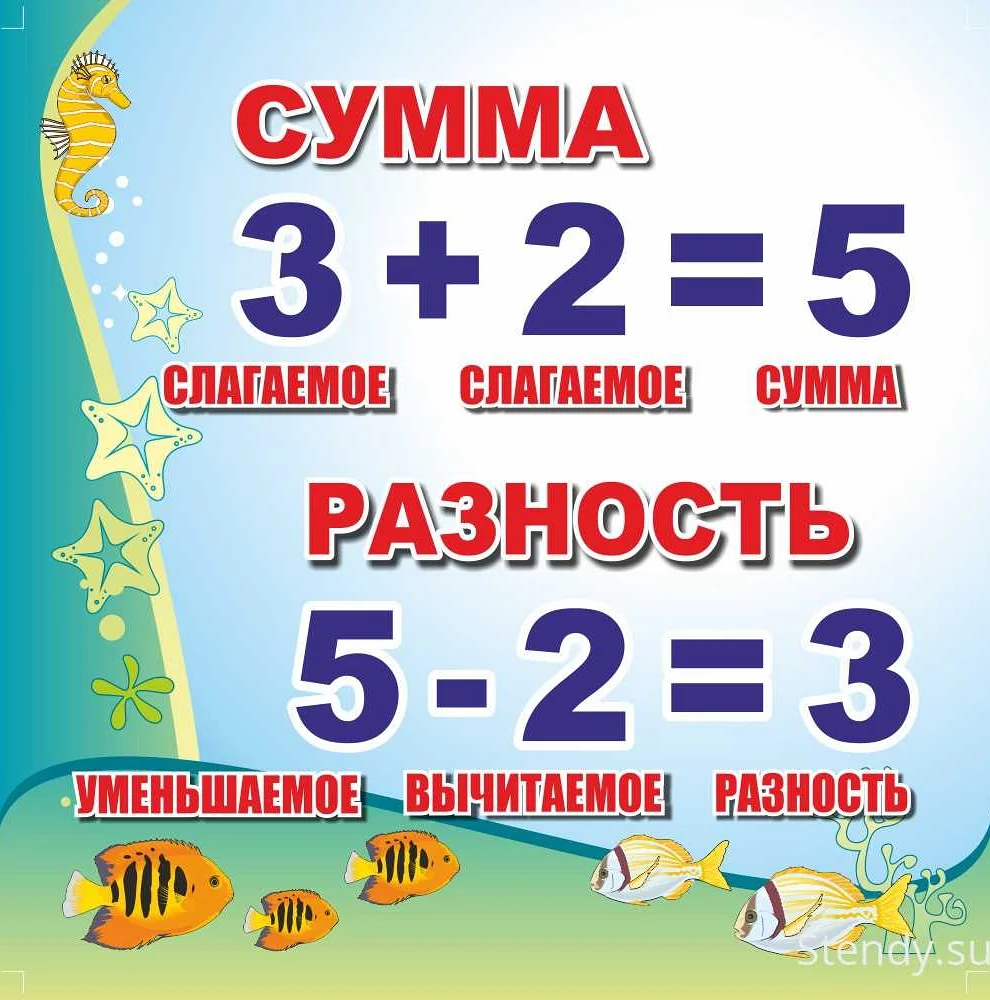
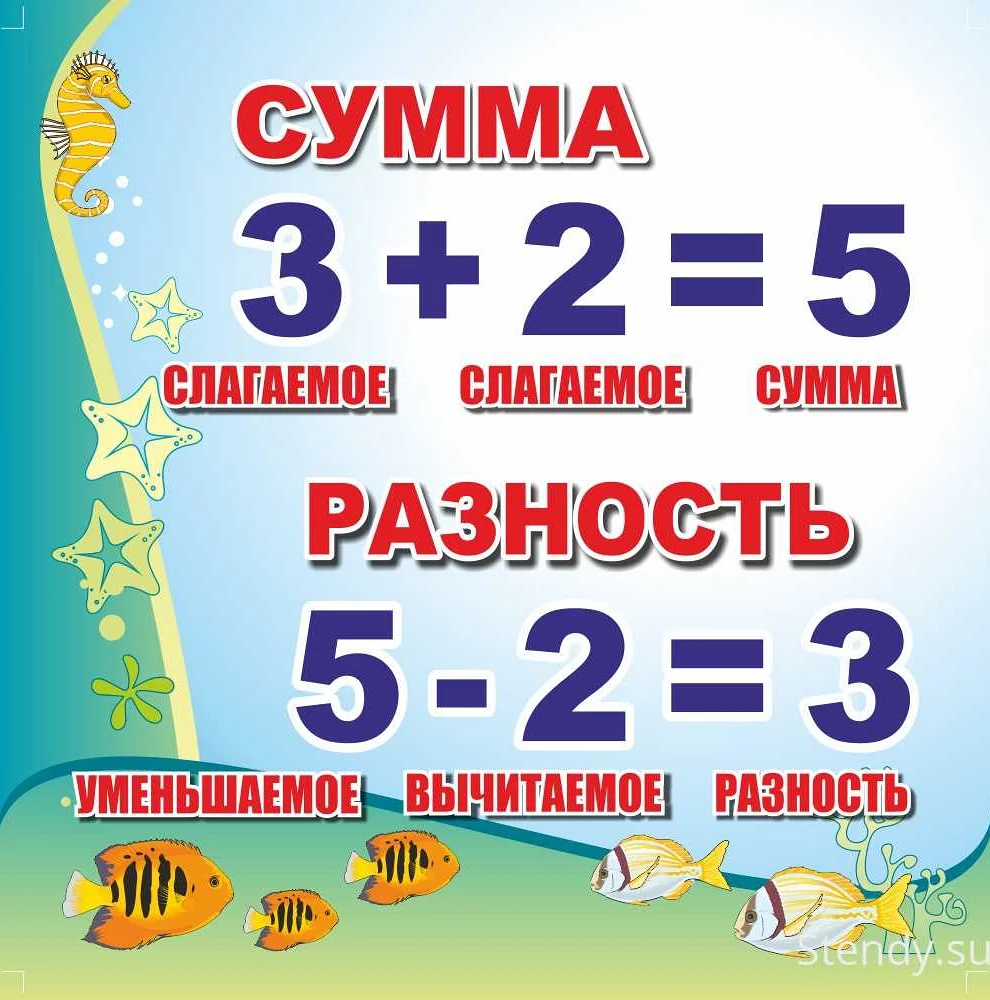
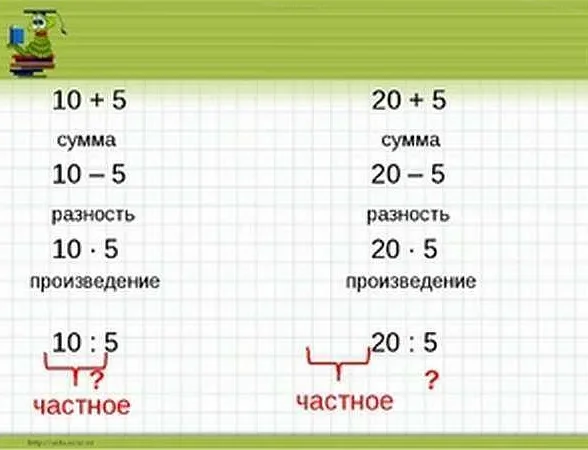
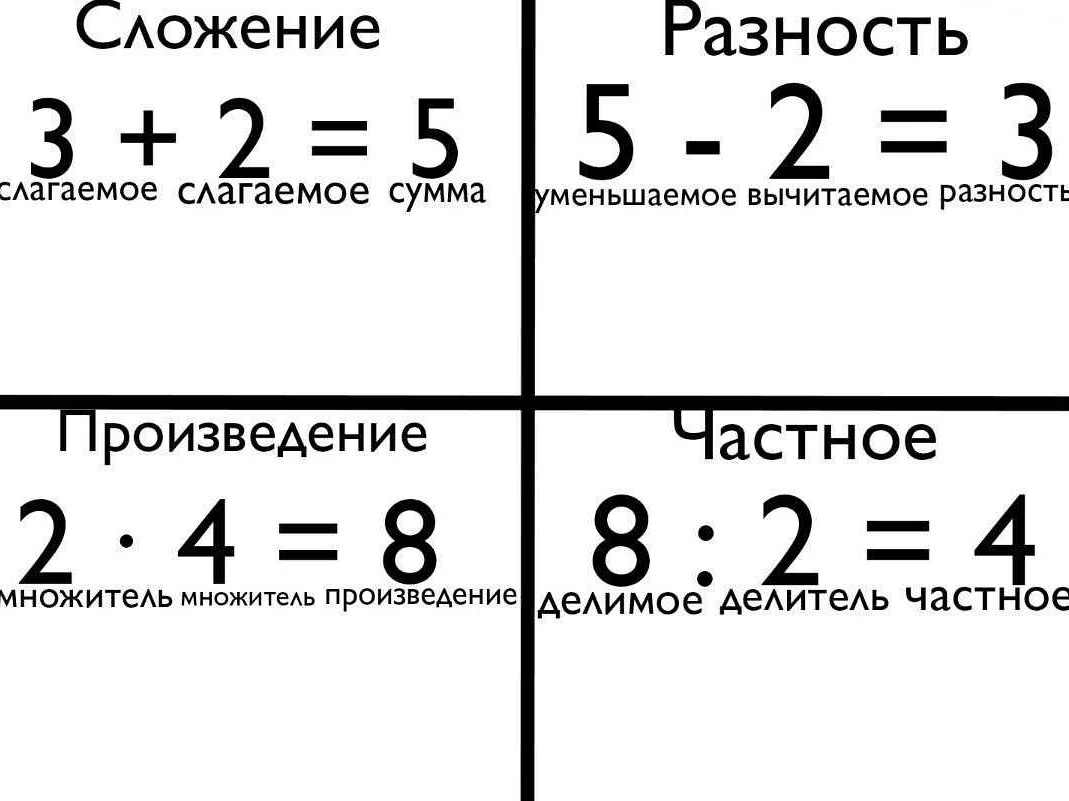
Произведение и частное — это две основные операции в математике. Произведение — это результат умножения двух чисел, а частное — результат деления одного числа на другое. В данной статье мы рассмотрим подробности и особенности этих операций, а также приведем примеры их использования в различных задачах и уравнениях.

Произведение и частное, а также сумма и разность — это базовые операции в математике, которые используются для решения различных задач. Произведение обозначается символом умножения «×», а частное — символом деления «÷». Сумма обозначается символом «+» и используется для нахождения общего результата двух или более чисел. Разность обозначается символом «-» и используется для нахождения разницы между двумя числами.

Каждая из этих операций имеет свои особенности. Произведение двух чисел равно их умножению, то есть результатом является число, которое получается при повторении одного числа столько раз, сколько указано другим числом. Например, произведение чисел 2 и 3 равно 6, так как 2 × 3 = 6.

Частное двух чисел равно их делению, то есть результатом является число, которое получается при разделении одного числа на другое. Например, частное чисел 10 и 2 равно 5, так как 10 ÷ 2 = 5.

Важно отметить, что деление на ноль запрещено в математике, поскольку не имеет смысла разделять что-то на ноль.

Сумма двух чисел равна их сложению, то есть результатом является число, которое получается при объединении двух чисел вместе. Например, сумма чисел 5 и 3 равна 8, так как 5 + 3 = 8.

Разность двух чисел равна их вычитанию, то есть результатом является число, которое получается при вычитании одного числа из другого. Например, разность чисел 7 и 4 равна 3, так как 7 — 4 = 3.

Произведение и частное: определение и суть

Произведение двух чисел — это результат умножения этих чисел. При умножении, первое число называется множимым, а второе — множителем. Произведение вычисляется путем повторения множимого числа столько раз, сколько указано в множителе.

Частное двух чисел — это результат деления одного числа на другое. При делении, первое число называется делимым, а второе — делителем. Частное вычисляется путем определения, сколько раз делитель содержится в делимом. Если деление происходит без остатка, то результатом будет целое число, если с остатком — десятичная дробь.

Произведение и частное являются взаимообратными операциями: произведение двух чисел может быть получено путем многократного сложения одного из этих чисел, а частное может быть получено путем многократного вычитания делителя из делимого.

Важно отметить, что при умножении и делении чисел возможно изменение порядка следования сомножителей и делимых без изменения результата. Также, при умножении и делении можно использовать ассоциативность и коммутативность операций для более удобного вычисления.

Видео по теме:

Математическое понятие произведения

Произведение чисел имеет свои особенности. Если умножить число на 1, то результат будет равен исходному числу. Например, 5 × 1 = 5.

Если умножить число на 0, то результат всегда будет равен 0. Например, 7 × 0 = 0.

Если умножить число на -1, то результат будет числом с противоположным знаком. Например, 4 × (-1) = -4.

Произведение двух чисел может быть больше или меньше исходных чисел, в зависимости от их знаков и величин. Например, 3 × 2 = 6, а 3 × (-2) = -6.

Для умножения чисел используются таблицы умножения и различные алгоритмы, такие как «столбиковое умножение» или «каррирование».

Произведение является одной из основных операций в математике и широко используется в различных областях, включая физику, экономику и программирование.

Роль произведения в математике

В арифметике произведение двух чисел можно представить как сумму этого числа, взятое сколько-то раз. Например, произведение 3 и 4 равно 12, что означает, что число 3 было взято 4 раза и сложено. Это позволяет нам умножать числа любой величины и получать их произведение.

Произведение также используется в алгебре для выражения отношения между переменными. Например, выражение 2x означает, что переменная x умножена на 2. Произведение переменных может помочь нам моделировать реальные ситуации и решать сложные задачи.

Особенностью произведения является коммутативность, то есть порядок перемножаемых чисел не влияет на результат. Например, произведение 2 и 3 равно 6, а произведение 3 и 2 также равно 6. Это свойство позволяет нам удобно выполнять вычисления и упрощать математические выражения.

Кроме того, произведение имеет связь с другими операциями, такими как сумма и разность. Например, если мы знаем сумму двух чисел и одно из них, то мы можем найти другое число с помощью деления. Также, при решении уравнений и систем уравнений произведение может помочь нам найти значения переменных.

В заключение, произведение играет важную роль в математике, позволяя нам умножать числа, выражать отношения между переменными, решать задачи и упрощать вычисления. Знание и понимание произведения помогает развить навыки математического мышления и применять их в реальной жизни.

Вопрос-ответ:

Какое понятие лежит в основе операций в математике?

Основой операций в математике является понятие произведения и частного, которые определяются как результат умножения и деления соответственно.

Какими особенностями обладают произведение и частное в математике?

Произведение и частное обладают рядом особенностей: коммутативностью, ассоциативностью, дистрибутивностью и нейтральным элементом.

Какие свойства имеют операции сложения и вычитания в математике?

Сложение и вычитание обладают свойствами коммутативности и ассоциативности, приоритетом сложения перед вычитанием и наличием нейтральных элементов.

Какие различия между произведением и частным можно выделить?

Основное различие между произведением и частным заключается в том, что произведение получается умножением двух или более чисел, а частное — делением одного числа на другое.

Особенности произведения

Одной из особенностей произведения является то, что порядок сомножителей не влияет на результат. То есть, произведение двух чисел будет одинаковым независимо от того, какое из чисел будет стоять первым, а какое – вторым. Например, произведение чисел 3 и 4 равно 12, а произведение чисел 4 и 3 также равно 12.

Еще одной особенностью произведения является то, что если один из сомножителей равен нулю, то произведение всегда будет равно нулю. Например, произведение чисел 0 и 7 равно 0, а произведение чисел 9 и 0 также равно 0. Это свойство произведения можно использовать для решения задач, которые связаны с нахождением нулевого значения.

Также стоит отметить, что произведение любого числа на единицу всегда равно этому числу. Например, произведение числа 5 и 1 равно 5, а произведение числа 10 и 1 также равно 10. Это свойство произведения помогает упрощать вычисления и делает его более удобным в использовании.

И наконец, произведение любого числа на -1 всегда будет отрицательным числом. Например, произведение числа 8 и -1 равно -8, а произведение числа -3 и -1 равно 3. Это свойство произведения тесно связано со знаками чисел и является одним из ключевых при выполнении операций с отрицательными числами.

Математическое понятие частного

Частное двух чисел можно вычислить, разделив делимое на делитель. Если делимое является большим числом, то частное будет положительным. Если делимое отрицательное, а делитель положительный, то частное будет отрицательным. Если оба числа отрицательные, то частное будет положительным.

Частное имеет свои особенности. Например, деление на ноль невозможно. Если делитель равен нулю, то частное неопределено (обозначается как «∞»).

Кроме того, частное может быть представлено в виде десятичной дроби или числа с плавающей точкой. В этом случае, число после запятой указывает на точность вычисления.

В математике, частное является важным понятием и используется в различных областях, таких как алгебра, геометрия, физика и экономика. Понимание понятия частного позволяет проводить различные вычисления и решать задачи, связанные с делением чисел.

Значение частного в математике

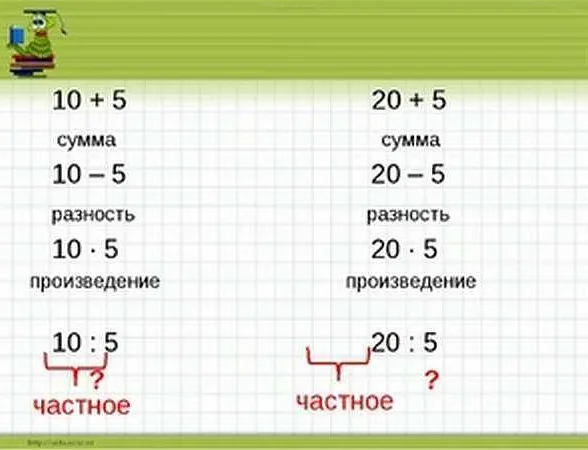
Значение частного позволяет определить, сколько раз одно число содержится в другом числе. Если результат деления двух чисел является целым числом, то это означает, что одно число содержится в другом число целое количество раз.

Для вычисления частного используется символ деления «/», который разделяет делимое и делитель. Например, если мы хотим найти частное чисел 10 и 2, запись будет выглядеть следующим образом: 10 / 2.

Частное может быть как целым числом, так и десятичной дробью. В случае десятичной дроби, она может быть ограничена определенным количеством знаков после запятой или представлена в виде бесконечной десятичной дроби.

Частное также можно представить в виде произведения делимого и обратной величины делителя. Например, частное чисел 10 и 2 можно представить как 10 * (1/2) = 5.

ДелимоеДелительЧастное

10

2

5

Значение частного имеет важное значение во многих областях математики, а также в реальном мире. Например, оно используется для расчетов в экономике, физике, статистике и других науках.

Особенности частного

Первая особенность частного заключается в том, что если делитель равен нулю, то на ноль делить нельзя. Это связано с тем, что деление на ноль является недопустимой операцией в математике. Поэтому, при делении на ноль частное не определено.

Вторая особенность связана с тем, что результатом деления является рациональное число, то есть число, которое может быть представлено в виде дроби, где числитель и знаменатель являются целыми числами без остатка. Например, при делении числа 10 на число 3 результатом будет десятичная дробь 3.333…, которая может быть представлена в виде обыкновенной дроби 10/3.

Третья особенность связана с тем, что при делении числа на себя результат всегда будет равен 1. Например, любое число, деленное на себя, например, 5 / 5, даст результат 1.

Четвертая особенность заключается в том, что при делении числа на единицу результат всегда будет равен этому числу. Например, любое число, деленное на единицу, например, 7 / 1, даст результат 7.

Пятая особенность заключается в том, что при делении нуля на любое число результат всегда будет равен нулю. Например, 0 / 5 = 0.

Важно помнить, что при выполнении деления нужно учитывать эти особенности, чтобы правильно определить результат операции и избежать ошибок.

Разность и сумма: связь с произведением и частным

Произведение и частное, в свою очередь, также имеют тесную связь с разностью и суммой. Произведение двух чисел является результатом умножения этих чисел, а частное — результатом деления одного числа на другое.

Связь между разностью и произведением заключается в том, что их результатами являются числа, которые могут быть получены из других чисел. Например, если у нас есть два числа a и b, то разность a — b может быть представлена как произведение a на -1, умноженное на b.

Связь между суммой и произведением состоит в том, что сумма двух чисел может быть представлена как произведение одного из этих чисел на 1, плюс другое число. Например, сумма a + b может быть представлена как произведение a на 1, плюс b.

Произведение и частное также могут быть выражены с использованием разности и суммы. Например, произведение a и b может быть представлено как сумма a + a + … + a (b раз), а частное двух чисел может быть представлено как разность между этими числами, деленная на 1.

ОперацияСвязь с разностью и суммойСвязь с произведением и частным

Разность	Обратная операция к сумме	Может быть выражена через произведение
Сумма	Обратная операция к разности	Может быть выражена через произведение
Произведение	Может быть выражено через разность и сумму	Может быть выражено через разность и сумму
Частное	Может быть выражено через разность и сумму	Может быть выражено через разность и сумму