Что такое свойство в математике определение

Свойство в математике — это характеристика или качество, присущее определенному объекту или явлению. Оно позволяет установить отношения между элементами и решать различные задачи. Понимание свойств математических объектов является основой для развития математической науки и ее применения в различных областях. В данной статье рассматривается определение и примеры свойств в математике.

Свойство — это особенность, характеристика объекта или явления, которая позволяет выделить его из множества других объектов или явлений. В математике свойство определяется как утверждение, которое истинно для всех элементов некоторого множества.

Основная задача свойств в математике заключается в классификации объектов и установлении особенностей, которые позволяют выделить их из общей массы. Свойства могут быть как общими, присущими всем объектам некоторого множества, так и специфическими, характерными только для определенных объектов.

Примером свойства в математике может служить коммутативность операции сложения чисел. Это свойство гласит, что результат сложения двух чисел не зависит от порядка, в котором производится сложение. Например, для любых чисел a и b выполняется равенство a + b = b + a. Таким образом, коммутативность является характеристикой операции сложения и позволяет классифицировать ее как свойство, присущее всем числам.

Свойства в математике играют важную роль в построении логического рассуждения и вывода. Они позволяют упрощать вычисления, обобщать результаты и строить новые математические теории. Понимание свойств и их правильное применение помогает ученикам и специалистам в области математики более полно и глубоко понять и использовать различные концепции и методы этой науки.

Свойство в математике: определение и примеры

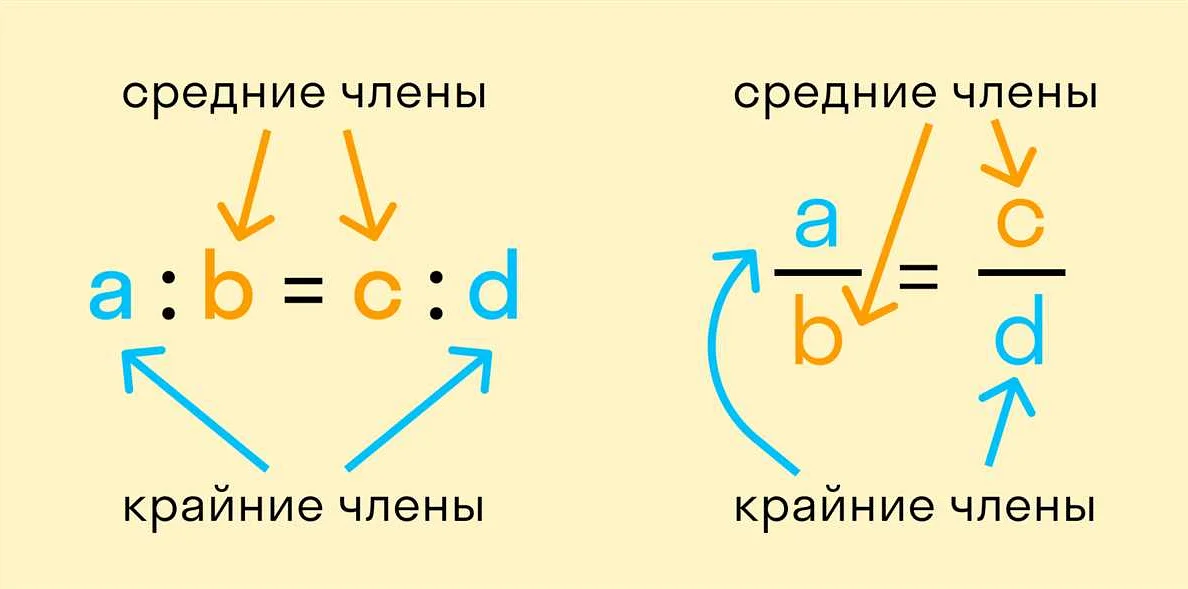
Существует множество различных свойств в математике, которые могут быть применены к различным математическим объектам. Некоторые из наиболее известных свойств в математике включают:

Свойство	Описание	Пример
Коммутативность	Операция может быть выполнена в любом порядке	1 + 2 = 2 + 1
Ассоциативность	Порядок операций не влияет на результат	(1 + 2) + 3 = 1 + (2 + 3)
Дистрибутивность	Операция распространяется на сумму или разность	2 * (3 + 4) = (2 * 3) + (2 * 4)
Идемпотентность	Повторение операции не меняет результат	1 + 1 = 1
Инверсия	Существует обратный элемент для операции	2 + (-2) = 0

Это лишь некоторые из множества свойств, которые могут быть применены в математике. Знание и понимание свойств помогают упростить и анализировать математические выражения, а также сформулировать и доказать теоремы и утверждения.

Понятие свойства в математике

Свойства могут быть качественными или количественными. Качественные свойства описывают качество или признак объекта. Например, цвет, форма, размер и т.д. Количественные свойства, в свою очередь, выражаются числовыми значениями. Например, длина, масса, объем и т.д.

Примеры свойств в математике могут быть следующими:

• Число 4 является четным.
• Треугольник ABC является равносторонним.
• Множество A содержит только положительные числа.
• Функция f(x) является непрерывной на интервале (a, b).

Свойства играют важную роль в математике, так как они позволяют анализировать и классифицировать объекты и явления, а также строить логические доказательства.

Основные характеристики свойств в математике

Свойства в математике обладают несколькими основными характеристиками, которые помогают установить их определение и принципы работы.

1. Идентичность: свойство идентичности означает, что объекты, которые им обладают, остаются неизменными при определенных операциях. Например, в арифметике свойство идентичности выражается через ноль и единицу: при сложении нуля с любым числом или умножении числа на единицу результат остается неизменным.

2. Ассоциативность: свойство ассоциативности говорит о том, что результат операции не зависит от порядка ее выполнения. Например, в арифметике свойство ассоциативности выражается через скобки: (а + b) + c = а + (b + c).

3. Коммутативность: свойство коммутативности позволяет менять порядок операндов без изменения результата. Например, в арифметике свойство коммутативности выражается через сложение и умножение: а + b = b + а, а * b = b * а.

4. Дистрибутивность: свойство дистрибутивности определяет связь между двумя операциями. Например, в арифметике свойство дистрибутивности выражается через умножение и сложение: а * (b + c) = а * b + а * c.

5. Обратимость: свойство обратимости говорит о том, что существует обратная операция, которая отменяет действие данной операции. Например, в арифметике свойство обратимости выражается через сложение и вычитание: а + (-а) = 0.

6. Закон нейтрального элемента: свойство нейтрального элемента позволяет выполнять операцию с особым элементом, который не изменяет результат. Например, в арифметике ноль является нейтральным элементом для сложения: а + 0 = а.

Эти основные характеристики свойств в математике позволяют нам лучше понять и работать с различными математическими концепциями и операциями.

Примеры свойств в математике

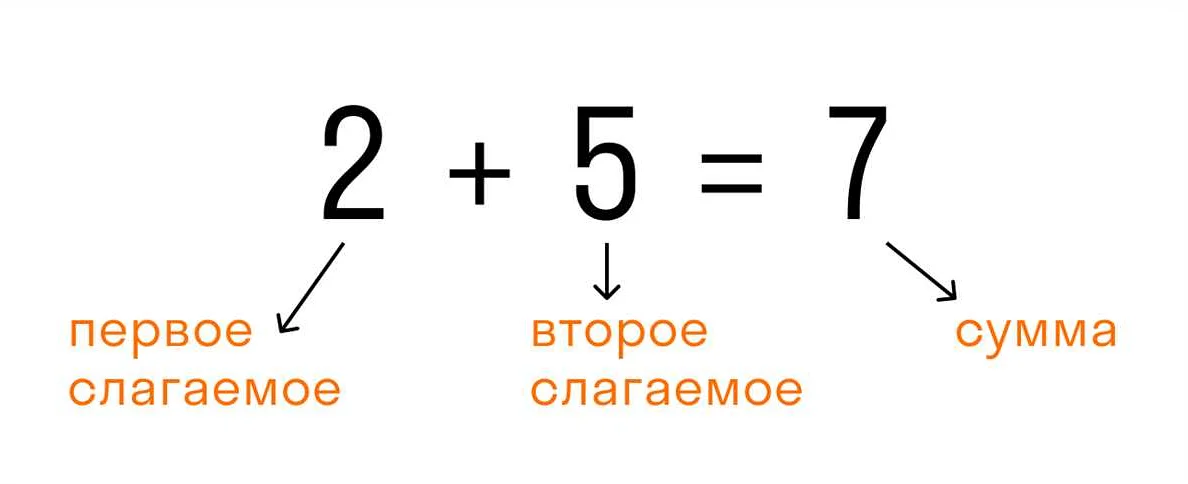
1. Коммутативное свойство сложения и умножения:

Свойство коммутативности означает, что порядок слагаемых или множителей не влияет на результат операции. Например, для любых чисел а и b выполняется:

а + b = b + a

а * b = b * a

2. Ассоциативное свойство сложения и умножения:

Свойство ассоциативности позволяет менять местами скобки при выполнении операции сложения или умножения трех или более чисел. Например, для любых чисел а, b и с выполняется:

(а + b) + с = а + (b + с)

(а * b) * с = а * (b * с)

3. Дистрибутивное свойство умножения относительно сложения:

Свойство дистрибутивности позволяет раскрывать скобки при выполнении операции умножения и сложения. Например, для любых чисел а, b и с выполняется:

а * (b + с) = а * b + а * с

4. Свойство нейтрального элемента сложения и умножения:

Свойство нейтрального элемента означает, что существуют такие числа, которые не меняют результат при сложении или умножении. Например, для любого числа а выполняется:

а + 0 = а

а * 1 = а

5. Свойство обратного элемента сложения и умножения:

Свойство обратного элемента означает, что для каждого числа существует такое число, которое при сложении или умножении с ним дает нейтральный элемент. Например, для любого числа а существует число -а, такое что выполняется:

а + (-а) = 0

а * (1/а) = 1

Классификация свойств в математике

Свойства в математике могут быть разделены на несколько классов в зависимости от их характеристик и способа применения. Рассмотрим основные классификации свойств:

1. Операционные свойства. Эти свойства определяют, как изменяются объекты или операции при выполнении определенных операций. Примерами операционных свойств могут служить коммутативность, ассоциативность и дистрибутивность операций.
2. Структурные свойства. Эти свойства характеризуют определенные структуры, такие как множества, группы, поля и т.д. Примерами структурных свойств могут служить замкнутость, абелевость и единица.
3. Сравнительные свойства. Эти свойства позволяют сравнивать объекты или операции и устанавливать их отношения. Примерами сравнительных свойств могут служить упорядоченность, эквивалентность и мощность.
4. Алгебраические свойства. Эти свойства относятся к алгебре и описывают специфические характеристики операций и объектов. Примерами алгебраических свойств могут служить ассоциативность, коммутативность и существование обратного элемента.
5. Геометрические свойства. Эти свойства относятся к геометрии и описывают особенности геометрических объектов и отношений между ними. Примерами геометрических свойств могут служить симметрия, параллельность и перпендикулярность.

Классификация свойств в математике позволяет упорядочить и систематизировать знания о различных характеристиках объектов и операций. Это помогает математикам анализировать, описывать и решать различные задачи, основываясь на свойствах их элементов.

Важность свойств в математических доказательствах

Одним из ключевых свойств, используемых в математических доказательствах, является свойство транзитивности. Оно гласит, что если элемент А связан с элементом В, а элемент В связан с элементом С, то элемент А также связан с элементом С. Это свойство позволяет устанавливать логические связи и делать выводы на основе уже установленных отношений.

Другим важным свойством является свойство симметрии. Оно гласит, что если элемент А связан с элементом В, то элемент В также связан с элементом А. Симметричность позволяет устанавливать взаимные связи и делать обратные выводы.

Свойства также могут быть использованы для установления эквивалентности или неравенства между математическими объектами. Например, свойство рефлексивности позволяет установить эквивалентность объекта с самим собой, а свойство ассоциативности позволяет менять порядок операций без изменения результата.

Все эти свойства, а также множество других, являются основой для строительства математических доказательств. Они позволяют устанавливать логические связи между объектами, выводить новые утверждения и формализовать математические концепции. Без использования свойств математические доказательства были бы гораздо менее эффективными и затруднительными.

Видео по теме:

Вопрос-ответ:

Что такое свойство в математике?

Свойство в математике — это характеристика, которую можно присвоить объекту или группе объектов. Оно может быть истинным или ложным для каждого объекта в группе. Например, «быть четным числом» — это свойство, которое истинно для чисел 2, 4, 6 и т.д., но ложно для чисел 1, 3, 5 и т.д.

Какие бывают примеры свойств в математике?

В математике существует множество примеров свойств. Некоторые из них могут быть достаточно простыми, например, «быть положительным числом» или «иметь длину больше 5». Другие могут быть более сложными, например, «быть простым числом» или «быть выпуклым многоугольником». Каждое свойство определяется в зависимости от контекста или области математики, в которой оно используется.

Как можно определить свойство в математике?

Свойство в математике можно определить с помощью логических высказываний. Например, для свойства «быть четным числом» можно сформулировать следующее логическое высказывание: «Если число делится на 2 без остатка, то оно является четным числом». Таким образом, определение свойства в математике сводится к установлению условий, при которых оно является истинным для объектов или группы объектов.

Можно ли свойства в математике классифицировать?

Да, свойства в математике можно классифицировать по различным признакам. Одно из возможных делений — на алгебраические и топологические свойства. Алгебраические свойства зависят от операций, определенных на объектах, например, свойство «быть коммутативным» или «быть ассоциативным». Топологические свойства относятся к геометрическим свойствам объектов, например, свойство «быть выпуклым» или «быть связным». В рамках каждой из этих категорий свойства могут быть дополнительно классифицированы.

Зачем нужно изучать свойства в математике?

Изучение свойств в математике позволяет установить общие закономерности и правила, которые применимы к различным объектам или группам объектов. Оно помогает понять, какие условия должны быть выполнены для того, чтобы объект обладал определенным свойством. Это важно для доказательства теорем, развития новых математических методов и приложений в различных областях, таких как физика, экономика, компьютерная наука и др.

Взаимосвязь свойств в математике

Свойства в математике часто взаимосвязаны и могут быть использованы вместе для решения различных задач. Рассмотрим некоторые примеры такой взаимосвязи.

СвойствоПример связи

Коммутативность сложения	Если a + b = c, то b + a = c.
Ассоциативность умножения	Если (a * b) * c = d, то a * (b * c) = d.
Распределительное свойство	Если a * (b + c) = d, то a * b + a * c = d.
Свойство нуля	Если a + 0 = a, то 0 + a = a.
Свойство единицы	Если a * 1 = a, то 1 * a = a.

Это лишь некоторые примеры взаимосвязи свойств в математике. Понимание этих взаимосвязей помогает упрощать вычисления и решать математические задачи более эффективно.

Практическое применение свойств в математике

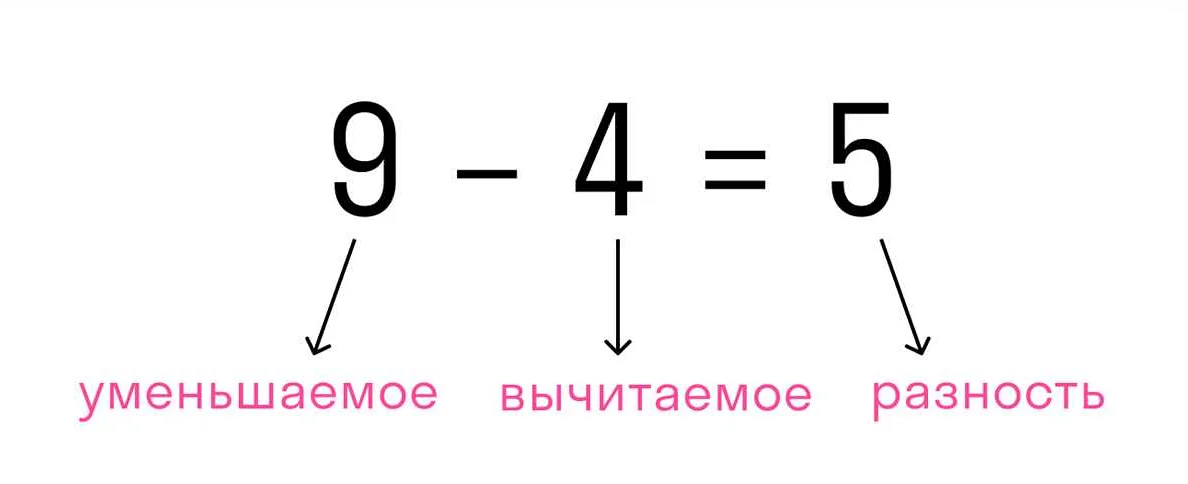
Свойства в математике имеют большое практическое значение и широко применяются в различных областях науки, техники и повседневной жизни. Вот несколько примеров:

Свойство коммутативности сложения: Это свойство позволяет менять порядок слагаемых без изменения результата. Например, если мы имеем два числа a и b, то a + b будет равно b + a. Это свойство используется во многих практических ситуациях, например, при суммировании чисел или при перестановке слагаемых в алгебраических выражениях.	Свойство дистрибутивности умножения относительно сложения: Это свойство позволяет распределить умножение на сумму двух чисел. Например, если мы имеем три числа a, b и c, то a * (b + c) будет равно a * b + a * c. Это свойство используется, например, при раскрытии скобок в алгебраических выражениях или при вычислении площади прямоугольника.
Свойство ассоциативности умножения: Это свойство позволяет менять порядок множителей без изменения результата. Например, если у нас есть три числа a, b и c, то (a * b) * c будет равно a * (b * c). Это свойство используется, например, при упрощении алгебраических выражений или при перемножении матриц.	Свойство нулевого элемента сложения: Это свойство гласит, что сумма числа и нуля равна этому числу. Например, a + 0 будет равно a. Это свойство используется во многих задачах, например, при вычитании чисел или при решении уравнений.

Это только некоторые примеры применения свойств в математике. Свойства помогают упрощать вычисления, делать операции более эффективными и удобными, а также открывают новые возможности для исследования и решения различных задач.