Что такое точка в математике

Точка в математике — это элементарное понятие, обозначающее местоположение в пространстве без размеров. Она характеризуется своими координатами и может быть использована для построения линий, графиков и других математических объектов.

В математике точка — это одномерный объект, который не имеет ни размера, ни формы. Она представляет собой абстрактную концентрацию. Точка в математике является базовым понятием и используется для описания и изучения пространства, а также других математических объектов и явлений.

Точка характеризуется своими координатами, которые определяют ее положение в пространстве. Координаты точки могут быть заданы в различных системах координат, таких как декартовая, полярная или сферическая. Координаты точки могут быть числами, векторами или другими математическими объектами.

Точка обладает несколькими свойствами, которые определяют ее особенности и взаимодействие с другими объектами. Одно из основных свойств точки — ее неподвижность. Точка не может перемещаться или изменять свое положение без внешнего воздействия. Она также не имеет направления или ориентации.

В математике точка широко используется для решения различных задач и задачей в различных областях. Она является основой для построения геометрических фигур, линий и поверхностей. Точки также используются в анализе и алгебре для описания функций, их графиков и решения уравнений. Точки также играют важную роль в физике, географии, экономике и других науках, где они помогают в описании и анализе различных явлений и процессов.

Определение точки в математике

Обозначается точка обычно прописной буквой латинского алфавита, например, точка A, B, C и так далее. Кроме того, точку можно задать координатами на плоскости или в пространстве.

Точка является основным строительным элементом в геометрии и используется для построения линий, отрезков, углов и других геометрических фигур. Она также является основой для определения расстояния между двумя точками и других важных понятий в математике.

Примечание: В математике точка может иметь и другие определения в зависимости от области применения, например, в теории множеств, анализе и др.

Свойства точки в математике

• Точка не имеет ни размеров, ни формы. Она считается объектом безразмерным.
• Точка может быть определена только посредством ее координат или относительного положения относительно других точек.
• Точка может находиться в пространстве, на плоскости или на прямой.
• Точка может быть задана с помощью своих координат в системе координат.
• Точка может быть неподвижной или перемещаться в пространстве.
• Точка может быть отображена на графике или в координатной системе.
• Точка может быть началом или концом отрезка, луча или прямой.
• Точка может быть точкой пересечения двух или более объектов.

Свойства точки в математике позволяют разрабатывать различные теории и модели, а также применять математические методы в различных областях науки и техники, таких как физика, инженерия, компьютерная графика и др.

Применение точки в математике

Применение точек в математике наиболее ярко проявляется в геометрии. В геометрии точки используются для обозначения положения и расстояния между объектами. Точки могут быть использованы для построения прямых, плоскостей, графиков функций и других геометрических фигур.

Точки также играют важную роль в анализе и алгебре. В анализе точки используются для определения пределов, производных и интегралов функций. В алгебре точки могут представлять значения переменных и использоваться для построения графиков и решения уравнений.

Во многих других областях математики, таких как теория вероятностей, математическая статистика и математическая физика, точки используются для описания вероятностных распределений, статистических данных и физических объектов.

Точки также имеют важное значение в компьютерной графике и компьютерной алгебре. В компьютерной графике точки используются для представления и отображения геометрических объектов на экране. В компьютерной алгебре точки могут быть использованы для выполнения различных математических операций, таких как сложение, вычитание, умножение и деление.

В заключение, точка является фундаментальным понятием в математике и имеет широкое применение в различных областях. Без использования точек, многие математические концепции и методы были бы невозможны.

Точка как элементарная геометрическая фигура

Точка в геометрии используется для определения положения объектов в пространстве. Она не имеет длины, ширины и высоты, и может быть представлена как абстрактный объект без каких-либо конкретных характеристик. Точка может быть задана координатами в системе координат, которые определяют ее положение относительно других точек.

Точки используются для создания других геометрических фигур, таких как линии, отрезки, отрезки и полигоны. Они также играют важную роль в определении различных геометрических свойств и нахождении решений в задачах геометрии.

Точка в координатной плоскости

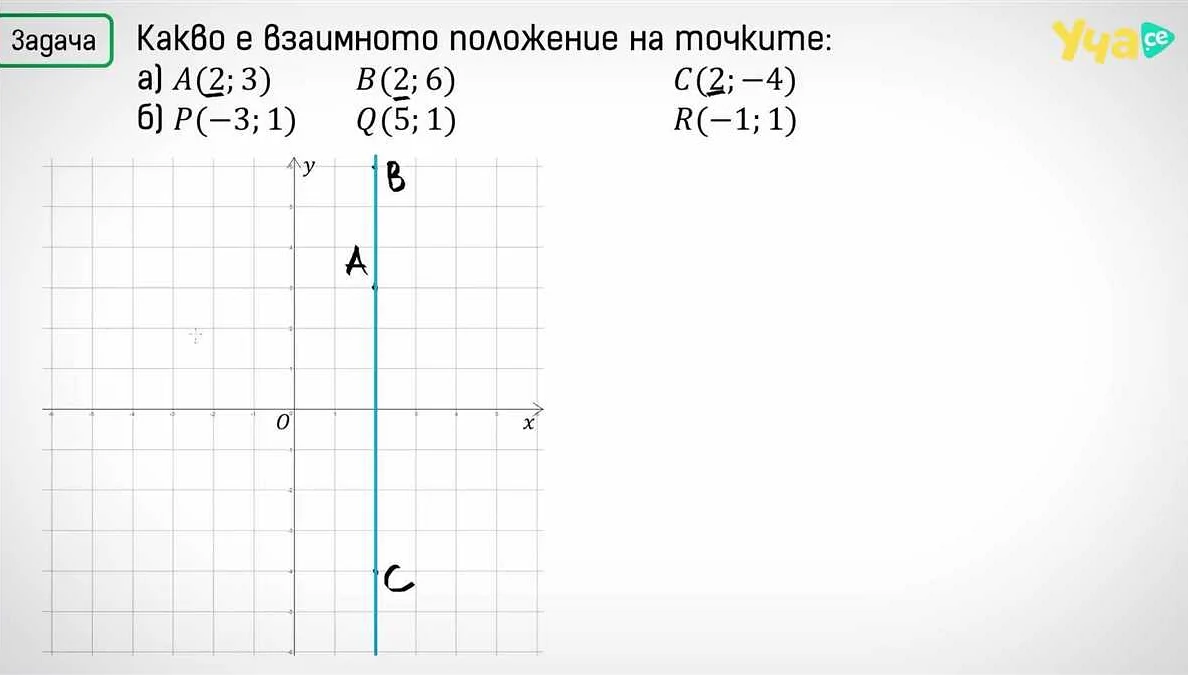
Координатная плоскость представляет собой плоскость, на которой размещены оси координат. Ось x называется горизонтальной, а ось y — вертикальной. Точка на плоскости задается парой чисел (x, y), где x — это расстояние от точки до оси y, а y — расстояние от точки до оси x.

Координатные оси пересекаются в начале координат, которая имеет координаты (0, 0). Таким образом, точка (0, 0) обозначает начало координатной плоскости.

С помощью координат точек можно задавать положение объектов, проводить геометрические построения и решать различные задачи в математике и физике. Например, с помощью точек можно определить расстояние между двумя объектами, провести прямую через две точки, найти координаты точек пересечения графиков функций и многое другое.

Видео по теме:

Вопрос-ответ:

Как можно определить точку в математике?

Точка в математике — это элементарный объект, который не имеет размеров и не имеет никаких других характеристик, кроме своих координат.

Какие свойства есть у точки в математике?

Точка в математике не имеет размеров, она не может быть разделена на части и не имеет никакой внутренней структуры. Она также не имеет направления и не имеет ориентации.

Как точка используется в математике?

Точка в математике используется для задания положения объекта или для определения отношений между объектами. Она также является основным строительным блоком для построения геометрических фигур и решения различных задач.

Какая роль у точки в геометрии?

В геометрии точка является базовым понятием и используется для определения линий, плоскостей и других геометрических фигур. Точка также используется для определения расстояния между объектами и для построения графиков функций.

Можно ли двигать точку в математике?

В математике точка считается неподвижной и не может быть перемещена. Однако, в некоторых случаях можно рассматривать точку как перемещающийся объект и изучать её движение в пространстве.

Что такое точка в математике?

Точка в математике — это одномерный объект, который не имеет ни размеров, ни формы. Она считается базовым элементом геометрии и может быть представлена как маленькая отметка на плоскости или в пространстве.

Какие свойства имеет точка в математике?

Точка в математике обладает несколькими важными свойствами. Она не имеет ни длины, ни ширины, ни толщины, и ее положение полностью определяется координатами на плоскости или в пространстве. Кроме того, точка не может быть разделена или разложена на составные части.

Абстрактная точка и ее свойства

Одним из таких определений является абстрактная точка. Абстрактная точка представляет собой идеализированное математическое понятие, которое не имеет никаких размеров и не обладает никакими другими свойствами.

Основное свойство абстрактной точки заключается в том, что она может быть использована в качестве начальной точки для построения различных геометрических фигур и объектов. Например, с помощью абстрактной точки можно построить линию, плоскость, окружность и другие геометрические объекты.

Абстрактная точка не имеет никаких ориентаций и направлений. Она может быть перемещена в любую точку пространства без изменения своих свойств. Также абстрактная точка не имеет никакого размера и формы, она существует только как математическое понятие.

Важно отметить, что абстрактная точка существует только в математическом пространстве и не имеет аналога в реальном мире. Она используется в математических вычислениях и моделях для упрощения и облегчения анализа геометрических задач.

Таким образом, абстрактная точка является важным понятием в математике, которое позволяет строить и анализировать геометрические объекты. Она не имеет размеров и формы, но может быть использована для создания различных геометрических фигур и объектов.

Точка как базовый элемент в математических моделях

Точка является базовым элементом в математических моделях и используется для определения других геометрических объектов, таких как прямая, плоскость и тело.

Свойства точки включают ее координаты, которые могут быть заданы в различных системах координат, например, декартовой или полярной системе. Координаты точки позволяют определить ее положение относительно других объектов в пространстве.

Точка также может быть определена в контексте функций и графиков. Например, на координатной плоскости точка может быть представлена как пара чисел (x, y), где x — это абсцисса, а y — это ордината.

Точка играет важную роль в математических моделях, таких как геометрия, анализ и теория вероятностей. Она позволяет строить модели и решать различные задачи, связанные с пространственными и числовыми отношениями.