Какую длину имеет математический маятник период колебаний которого 1 секунда

Математический маятник с периодом колебаний в 1 секунду имеет определенную длину, которую можно вычислить с помощью соответствующей формулы. Узнайте, какую длину должен иметь такой маятник, чтобы его период колебаний составлял ровно 1 секунду.

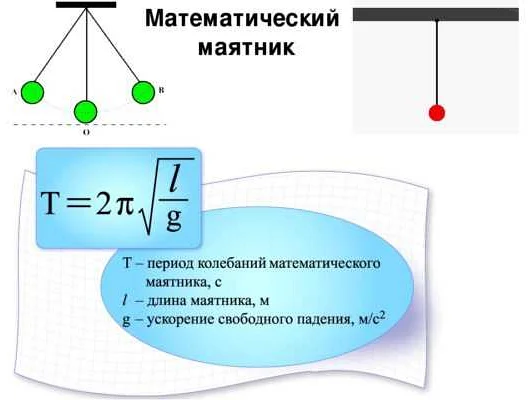
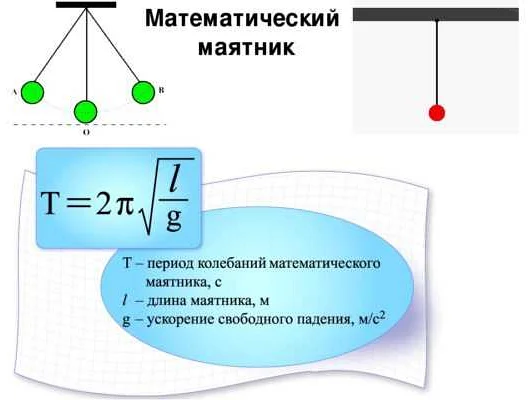
Математический маятник — это физическая система, представляющая собой точечную массу, подвешенную на невесомой нити. Одной из основных характеристик маятника является его период колебаний, который определяет время, за которое маятник совершает полный цикл отклонения и возвращения в исходное положение.

Существует формула, позволяющая вычислить длину математического маятника, при которой период колебаний будет равен 1 секунде. Она основана на известной формуле для периода колебаний маятника и выражается следующим образом:

T = 2π√(L/g)

где T — период колебаний, L — длина маятника и g — ускорение свободного падения.

Из этой формулы следует, что длина математического маятника, при которой его период колебаний будет равен 1 секунде, зависит от ускорения свободного падения. В Международной системе единиц (СИ) ускорение свободного падения принято равным приблизительно 9,81 м/с². Соответственно, для данного значения ускорения свободного падения можно вычислить длину математического маятника, равную:

L = (g/4π²)

Длина математического маятника

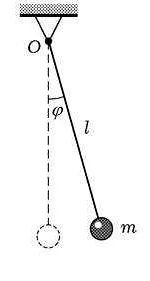
Для математического маятника, длина его подвеса играет важную роль в определении его периода колебаний. Длина маятника измеряется от точки подвеса до центра масс. Чем длиннее маятник, тем больше времени ему требуется для совершения одного полного колебания. Таким образом, длина математического маятника непосредственно влияет на его период колебаний.

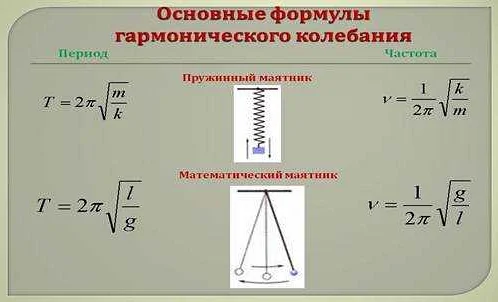
Формула, связывающая длину математического маятника и его период колебаний, называется формулой периода маятника. Она выглядит следующим образом:

Период колебаний (T) = 2π√(l/g),

где l — длина математического маятника, а g — ускорение свободного падения, примерно равное 9,8 м/с² на поверхности Земли.

Уравнение показывает, что период колебаний маятника прямо пропорционален квадратному корню из длины маятника. Таким образом, увеличение длины математического маятника ведет к увеличению его периода колебаний.

Длина математического маятника является одним из фундаментальных параметров в изучении колебаний и волн. Она находит применение в различных областях науки и техники, включая физику, инженерию и архитектуру.

Определение и принцип работы

Принцип работы математического маятника основан на его колебаниях под действием силы тяжести. При отклонении от положения равновесия, маятник начинает колебаться в плоскости его подвеса. Колебания происходят вокруг положения равновесия, которое является точкой, где сила тяжести и сила натяжения нити уравновешивают друг друга.

Период колебаний математического маятника — это время, за которое он совершает одно полное колебание. Длина нити математического маятника влияет на его период колебаний. Согласно формуле периода колебаний математического маятника, период обратно пропорционален квадратному корню из длины нити. То есть, чем длиннее нить, тем больше период колебаний.

Длина нити, мПериод колебаний, с

1	1
2	1.414
3	1.732

Из таблицы видно, что при увеличении длины нити период колебаний математического маятника также увеличивается. Этот принцип используется в различных сферах, включая физику, инженерию, и даже музыку.

Влияние длины на период колебаний

Согласно формуле периода колебаний математического маятника:

T = 2π√(l/g),

где T — период колебаний, l — длина маятника, g — ускорение свободного падения.

Из этой формулы следует, что длина маятника прямо пропорциональна квадратному корню из периода колебаний. То есть, чем длиннее маятник, тем дольше его период колебаний.

Например, если длина математического маятника составляет 1 метр, то его период колебаний будет равен 2π√(1/9.8) ≈ 2.006 секунды.

Таким образом, изменение длины математического маятника позволяет контролировать его период колебаний и использовать его в различных приложениях, таких как измерение времени или создание метронома.

Связь длины и частоты колебаний

Период колебаний – это время, за которое математический маятник совершает одно полное колебание в одну сторону и обратно. Он зависит от длины маятника и ускорения свободного падения, которое на Земле принято равным примерно 9,8 м/с².

Формула, связывающая длину маятника (L) и его период колебаний (T), называется формулой периода колебаний математического маятника:

ФормулаЗначение

T = 2π√(L/g)

где T – период колебаний, L – длина маятника, g – ускорение свободного падения

Из этой формулы видно, что период колебаний математического маятника пропорционален квадратному корню из его длины. То есть, увеличение длины маятника приводит к увеличению его периода колебаний.

Из данной связи между длиной и периодом колебаний математического маятника следует, что у маятников с разной длиной будут разные периоды колебаний. Например, если длина маятника составит 1 метр, его период колебаний будет равен 2π√(1/9,8) ≈ 2,01 секунды.

Таким образом, длина математического маятника имеет прямую связь с его периодом колебаний, и изменение длины маятника может привести к изменению его времени колебаний.

Математическое описание колебаний

Математическое описание колебаний математического маятника с периодом колебаний 1 секунда основано на применении закона Гармонических колебаний. Закон Гармонических колебаний утверждает, что период колебаний зависит от длины маятника и гравитационного ускорения.

Для математического описания колебаний используется уравнение гармонического осциллятора:

T = 2π√(L/g)

где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

В данном случае, если период колебаний равен 1 секунде, то уравнение принимает следующий вид:

1 = 2π√(L/g)

Отсюда можно выразить длину маятника:

L = (g/4π^2)

Таким образом, для математического маятника с периодом колебаний 1 секунда, его длина будет равна (g/4π^2).

Формула для расчета длины маятника

Длина математического маятника с периодом колебаний в 1 секунду может быть рассчитана с помощью следующей формулы:

L = g * T2 / (4 * π2)

где L — длина маятника, g — ускорение свободного падения, T — период колебаний маятника, π — математическая константа, приближенно равная 3.14159.

Таким образом, для маятника с периодом колебаний в 1 секунду, длину можно рассчитать по формуле:

L = g / (4 * π2)

Эта формула может быть полезна для определения длины маятника в различных физических и научных исследованиях, а также в инженерных расчетах.

Примеры расчета длины маятника

Длина математического маятника с периодом колебаний 1 секунда может быть рассчитана с использованием формулы:

Точный расчет:

Для расчета точной длины маятника воспользуемся формулой периода колебаний:

T = 2π√(L/g)

где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

Подставим известные значения в формулу:

1 = 2π√(L/9.8)

Далее, избавимся от корня, возведя обе части уравнения в квадрат:

1 = 4π^2(L/9.8)

Упростим:

1 = (4π^2L)/9.8

Домножим обе части уравнения на 9.8:

9.8 = 4π^2L

Разделим обе части уравнения на 4π^2:

L = 9.8/(4π^2)

Таким образом, точная длина маятника с периодом колебаний 1 секунда составляет примерно 0.248 метра.

Приближенный расчет:

Для приближенного расчета длины маятника можно воспользоваться формулой:

L = gT^2/(4π^2)

где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

Подставим известные значения в формулу:

L = 9.8*(1^2)/(4π^2)

Упростим:

L = 9.8/(4π^2)

Результат приближенного расчета также составляет примерно 0.248 метра.

Обратите внимание, что приближенный расчет длины маятника дает результат, близкий к точному, но может незначительно отличаться.

Вопрос-ответ:

Какова формула для расчета длины математического маятника с периодом колебаний 1 секунда?

Формула для расчета длины математического маятника с периодом колебаний 1 секунда выглядит следующим образом: L = g/(4π²), где L — длина маятника, g — ускорение свободного падения.

Какие еще факторы влияют на период колебаний математического маятника?

Помимо длины маятника, период колебаний математического маятника зависит также от его массы и ускорения свободного падения. Чем больше масса маятника, тем меньше его период, а чем больше ускорение свободного падения, тем больше период.

Как можно определить длину математического маятника с периодом колебаний 1 секунда?

Для определения длины математического маятника с периодом колебаний 1 секунда необходимо воспользоваться формулой L = g/(4π²), где L — искомая длина маятника, g — ускорение свободного падения. Подставляя значения ускорения свободного падения, можно вычислить значение длины маятника.

Как изменится период колебаний математического маятника, если его длина будет увеличена?

Если длина математического маятника будет увеличена, то его период колебаний также увеличится. Это связано с тем, что период колебаний зависит от длины маятника. Чем длиннее маятник, тем больше времени требуется на одно полное колебание.

Применение в научных и технических задачах

Математическое маятник представляет собой простую модель, которая находит применение во множестве научных и технических задач. Его длина и период колебаний могут быть использованы для решения различных задач, связанных с изучением и предсказанием движения.

Одной из основных областей применения математического маятника является физика. С его помощью можно изучать законы гравитации и движение тел под действием силы тяжести. Математический маятник позволяет проводить эксперименты и получать данные, которые могут быть использованы для проверки теоретических моделей и формулирования новых законов.

Еще одной областью применения математического маятника является инженерия. Он может быть использован для расчета и проектирования механизмов, основанных на принципе колебаний. Например, математический маятник может быть использован для определения оптимальной длины подвеса для маятниковых часов или для расчета параметров подвесной системы моста.

Также математический маятник находит применение в астрономии и геодезии. Он может быть использован для измерения силы тяжести и определения гравитационной постоянной на разных планетах. Кроме того, математический маятник может быть использован для измерения высоты горных вершин и глубины океанов.

Применение математического маятника в научных и технических задачах позволяет получать точные и надежные результаты. Его простота и универсальность делают его важным инструментом для исследований и разработок в различных областях науки и техники.

Видео по теме: