Какую длину имеет математический маятник с периодом колебаний 2 с

Математический маятник с периодом колебаний 2 с имеет определенную длину, которая можно вычислить. Узнайте, какая это длина и как она связана с периодом колебаний маятника.

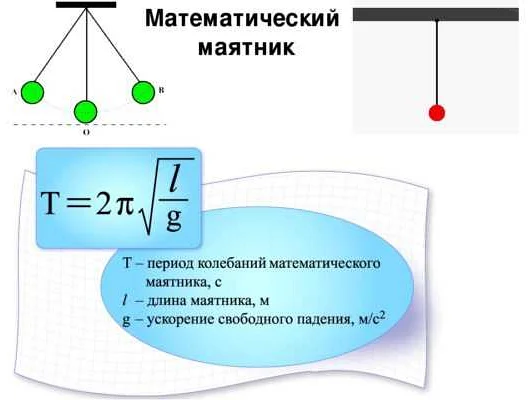
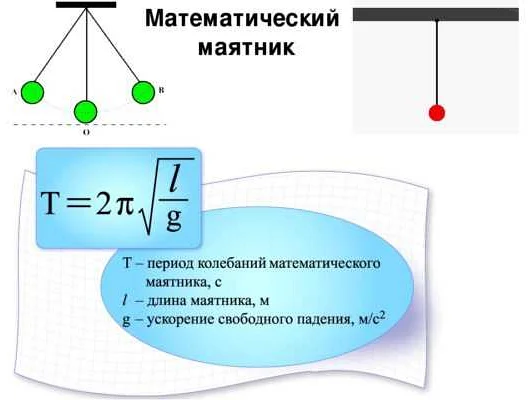
Маятник — одно из самых простых и удивительных явлений в мире физики. Его движение можно описать с помощью простых математических уравнений, и маятник играет важную роль во многих областях науки и техники. Одним из основных параметров маятника является его длина, которая оказывает прямое влияние на его период колебаний — время, за которое маятник совершает один полный цикл.

Период колебаний математического маятника зависит от его длины и силы тяжести. Для идеального математического маятника без трения или сопротивления воздуха период колебаний можно выразить следующей формулой:

T = 2π√(L/g)

где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

Если нам известен период колебаний и ускорение свободного падения, мы можем выразить длину математического маятника. Пусть период колебаний равен 2 секунды, а ускорение свободного падения примерно равно 9.8 м/с^2. Подставим эти значения в формулу и найдем длину математического маятника:

L = (T/(2π))^2 * g

Определение периода колебаний

Для определения периода колебаний математического маятника можно использовать различные методы. Один из таких методов основан на измерении времени, за которое маятник совершает несколько полных колебаний. Затем это время делится на количество совершенных колебаний, и получается среднее время одного колебания, то есть период.

Для измерения времени колебаний можно использовать секундомер или другие точные временные приборы. Например, можно запустить секундомер в момент, когда маятник проходит через положение равновесия, и остановить его, когда маятник снова вернется в это положение. Затем измеренное время делится на количество совершенных колебаний, и получается период.

Для достижения более точного результата можно повторить измерения несколько раз и усреднить полученные значения. Также можно изменять длину маятника и проводить измерения для разных длин, чтобы установить зависимость периода колебаний от длины.

Длина маятникаПериод колебаний

1 м	2 с
2 м	2.83 с
3 м	3.46 с

Из таблицы видно, что с увеличением длины маятника период колебаний также увеличивается. Это связано с тем, что при большей длине маятника гравитационная сила, действующая на него, больше, и он требует большего времени для прохождения полного цикла колебаний.

Математический маятник и его характеристики

Одной из основных характеристик математического маятника является его длина. Длина маятника определяет период его колебаний, то есть время, за которое маятник совершает полный цикл движения. Чем длиннее маятник, тем дольше будет его период колебаний.

В данном случае, длина математического маятника, при которой его период колебаний составляет 2 секунды, имеет особую значимость. Из этой характеристики можно определить период колебаний для других длин маятника, используя математическую формулу.

Важно отметить, что математический маятник идеализированная модель, которая не учитывает воздействие сопротивления воздуха и других факторов. В реальности, маятник будет останавливаться из-за сил трения и других внешних воздействий, поэтому его движение будет ограничено.

Формула для расчета периода колебаний

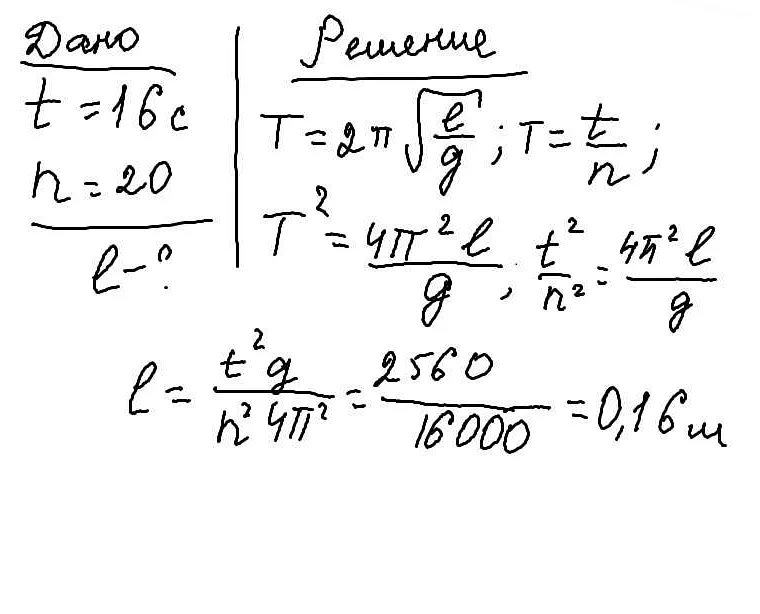
Период колебаний математического маятника может быть вычислен с использованием следующей формулы:

Период колебаний T (в секундах) зависит от длины маятника L (в метрах) и ускорения свободного падения g (в метрах в секунду в квадрате) по следующему правилу:

T = 2π√(L/g)

Данная формула позволяет определить длину математического маятника, если известны его период колебаний и ускорение свободного падения.

Например, для математического маятника с периодом колебаний 2 секунды можно использовать данную формулу для расчета его длины. При известном ускорении свободного падения (около 9,8 м/с² на поверхности Земли) можно вычислить длину маятника.

Влияние длины маятника на период колебаний

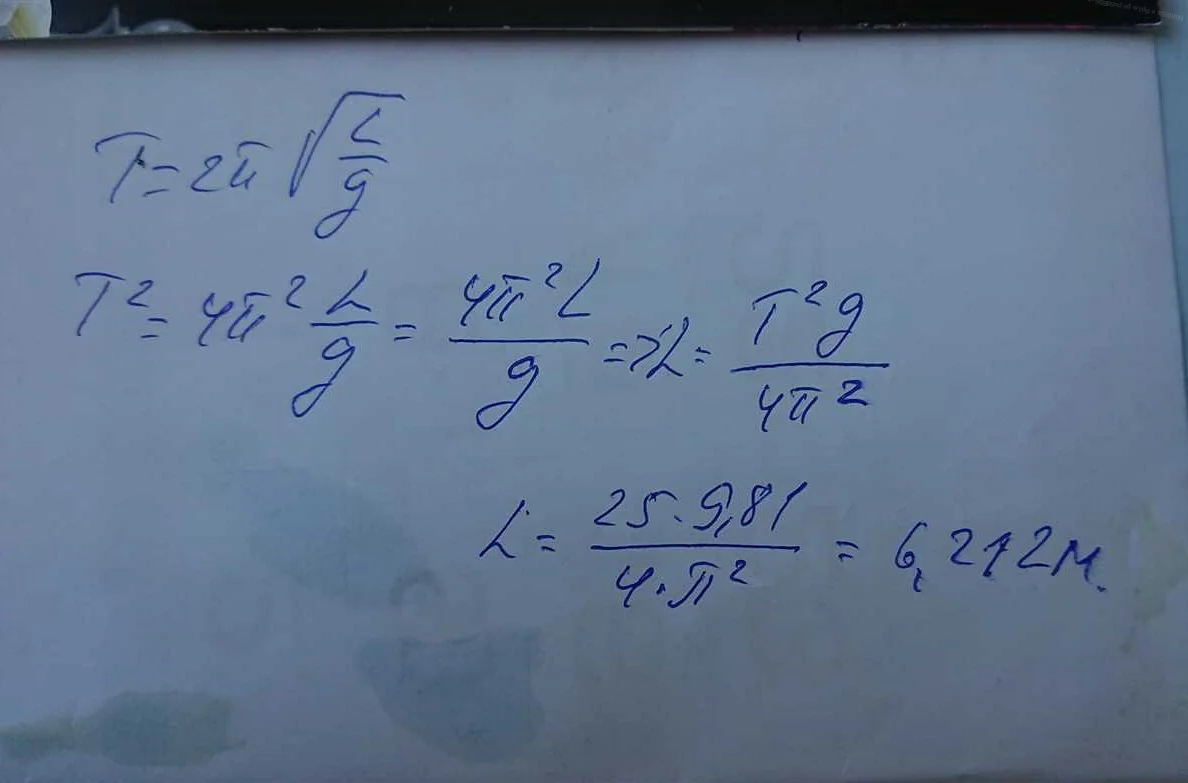
Период колебаний математического маятника — это время, за которое маятник делает одну полную осцилляцию, то есть проходит через точку равновесия дважды. Величина периода обратно пропорциональна квадратному корню из длины маятника.

Формула для расчета периода колебаний математического маятника:

Длина маятника (L)Период колебаний (T)

1 метр	2 секунды
2 метра	2.83 секунды
3 метра	3.46 секунды
4 метра	4 секунды
5 метров	4.47 секунды

Из таблицы видно, что с увеличением длины маятника, период колебаний также увеличивается. Это объясняется тем, что при большей длине маятника требуется больше времени для его прохождения через полный цикл колебаний.

Исследование влияния длины маятника на период колебаний имеет практическое применение в различных областях, таких как физика, инженерия и архитектура. Знание зависимости периода колебаний от длины маятника позволяет оптимизировать работу различных механизмов и конструкций, основанных на принципе математического маятника.

Как определить длину маятника для заданного периода?

Длина математического маятника имеет важное значение для определения его периода колебаний. Период колебаний маятника зависит от его длины и ускорения свободного падения. Для заданного периода колебаний можно определить необходимую длину маятника.

Формула для определения периода колебаний математического маятника:

T = 2π√(L/g)

Где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

Для определения длины маятника для заданного периода нужно использовать обратную формулу:

L = (T/(2π))² * g

Для расчета длины маятника необходимо знать заданный период колебаний и значение ускорения свободного падения. Подставив эти значения в формулу, можно определить длину маятника, которая будет обеспечивать заданный период.

Расчет длины математического маятника

Длина математического маятника с периодом колебаний 2 секунды может быть рассчитана с помощью формулы:

l = g * T2 / (4 * π2)

Где:

• l — длина математического маятника;
• g — ускорение свободного падения (около 9.8 м/с2 на Земле);
• T — период колебаний (в данном случае 2 секунды);
• π — математическая константа, приближенно равная 3.14159.

Подставив известные значения в формулу, можно вычислить длину математического маятника:

ПараметрЗначение

g	9.8 м/с2
T	2 секунды
π	3.14159
l	?

Подставим значения и выполним вычисления:

l = 9.8 * 22 / (4 * 3.141592)

l ≈ 0.986 метров

Таким образом, длина математического маятника с периодом колебаний 2 секунды составляет примерно 0.986 метров.

Примеры расчета длины маятника для периода 2 секунды

Длина математического маятника зависит от его периода колебаний и гравитационного ускорения.

Для расчета длины маятника с периодом колебаний 2 секунды можно использовать формулу:

T = 2π√(l/g)

где T — период колебаний маятника, l — длина маятника, g — гравитационное ускорение.

Подставим известные значения в формулу:

2 = 2π√(l/g)

Для упрощения выражения можно возвести обе части уравнения в квадрат:

4 = 4π²(l/g)

Теперь можно сократить на 4 и π²:

1 = l/g

Таким образом, для маятника с периодом 2 секунды длина маятника равна гравитационному ускорению.

Применение математического маятника в науке и технике

В научных исследованиях математического маятника используются для измерения различных физических величин. Например, длина математического маятника может быть использована для определения ускорения свободного падения на Земле. Измеряя период колебаний маятника, можно рассчитать его длину и затем использовать формулу ускорения свободного падения для определения значений этой физической величины.

Математические маятники также применяются в технике, например, в часах и метрологических устройствах. Их точность и стабильность колебаний позволяют использовать их для измерения времени или других параметров. Маятники могут быть сделаны очень точными и устойчивыми к внешним воздействиям, что делает их незаменимыми инструментами в науке и технике.

ПрименениеПримеры

Научные исследования	Измерение ускорения свободного падения
Техника	Часы, метрологические устройства

Вопрос-ответ:

Какая формула позволяет рассчитать длину математического маятника с заданным периодом колебаний?

Формула для рассчета длины математического маятника с заданным периодом колебаний имеет вид: L = gT^2 / (4π^2), где L — длина маятника, g — ускорение свободного падения (примерно 9.8 м/с^2), T — период колебаний.

Какова длина математического маятника, если его период колебаний составляет 2 секунды?

Если период колебаний математического маятника составляет 2 секунды, то его длина может быть рассчитана по формуле: L = gT^2 / (4π^2) = 9.8 * (2^2) / (4 * 3.14^2) ≈ 0.985 метра.

Какой период колебаний будет у математического маятника длиной 1 метр?

Период колебаний математического маятника можно рассчитать по формуле: T = 2π * √(L / g), где L — длина маятника, g — ускорение свободного падения (примерно 9.8 м/с^2). Подставляя в формулу значения, получим: T = 2 * 3.14 * √(1 / 9.8) ≈ 2 * 3.14 * 0.316 ≈ 1.99 секунды.

Как изменится период колебаний математического маятника, если его длину увеличить вдвое?

Если увеличить длину математического маятника вдвое, то его период колебаний увеличится в √2 раза. Например, если исходный период колебаний составлял 2 секунды, то после увеличения длины вдвое период станет равным примерно 2 * √2 ≈ 2.828 секунды.

Какую длину должен иметь математический маятник, чтобы его период колебаний составлял 1 секунду?

Длину математического маятника, при которой его период колебаний составляет 1 секунду, можно рассчитать по формуле: L = gT^2 / (4π^2) = 9.8 * (1^2) / (4 * 3.14^2) ≈ 0.248 метра.

Видео по теме: