Что такое дополнительные лучи 5 класс математика
Содержимое
- 1 Что такое дополнительные лучи 5 класс математика
- 1.1 Что такое дополнительные лучи в математике?
- 1.2 Определение дополнительных лучей
- 1.3 Как обозначаются дополнительные лучи?
- 1.4 Какие свойства имеют дополнительные лучи?
- 1.5 Примеры использования дополнительных лучей
- 1.6 Дополнительные лучи и углы
- 1.7 Вопрос-ответ:
- 1.8 Задачи с дополнительными лучами
- 1.9 Видео по теме:
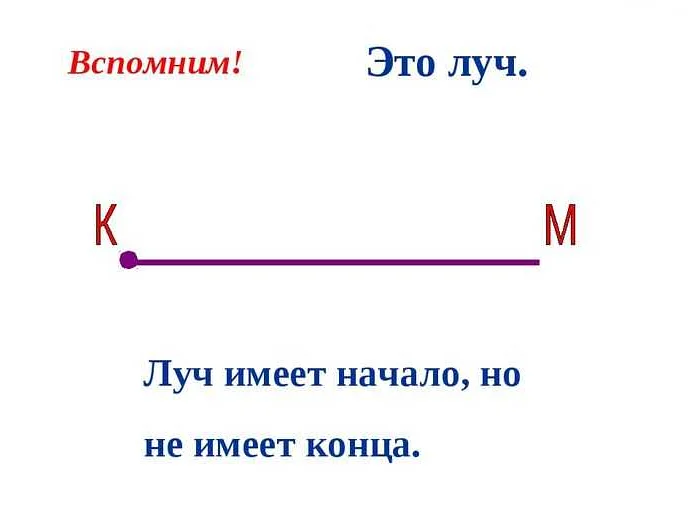
Дополнительные лучи в математике 5 класса — это лучи, которые исходят из одной и той же точки, но направлены в разные стороны. Они являются частью изучения геометрии и помогают учащимся понять основные понятия, такие как луч, точка и прямая. В этой статье мы рассмотрим основные свойства дополнительных лучей и приведем примеры их применения в задачах.
Дополнительные лучи – это особый тип лучей, которые выходят из одной точки и распространяются в одном направлении, но не ограничены одной прямой. Они имеют общую начальную точку, но не ограничены в длине и могут распространяться бесконечно в одном направлении.
В математике дополнительные лучи обычно обозначаются буквами латинского алфавита со стрелочкой сверху. Начальная точка луча обозначается заглавной буквой, например, луч AB, луч CD. Дополнительный луч обозначается добавлением символа стрелки над буквой, например, луч AB̄, луч CD̄.
Примеры использования дополнительных лучей в математике могут быть разнообразными. Они могут применяться для определения углов, для построения геометрических фигур, а также для обозначения направления движения или распространения. Важно помнить, что дополнительные лучи продолжаются бесконечно в одном направлении и не имеют конечной точки.
Что такое дополнительные лучи в математике?
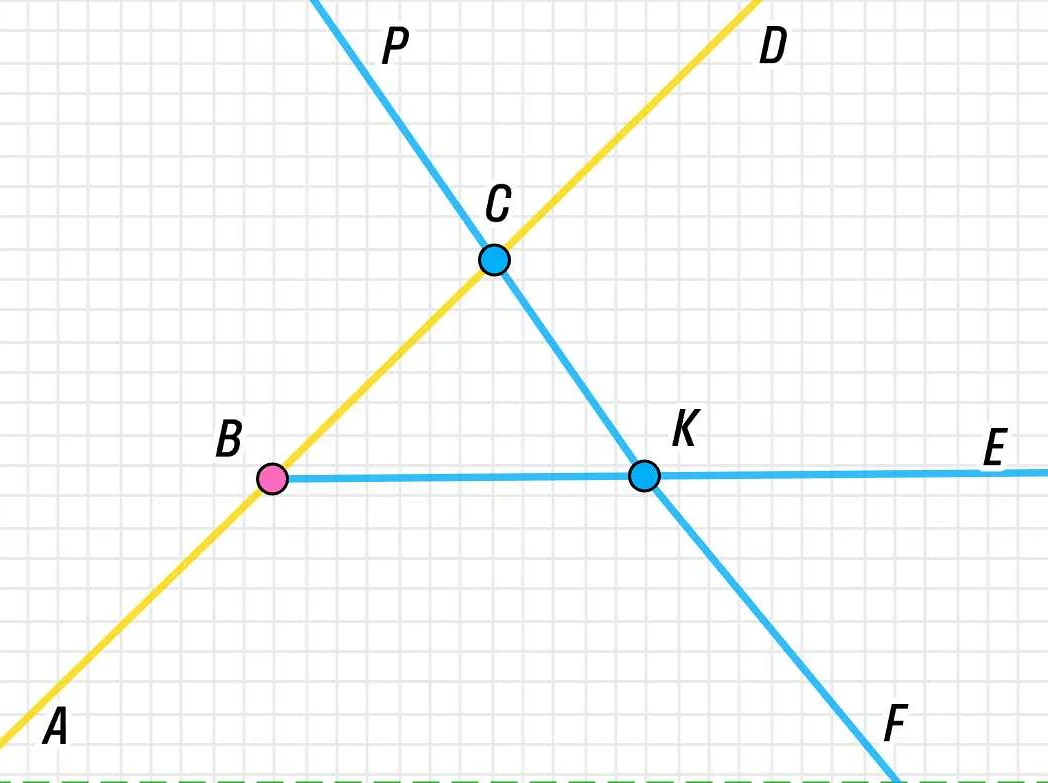
Дополнительные лучи являются важным понятием в геометрии. Они используются для изучения и определения различных видов углов, таких как прямой угол, острый угол, тупой угол и др.
Дополнительные лучи могут быть представлены в виде графических изображений или обозначены буквами и символами. Например, два дополнительных луча могут быть обозначены как луч AB и луч BC, где точка B является общим началом.
Примеры использования дополнительных лучей включают определение и измерение углов, решение геометрических задач, построение и нахождение пересечений линий и т.д.
Изучение дополнительных лучей помогает учащимся развивать навыки визуального восприятия, анализа и решения геометрических задач. Это также содействует логическому мышлению и развитию математической интуиции.
Определение дополнительных лучей
Основной луч — это первый луч, который идет из общего начала и продолжается вперед. Дополнительный луч — это второй луч, который идет из общего начала, но в противоположном направлении.
Дополнительные лучи обычно обозначаются буквами, например, AB и CD. Они могут быть расположены в любом положении и направлении, но всегда имеют общее начало.
Дополнительные лучи могут быть использованы для измерения углов, поскольку они образуют прямую линию вместе. Они также могут быть использованы для определения положения объектов на плоскости.
Примеры дополнительных лучей:
- AB и BC — основной луч AB продолжается вперед, а дополнительный луч BC идет в противоположном направлении;
- DE и EF — основной луч DE продолжается вперед, а дополнительный луч EF идет в противоположном направлении;
- MN и NO — основной луч MN продолжается вперед, а дополнительный луч NO идет в противоположном направлении.
Как обозначаются дополнительные лучи?
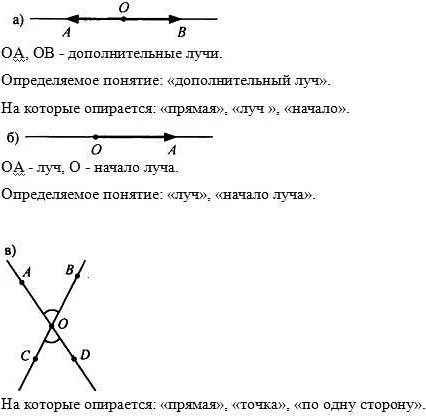
Обозначение дополнительных лучей помогает нам легко идентифицировать и различать их при решении задач и построении геометрических фигур. Например, если нам даны лучи А и В и говорится, что луч В является дополнительным к лучу А, мы можем использовать их обозначения для понимания и решения задачи.
ЛучОбозначениеДополнительный лучОбозначение
| А | AB | В качестве дополнительного луча к А | B̅ |
| CD | CD | В качестве дополнительного луча к CD | D̅ |
Таким образом, обозначение дополнительных лучей помогает нам легко определять и работать с ними в математических задачах и геометрических построениях.
Какие свойства имеют дополнительные лучи?

1. Продолжение: Дополнительные лучи продолжаются бесконечно в одном направлении. Это означает, что они не имеют конечного конца и могут быть продолжены в одном направлении.
2. Параллельность: Дополнительные лучи, по определению, параллельны исходному лучу. Это означает, что они имеют одинаковое направление и никогда не пересекаются.
3. Единственность: Дополнительный луч — это только одно продолжение исходного луча. Он не должен пересекаться с другими лучами и иметь несколько продолжений.
4. Именование: Дополнительные лучи обычно именуются с использованием двух букв: одна буква обозначает начальную точку, а вторая буква — направление продолжения.
Например, если исходный луч называется «a», то его дополнительные лучи могут быть обозначены как «ab» и «ac», где «b» и «c» — это точки, принадлежащие дополнительным лучам.
Зная эти свойства, мы можем использовать дополнительные лучи для анализа и построения геометрических фигур и решения различных задач в математике.
Примеры использования дополнительных лучей
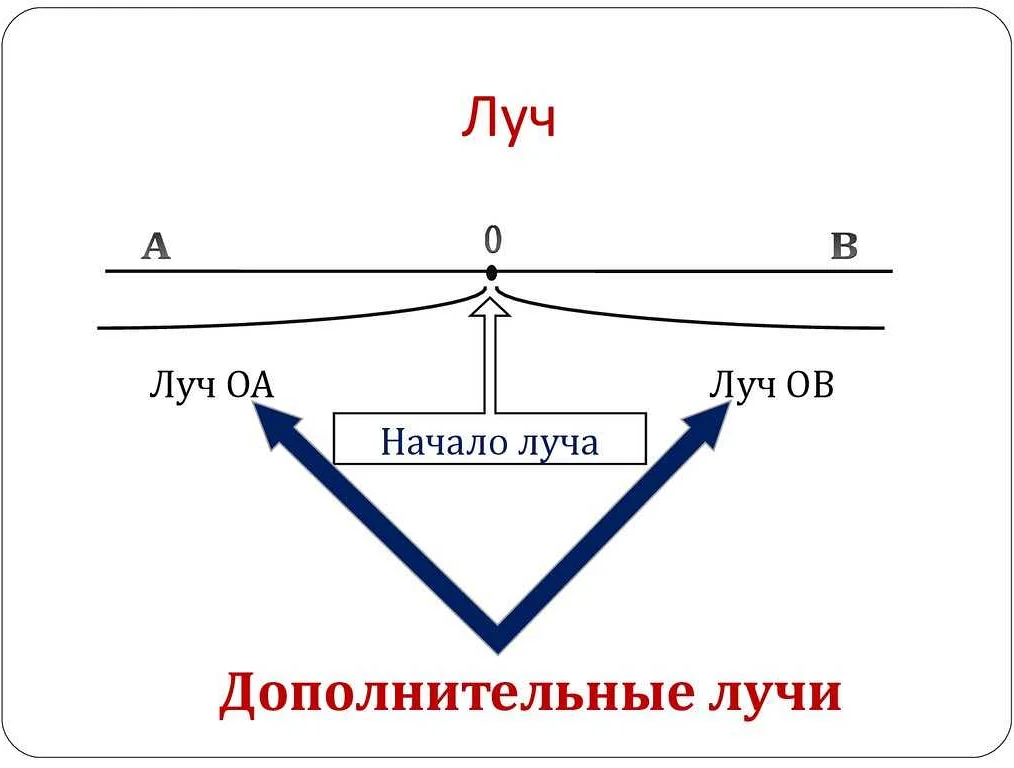
Пример 1:
Представим, что у нас есть два перпендикулярных луча AB и CD. Дополнительный луч AE образуется при продолжении луча AB за точку B. Точка E находится на продолжении луча AB.
Теперь представим, что точка F находится на продолжении луча CD. Дополнительный луч CF образуется при продолжении луча CD за точку D.
Таким образом, мы получаем два дополнительных луча AE и CF, которые образуют две пары вертикальных углов: угол AED и угол CEF, угол BEC и угол ADF.
Пример 2:
Рассмотрим треугольник ABC. Представим, что у нас есть луч DE, который проходит через вершину B и делит угол ABC на два угла. Это дополнительный луч, так как он продолжает одну из сторон угла ABC.
Точка D может находиться как внутри угла ABC, так и вне его. Если точка D находится внутри угла ABC, то угол DBE будет дополнительным углом к углу ABC.
Если точка D находится вне угла ABC, то угол EBC будет дополнительным углом к углу ABC.
Пример 3:
Представим, что у нас есть два пересекающихся луча. Луч AB и луч CD пересекаются в точке O.
Дополнительные лучи AO и CO образуют две пары вертикальных углов: угол AOC и угол BOE, угол COB и угол AOE. Дополнительные лучи EO и BO также образуют две пары вертикальных углов: угол BOE и угол COB, угол AOE и угол AOC.
Таким образом, дополнительные лучи позволяют нам рассматривать различные углы, образованные пересекающимися лучами или продолжением лучей за точкой пересечения.
Дополнительные лучи и углы
Дополнительные углы всегда суммируются до 180 градусов. Если у нас есть два дополнительных угла, один из которых измеряет 60 градусов, то другой угол будет измерять 120 градусов, чтобы в сумме получилось 180 градусов.
Дополнительные лучи и углы широко используются в геометрии для решения различных задач. Например, если у нас есть параллельные линии и пересекающая их прямая, то полученные дополнительные углы будут равными. Это свойство дополнительных углов помогает нам решать задачи на нахождение неизвестных углов и длин сторон в геометрических фигурах.
Ниже приведена таблица с примерами дополнительных углов:
Угол 1Угол 2Сумма углов
| 30 градусов | 150 градусов | 180 градусов |
| 45 градусов | 135 градусов | 180 градусов |
| 90 градусов | 90 градусов | 180 градусов |
Использование дополнительных лучей и углов помогает нам лучше понять и анализировать геометрические фигуры и свойства линий. Эти концепции являются основополагающими для более сложных тем в геометрии и широко применяются в решении задач и построении доказательств.
Вопрос-ответ:
Зачем нужны дополнительные лучи в математике?
Дополнительные лучи используются в математике для обозначения отрезков, которые продолжаются в одном направлении бесконечно. Они помогают нам упростить запись геометрических объектов и сделать ее более компактной.
Как определить дополнительные лучи?
Дополнительные лучи определяются двумя точками — начальной и конечной. Начальная точка указывается с помощью обозначения точки, а конечная точка — с помощью стрелки, указывающей направление продолжения луча.
Можете привести примеры использования дополнительных лучей?
Конечно! Например, если нам нужно обозначить луч AB, который продолжается вправо, мы можем записать его с помощью символа AB с правой стрелкой. Также, если нам нужно обозначить луч CD, который продолжается влево, мы можем записать его с помощью символа CD с левой стрелкой.
Какие свойства имеют дополнительные лучи?
Дополнительные лучи не имеют фиксированной длины, они продолжаются в выбранном направлении бесконечно. Также, их можно параллельно сдвигать, сохраняя направление и бесконечность.
Задачи с дополнительными лучами

Дополнительные лучи имеют особые свойства, которые позволяют решать задачи с использованием геометрических принципов.
Пример 1:
На плоскости даны два дополнительных луча и точка, лежащая внутри угла между ними. Найдите меру угла между этими лучами.
Исходные данныеРешение
| Дополнительные лучи | AB, AC |
| Точка | P |
| Известно | Угол BAP = 30° |
| Найти | Угол BAC |
| Решение | Угол BAC = Угол BAP + Угол PAC |
| Угол BAC = 30° + Угол PAC | |
| Угол PAC = Угол BAC — 30° | |
| Угол PAC = Угол BAC — 30° = Угол BAC — 30° = 60° |
Ответ: Угол BAC равен 60°.
Пример 2:
На плоскости даны два пересекающихся дополнительных луча и точка пересечения. Найдите меру каждого из углов, образованных этими лучами.
Исходные данныеРешение
| Пересекающиеся дополнительные лучи | AB, AC |
| Точка пересечения | P |
| Известно | Нет |
| Найти | Угол BAP, Угол PAC |
| Решение | Угол BAP = Угол PAC (так как они вертикальные) |
| Угол BAP = Угол PAC = 90° |
Ответ: Угол BAP и угол PAC равны 90° каждый.
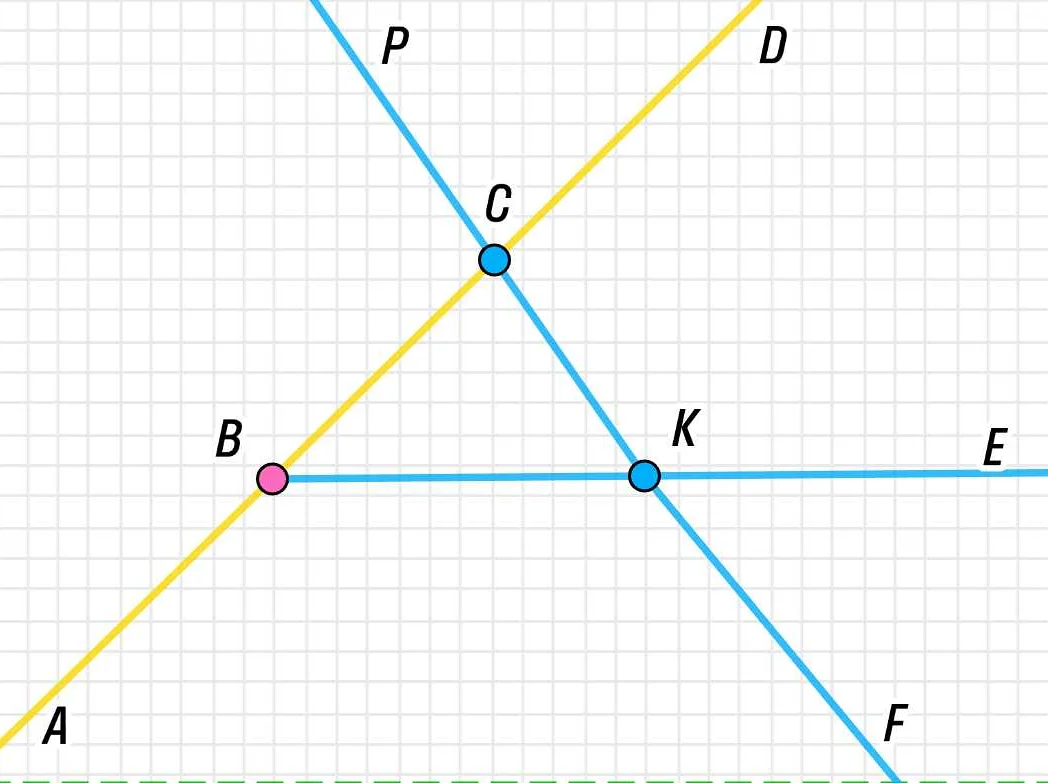

Статья очень понятно и доступно объясняет, что такое дополнительные лучи в математике. Я, как родитель, был приятно удивлен, как изложена информация для пятого класса. Теперь я могу с легкостью объяснить своему ребенку, что такое дополнительные лучи и как их использовать. А примеры, приведенные в статье, сразу проиллюстрировали, как можно использовать дополнительные лучи для решения задач. Спасибо автору за понятное и полезное объяснение! Теперь мой ребенок сможет легко разобраться в этой теме и успешно справиться со своими математическими заданиями.