Что такое интегрирование в математике простыми словами

Интегрирование в математике — это процесс нахождения площади под графиком функции. Узнайте, как работает интегрирование и как его использовать в решении математических задач.

Интегрирование — одно из важнейших понятий в математике, которое часто вызывает затруднения у студентов. В простых словах, интегрирование означает нахождение площади под кривой на графике функции. Это полезное умение, которое находит применение во многих областях — от физики до экономики. Объяснить интегрирование можно с помощью нескольких основных концепций и приемов.

Основное понятие интеграла — это площадь под кривой. Для нахождения этой площади используется процесс интегрирования. Он состоит в том, чтобы разбить кривую на бесконечно малые отрезки и найти сумму площадей прямоугольников, которыми эти отрезки заменяются. Чем мельче отрезки, тем точнее будет результат. Для этого используется понятие предела, которое позволяет учесть все маленькие изменения на кривой.

Интеграл — это не просто площадь под кривой, это также способ определить изменение величины, описываемой кривой. Например, если кривая описывает изменение скорости, то интеграл от этой кривой даст тебе пройденное расстояние.

Основной метод интегрирования — это нахождение первообразной функции. Первообразная функция — это функция, производная которой равна исходной функции. Другими словами, если ты найдешь первообразную функцию для заданной функции, то сможешь найти ее интегралы для любых значений переменной. Это очень удобно, так как позволяет избежать сложных вычислений и повторять одни и те же шаги для разных значений.

Интегрирование — это не только математический инструмент, но и мощный метод анализа данных. Оно позволяет находить связи между различными факторами и делать прогнозы. Понимание основных концепций интегрирования поможет тебе лучше понять и применить этот метод в практических задачах и исследованиях.

Что такое интегрирование в математике и зачем оно нужно?

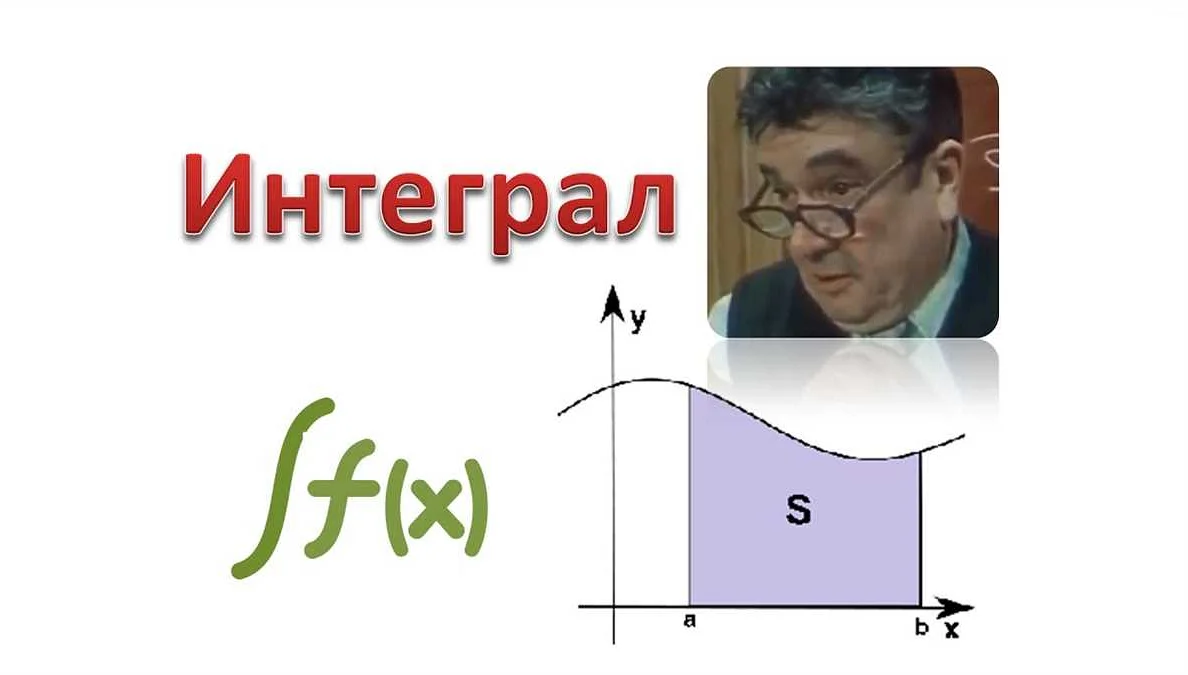
Интеграл — это математический объект, который обозначается символом ∫. Он представляет собой обратную операцию к дифференцированию и позволяет находить функции, которые являются первообразными (антипроизводными) для заданной функции.

Интегрирование имеет множество практических применений. Например, с помощью интегралов можно найти площадь фигуры, ограниченной графиком функции и осями координат. Также интегралы позволяют находить объемы тел, заданных графиками функций, и решать задачи, связанные с накоплением величин, например, вычислять суммарное количество товаров на складе или изменение количества вещества в химической реакции.

Интегрирование также используется для решения дифференциальных уравнений, которые описывают зависимости между неизвестной функцией и ее производными. Путем интегрирования дифференциального уравнения можно найти функцию, удовлетворяющую этому уравнению и описывающую интересующий процесс или явление.

Применение интегрирования:Пример

Вычисление площади фигуры	Найти площадь круга с радиусом 5
Вычисление объема тела	Найти объем цилиндра с высотой 10 и радиусом основания 3
Решение задачи накопления	Найти количество денег на счете после 3 лет при годовой процентной ставке 5%
Решение дифференциального уравнения	Найти функцию, описывающую зависимость скорости от времени при известной ускорении

Без интегрирования невозможно точно решить множество практических задач, связанных с нахождением площадей, объемов, накопления и изменения величин. Интегралы играют важную роль в математике и науке в целом, обеспечивая точные и удобные методы решения сложных задач.

Понятие интегрирования в математике

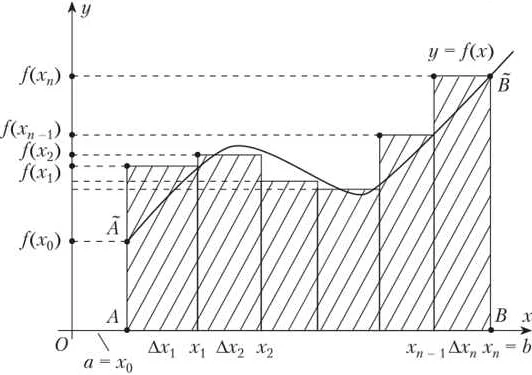
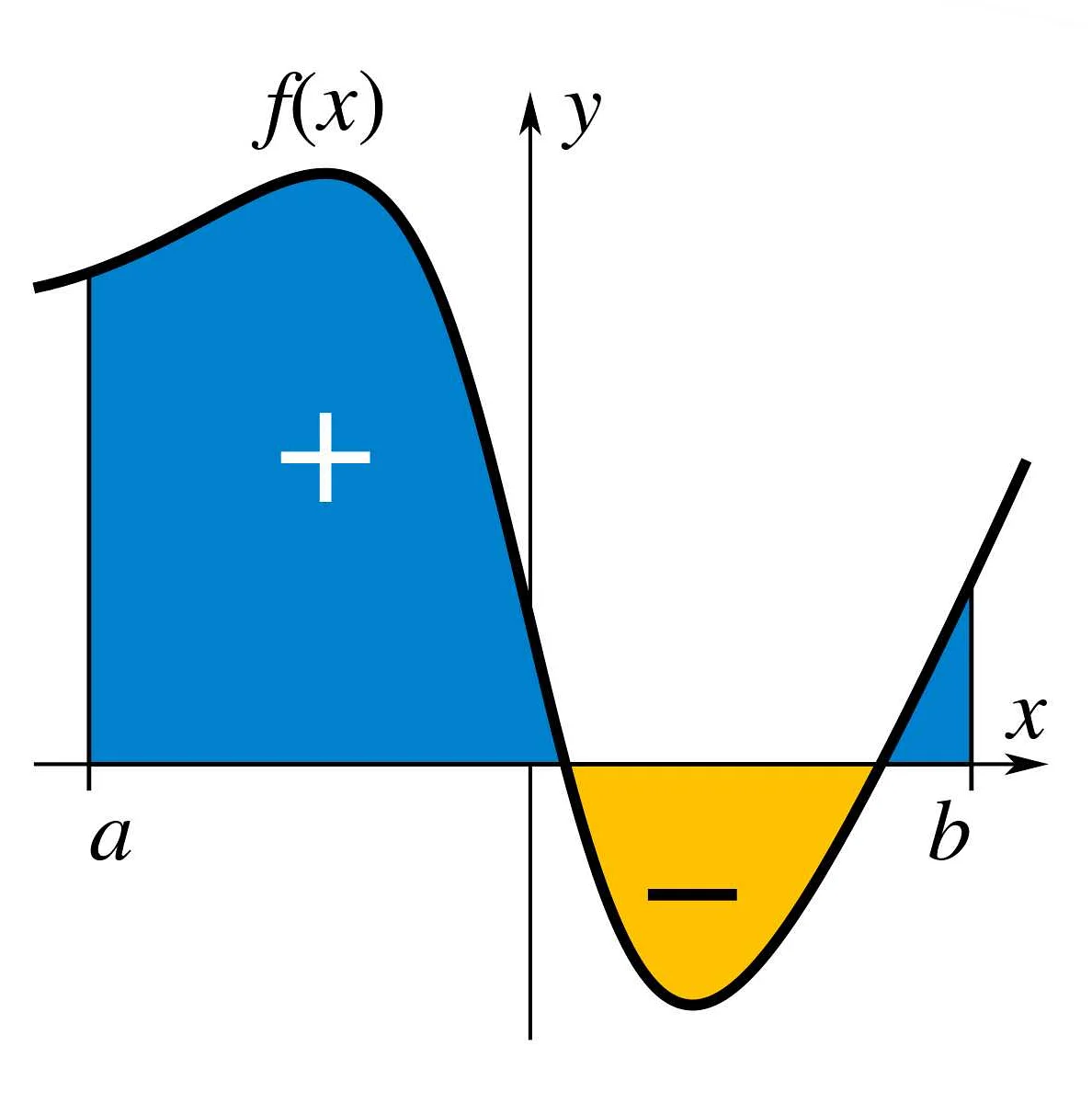
Идея интегрирования заключается в том, чтобы разбить заданную область на бесконечно маленькие элементы и приближенно вычислить сумму их площадей. Для этого используется понятие определенного интеграла.

Определенный интеграл обозначается знаком ∫ и состоит из двух пределов интегрирования и подынтегральной функции. Верхний предел интегрирования обозначает конечную точку области, а нижний предел — начальную точку области. Подынтегральная функция задает кривую, под которой вычисляется площадь.

СимволОписание

∫	знак интеграла
dx	дифференциал x
a	нижний предел интегрирования
b	верхний предел интегрирования
f(x)	подынтегральная функция

Интегралы позволяют находить площади, объемы, центры тяжести, массы и другие важные характеристики геометрических фигур. Они также находят широкое применение в физике, экономике, статистике и других областях науки.

Какие задачи решает интегрирование?

1. Нахождение площади под кривой. Интегрирование позволяет вычислить площадь ограниченной кривой и осями координат.
2. Нахождение объема тела. С помощью интегрирования можно вычислить объем сложной фигуры, например, тела вращения.
3. Нахождение среднего значения функции. Интегрирование позволяет найти среднее значение функции на отрезке.
4. Нахождение работы силы. Интегрирование используется для вычисления работы, совершаемой силой при перемещении объекта.
5. Нахождение центра масс. Интегрирование позволяет найти координаты центра масс сложной системы.

Это лишь некоторые примеры задач, которые можно решить с помощью интегрирования. Оно широко применяется в физике, экономике, статистике и других областях, где требуется анализ и вычисление различных величин. Интегрирование позволяет увидеть глубину и скрытые закономерности в данных и явлениях, что делает его неотъемлемой частью математики и науки в целом.

Основные методы интегрирования

Основные методы интегрирования включают:

МетодОписание

Метод замены переменной	Замена переменной позволяет свести сложный интеграл к более простой форме.
Метод интегрирования по частям	Этот метод применяется для интегрирования произведения двух функций.
Метод разложения на простые дроби	Используется для интегрирования рациональных функций.
Метод интегрирования дробно-рациональных функций	Используется для интегрирования функций, содержащих дроби.
Метод тригонометрических замен	Этот метод используется для интегрирования функций, содержащих тригонометрические функции и их обратные функции.
Метод неопределенных коэффициентов	Данный метод применяется для интегрирования функций, которые не могут быть интегрированы с помощью других методов.

Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной задачи. Знание и умение применять различные методы интегрирования позволяет решать сложные математические задачи и находить аналитические решения.

Примеры применения интегрирования в реальной жизни

1. Физика и механика:

Интегрирование широко применяется в физике и механике для решения различных задач. Например, для определения пути, пройденного телом с заданной скоростью или для расчета массы объекта по известной зависимости силы от времени.

2. Экономика:

В экономике интегрирование используется для моделирования экономических процессов и анализа данных. Например, для определения общего объема производства или для расчета прибыли от изменения цен на товары.

3. Медицина:

В медицине интегрирование может быть применено для анализа данных о здоровье пациентов, например, для определения изменения давления или для расчета объема лекарственного вещества в организме.

4. Космология:

В космологии интегрирование используется для моделирования движения планет и других космических объектов. Например, для определения орбиты спутника или для расчета времени полета космического корабля.

Все эти примеры демонстрируют важность и широкий спектр применения интегрирования в различных областях науки и техники.

Практическое применение интегрирования в различных областях

В физике интегрирование используется для определения силы, потока энергии и работы. Например, чтобы найти работу, необходимую для перемещения объекта по заданному пути, можно воспользоваться интегралом. Также интегрирование помогает определить массу тела или распределение массы в пространстве.

В экономике интегрирование используется для определения общих издержек, доходов и прибыли. Оно также позволяет вычислять интегральный показатель, такой как индекс цен, что помогает анализировать экономическую ситуацию.

В медицине интегрирование применяется для моделирования физиологических процессов в организме, обработки медицинских изображений и анализа данных. Например, интегрирование может помочь вычислить общую площадь под кривой, что является важным для определения площади под графиком зависимости концентрации лекарства от времени.

В технике интегрирование используется для моделирования и анализа различных процессов. Например, интегрирование помогает определить объемы материалов, необходимых для строительства, или электрическую мощность, потребляемую при работе электронного устройства.

Таким образом, интегрирование является важным инструментом в различных областях, где оно помогает решать задачи, связанные с вычислением площадей, объемов, центров тяжести и других характеристик объектов и процессов.

Основные правила интегрирования

Для выполнения интегрирования существуют основные правила, которые помогают упростить процесс и получить точный результат:

1. Линейность. Интеграл от суммы двух функций равен сумме интегралов каждой из функций по отдельности. То есть, если f(x) и g(x) интегрируемы на некотором отрезке, то интеграл от (f(x) + g(x)) равен сумме интегралов от f(x) и g(x).
2. Правило постоянного множителя. Интеграл от произведения функции на постоянное число равен произведению этого числа на интеграл от функции.
3. Правило замены переменной. Если в интеграле присутствует функция u(x), которая может быть выражена через другую переменную t, то интеграл можно переписать с новой переменной и выполнить интегрирование по новому уравнению.
4. Интегрирование по частям. Используется для интегрирования произведения двух функций. Интеграл от произведения функций f(x) и g(x) равен произведению g(x) на интеграл от f(x), минус интеграл от произведения производной g'(x) и функции f(x).
5. Интегрирование простейших функций. Для некоторых простейших функций существуют известные правила интегрирования. Например, интеграл от константы равен константе, интеграл от x в степени n равен x в степени n+1, деленному на (n+1).

Эти основные правила интегрирования помогают решать математические задачи, связанные с определением площадей, нахождением средних значений и других важных величин.

Вопрос-ответ:

Что такое интегрирование?

Интегрирование — это процесс нахождения функции, которая является первообразной для данной функции. В математике интегрирование используется для решения задач, связанных с площадью, объемом, скоростью и другими величинами.

Зачем нужно интегрирование в математике?

Интегрирование в математике имеет широкий спектр применений. Оно позволяет находить площади под кривыми, объемы тел, работу, среднюю величину и другие важные параметры. Интегралы также используются для решения дифференциальных уравнений и моделирования различных физических явлений.

Как происходит интегрирование?

Интегрирование происходит путем нахождения неопределенного или определенного интеграла от функции. Неопределенный интеграл даёт общую функцию, которая является первообразной для данной функции. Определенный интеграл находит числовое значение интеграла на заданном интервале.

Чем отличается интегрирование от дифференцирования?

Интегрирование и дифференцирование — это две взаимообратные операции в математическом анализе. Дифференцирование находит производную функции, позволяя определить скорость изменения функции в каждой точке. Интегрирование, напротив, находит первообразную функции, позволяя найти исходную функцию по её производной.

Свойства интеграла и их применение

Линейность интеграла:

Если функции f(x) и g(x) интегрируемы на отрезке [a, b], а k – произвольная константа, то верно следующее:

∫[a, b] (kf(x) + g(x)) dx = k∫[a, b] f(x) dx + ∫[a, b] g(x) dx

То есть интеграл от линейной комбинации функций равен линейной комбинации интегралов от этих функций.

Аддитивность интеграла:

Если функция f(x) интегрируема на отрезках [a, c] и [c, b], то:

∫[a, b] f(x) dx = ∫[a, c] f(x) dx + ∫[c, b] f(x) dx

То есть интеграл от функции на отрезке [a, b] равен сумме интегралов от этой функции на отрезках [a, c] и [c, b].

Теорема о среднем значении:

Если функция f(x) непрерывна на отрезке [a, b], то существует такая точка c ∈ [a, b], что:

∫[a, b] f(x) dx = f(c) ∙ (b — a)

То есть интеграл от непрерывной функции на отрезке [a, b] равен произведению значения функции в некоторой точке на длину этого отрезка.

Свойства интеграла позволяют решать различные задачи, например, вычислять площади под графиками функций, находить значения определенных интегралов и решать дифференциальные уравнения. Они являются важным инструментом в математическом анализе и находят широкое применение в различных областях науки и техники.

Видео по теме: