Кто создал математическую логику

Математическая логика была создана группой ученых в XIX веке. Одним из главных создателей считается Джордж Буль. В статье рассмотрены его вклад и вклад других ученых в развитие математической логики.

Математическая логика является одной из важнейших областей математики, изучающей формальные системы и их свойства. Она исследует методы и правила, которые позволяют строить верные математические доказательства, а также разрабатывает формальные языки для описания математических объектов и отношений между ними.

История математической логики началась в XIX веке, когда математики стали задумываться над основаниями своей науки. Одной из ключевых фигур в развитии математической логики стал немецкий математик Георг Кантор, который внес значительный вклад в теорию множеств и разработал понятие бесконечности.

В начале XX века история математической логики была резко ускорена работами логиков, таких как Бертран Рассел и Альфред Норт Уайтхед. Они стремились создать формальную систему, основанную на логике, которая могла бы использоваться для доказательства всех математических утверждений. В результате своих исследований они создали логический аппарат, известный как «Принцип Математики».

«Математика — это наука обо всем, что может быть выведено из трех аксиом: аксиомы вывода, аксиомы тождества и аксиомы индукции.» — Георг Кантор, основатель теории множеств.

Следующим важным этапом в истории математической логики стала работа американского логика Курта Геделя. В 1931 году он опубликовал свою теорему о неполноте, которая показала ограничения формальных систем и невозможность создать систему, которая могла бы доказать все математические истины. Эта теорема имела огромное значение для развития математической логики и позволила логикам более глубоко понять ее основы.

С тех пор история математической логики продолжается, исследуя более сложные и абстрактные математические структуры, разрабатывая новые формальные системы и методы доказательств. Работы таких ученых, как Алонзо Чёрч и Алан Тьюринг, стали основой для развития компьютерной науки и искусственного интеллекта.

Математическая логика: становление и развитие

Одним из основных этапов развития математической логики было создание и формализация математической арифметики. Именно в арифметике математики столкнулись с противоречиями и неоднозначностями, которые требовали строгого логического обоснования. В этот период были разработаны основные понятия математической логики, такие как понятие формулы, аксиомы и правила вывода.

Следующим важным этапом становления математической логики является создание и развитие теории множеств. Теория множеств играла и играет ключевую роль в математике, и ее формализация требовала строгого и ясного логического обоснования. В рамках теории множеств были разработаны такие фундаментальные понятия, как множество, элемент, операции над множествами и отношения между ними.

В последнее время математическая логика стала развиваться в более абстрактном направлении, исследуя логические системы, формализации различных ветвей математики и вычислительные модели. В рамках этого направления были разработаны такие важные теории, как теория моделей, теория доказательств и теория алгоритмов.

• Математическая логика предоставляет математикам исчислительные инструменты и методы для формализации и решения математических задач.
• Она является неотъемлемой частью фундаментальных наук, таких как математика, философия и информатика.
• Развитие математической логики позволило совершить значительные прорывы в различных областях науки и техники, таких как искусственный интеллект, компьютерная наука и криптография.

Таким образом, математическая логика является одной из важнейших и наиболее активно развивающихся областей математики. Ее становление и развитие неразрывно связаны с работой выдающихся математиков и философов, которые стремились установить строгие и ясные правила доказательства и рассуждения.

Первые шаги к математической логике

Первые шаги к математической логике были сделаны еще в V веке до нашей эры древнегреческим математиком и философом Пифагором. Он и его последователи стремились найти логические основания для математических истин, и ввели понятие доказательства.

Однако настоящий прорыв в развитии математической логики произошел в XIX веке. Именно в этот период появилось много новых идей и концепций, которые стали основой для дальнейшего развития логики.

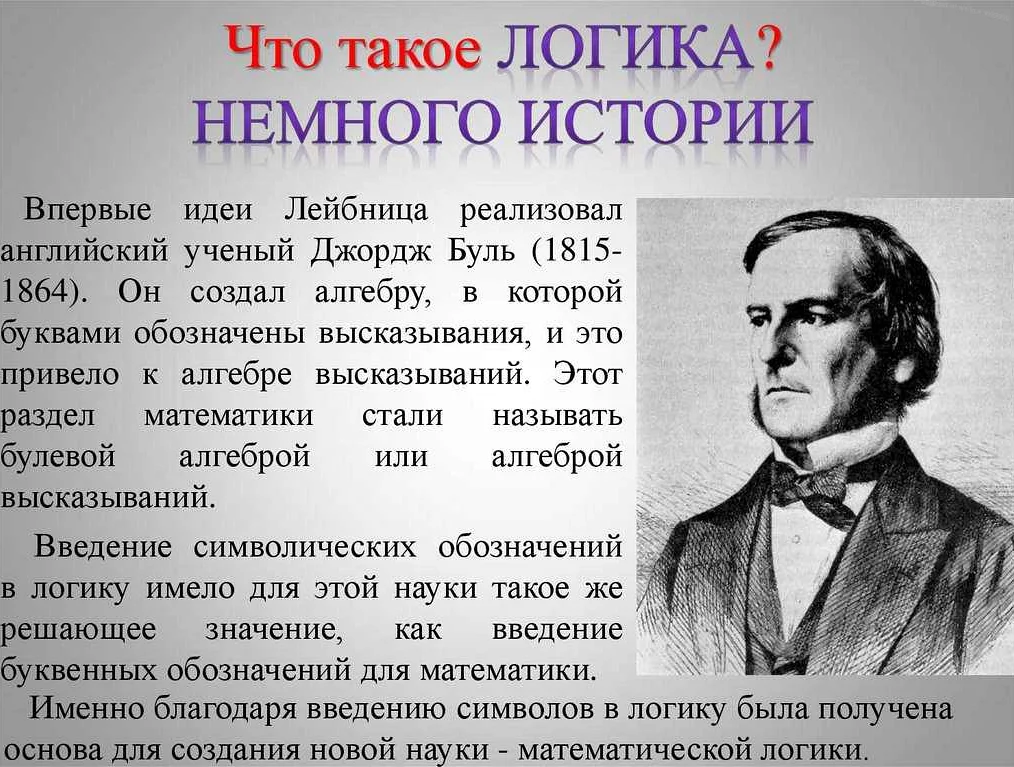
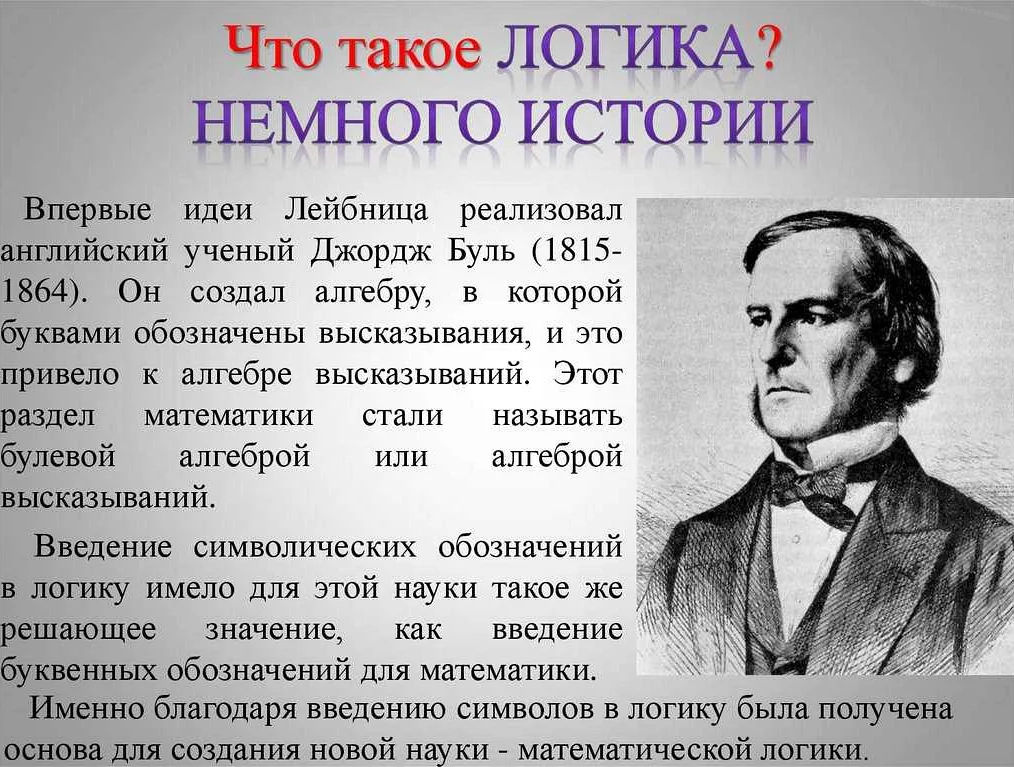
Одним из важнейших вкладов в развитие математической логики была работа Джорджа Буля «Математическая логика, основанная на понятии общности», опубликованная в 1854 году. В этой работе Буль ввел понятие логической алгебры и изложил основные принципы символической логики.

Другим важным вехом в развитии математической логики стало создание аксиоматического метода. Он был разработан математиками Феликсом Клейном и Давидом Гильбертом в конце XIX — начале XX века. Аксиоматический метод заключается в формулировке набора аксиом и правил вывода, на основе которых можно строить доказательства математических теорем.

Таким образом, первые шаги к математической логике были сделаны еще в древние времена, но настоящее развитие этой науки произошло в XIX и XX веках благодаря работе таких ученых, как Пифагор, Джордж Буль, Феликс Клейн и Давид Гильберт.

Жизнь и труды Георга Кантора

Кантор родился в городе Санкт-Петербурге, в семье немецкого происхождения. В 1862 году он поступил в Университет Дорпата (ныне Тартуский университет) в Эстонии, где изучал математику и философию. В 1867 году он получил степень доктора философии за работу по численной теории функций.

В 1874 году Кантор опубликовал свою знаменитую статью «О бесконечных множествах и числах», в которой он впервые представил свою теорию множеств. Он показал, что существует несколько видов бесконечности, и ввел понятие кардинального числа для измерения размерности множеств.

Кантор также занимался исследованием трансфинитных чисел и доказал, что существует бесконечное количество различных кардинальных чисел. Это открытие привело к возникновению понятия «стандартная модель» в математике, которая является основой для изучения бесконечности.

Однако теория множеств Кантора вызвала много споров и критики со стороны его современников математиков. Многие считали его идеи неточными и противоречивыми. Однако со временем теория множеств Кантора получила широкое признание и стала одной из основных теорий в современной математике.

Помимо своих математических исследований, Кантор также занимался педагогической деятельностью. Он преподавал в различных университетах Германии и вел семинары по теории множеств.

В конце жизни Кантор страдал от депрессии и психических расстройств. Он умер в 1918 году в госпитале в городе Хилдесхайме в Германии.

ДатаСобытие

1845	Рождение Георга Кантора в Санкт-Петербурге
1862	Поступление в Университет Дорпата
1867	Получение степени доктора философии
1874	Публикация статьи «О бесконечных множествах и числах»
1918	Смерть Георга Кантора в Хилдесхайме

Математическая логика в работах Джорджа Буля

Джордж Буль был английским математиком и логиком, который внес значительный вклад в развитие математической логики. Он стал известен прежде всего благодаря своей работе «Анализ логического мышления», опубликованной в 1847 году.

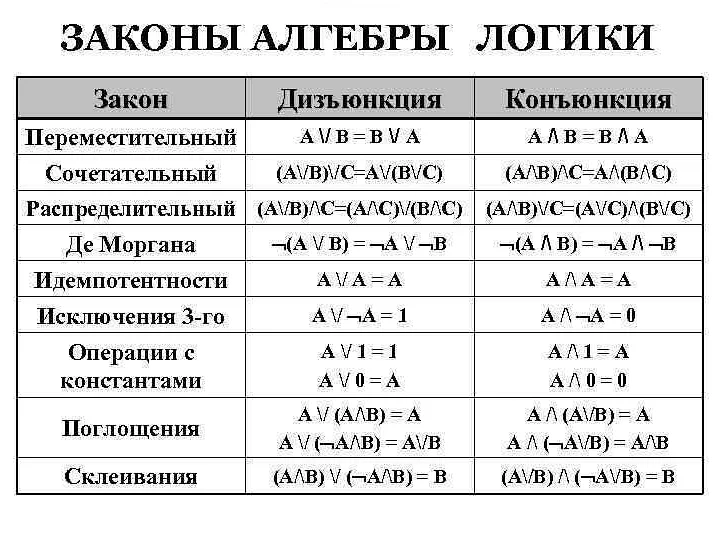
В этой работе Буль представил новый и революционный подход к логике, основанный на алгебре. Он разработал алгебру логики, которая позволяла формализовать логические выражения и операции. Буль ввел такие понятия, как конъюнкция, дизъюнкция и отрицание, и определил операции над ними.

Буль также ввел понятие булевых функций, которые стали основой для создания цифровых компьютеров. Он показал, что булевы функции можно представить с помощью таблиц истинности, и использовал их для анализа и преобразования логических выражений. Эти идеи легли в основу современной дискретной математики и цифровой логики.

Важным вкладом Буля в развитие математической логики стало также его исследование связи между логикой и алгеброй. Он показал, что логические операции можно интерпретировать как операции над множествами, что привело к созданию нового направления в математике — алгебры логики.

Таким образом, работа Джорджа Буля стала важной отправной точкой в развитии математической логики. Его идеи и концепции оказались фундаментальными для создания формальной системы логики и применения ее в различных областях, включая информатику и искусственный интеллект.

Развитие математической логики в трудах Готлоба Фреге

Одной из ключевых идей Фреге была концепция ограниченности математики логической основой. Он разработал идею, что математика должна быть построена на логической основе, и предложил свою систему символов и правил вывода, которые позволяли строить логические доказательства.

Фреге также внес важный вклад в развитие теории множеств. В его работах были сформулированы основные понятия и аксиомы теории множеств, которые стали основой для дальнейшего развития этой области математики. Фреге утверждал, что все математические объекты можно представить в виде множеств и что множества должны иметь однозначные определения и связанные с ними правила.

Однако в 1902 году Фреге столкнулся с парадоксом Рассела, который был основан на его собственной теории множеств. Этот парадокс подверг некоторые из основных идей Фреге сомнению и привел к усилению исследований в области математической логики, чтобы найти новые основы для математики.

Не смотря на парадокс Рассела, вклад Фреге в развитие математической логики остается значительным. Его работы сыграли важную роль в формировании основных принципов и понятий современной математической логики и стали отправной точкой для дальнейшего развития этой области.

Дэвид Гильберт и формализация математики

Дэвид Гильберт, выдающийся немецкий математик, сыграл важную роль в развитии математической логики. Он предложил новое направление в математике, которое называлось «формализацией математики». В своей работе Гильберт стремился создать строгую, формальную систему аксиом и правил вывода, на которой можно было бы построить всю математику. Это был значительный шаг вперед в понимании и развитии математической логики.

Гильберт также предложил концепцию «гильбертовских аксиом», которые были основой для формализации различных математических теорий. Он считал, что эти аксиомы должны быть простыми, ясными и лишеными двусмысленности, чтобы быть надежным фундаментом для всей математики.

Одним из ключевых достижений Гильберта было доказательство теоремы о непротиворечивости арифметики. Это доказательство показало, что в рамках формализации Гильберта невозможно получить противоречивую систему. Оно положило начало новой эпохе в математической логике и способствовало развитию дальнейших исследований в этой области.

Вклад Дэвида Гильберта в формализацию математики и развитие математической логики был огромным. Его работы стали основой для многих последующих исследований и вдохновили многих других ученых заниматься этой областью. Благодаря его трудам мы сегодня имеем строгие математические основы, на которых строится современная наука.

Работы Курта Геделя: основные принципы и теоремы

Одна из наиболее известных работ Геделя — теорема о неполноте. В этой теореме он доказал, что в любой формальной системе, которая достаточно богата для выражения арифметики, существуют истинные утверждения, которые невозможно доказать внутри этой системы. Другими словами, всякую достаточно сложную формальную систему нельзя полностью описать и определить с помощью ее собственных правил.

Еще одной важной работой Геделя является теория множеств и аксиоматика Цермело-Френкеля с аксиомой выбора (ZF). В этой теории Гедель разработал формальный аппарат, позволяющий изучать множества и их свойства с помощью логических методов. Он доказал множество фундаментальных теорем, таких как теорема о непротиворечивости и полноте аксиоматики ZF, а также теорему о континууме.

Также следует отметить работу Геделя над теорией вычислимости. Он ввел понятие рекурсивной функции, которое стало основой для развития компьютерной науки. Гедель доказал ряд важных результатов в этой области, включая его известную теорему о неразрешимости, в которой он показал, что существуют проблемы, которые невозможно решить с помощью механического алгоритма.

Работы Курта Геделя имеют фундаментальное значение для математической логики и ее развития. Они открыли новые горизонты в понимании основ математики и ее формализации. Их влияние ощущается и по сей день, и они остаются неотъемлемой частью истории математики.

Алонзо Чёрч и формальная система лямбда-исчисления

Формальная система лямбда-исчисления основана на идее абстракции и аппликации. В ней функции записываются в виде абстракций, а применение функций к аргументам — в виде аппликации. Чёрч разработал правила для манипулирования функциями, которые были формализованы в виде лямбда-выражений. Лямбда-выражение состоит из параметра, функции и тела, которое определяет, как функция применяется к параметру.

Лямбда-исчисление стало основой для развития теории вычислимости и языков программирования. Эта формальная система позволяет формализовать и изучать понятия вычисления и функций. Она стала основой для создания языков программирования, таких как Lisp, Haskell и других функциональных языков. Чёрч и его работы в области лямбда-исчисления оказали огромное влияние на развитие математической логики и информатики.

Влияние математической логики на развитие информатики и компьютерных наук

Математическая логика, развиваясь в течение многих лет, оказала огромное влияние на развитие информатики и компьютерных наук. Она позволила создать основные принципы и методы, которые лежат в основе современных компьютерных систем и программирования.

Во-первых, математическая логика предоставила фундаментальные инструменты для формализации и описания вычислений. Она помогла в разработке логических систем, которые позволяют формализовать решение задач и алгоритмы, а также проводить доказательства и рассуждения о программных системах. Без математической логики было бы гораздо сложнее разрабатывать и анализировать сложные компьютерные системы.

Во-вторых, математическая логика позволила разработать формальные методы доказательства корректности программ. Она предоставляет инструменты для проверки программ на наличие ошибок и неправильного поведения. Благодаря математической логике, программисты могут создавать компьютерные программы, которые работают предсказуемо и надежно.

В-третьих, математическая логика является основой для разработки языков программирования. Многие языки программирования основаны на математической логике и используют ее концепции и принципы. Благодаря этому, программисты могут использовать эти языки для создания сложных программных систем и алгоритмов.

Таким образом, математическая логика сыграла ключевую роль в развитии информатики и компьютерных наук. Она обеспечила основы для формализации и описания вычислений, разработки формальных методов доказательства корректности программ, а также создания языков программирования. Без математической логики современная информатика и компьютерные науки были бы невозможными.

Вопрос-ответ:

Кто является создателем математической логики?

Математическую логику развивали многие ученые, но ее основными создателями считаются Аристотель, Георг Кантор, Готтлоб Фреге, Давид Гильберт и Курт Гедель.

Какую роль сыграл Аристотель в создании математической логики?

Аристотель является одним из основателей математической логики. Он разработал систему логики, включающую законы исключенного третьего и противоречия, которые до сих пор используются в математике и логике.

Какие идеи предложил Готтлоб Фреге в математической логике?

Фреге предложил идею использования символов и формальных правил для описания математических выражений. Он также разработал теорию множеств, которая стала основой для дальнейшего развития математической логики.

Какие вклады в математическую логику внесли Курт Гедель и Давид Гильберт?

Гедель доказал теорему о неполноте, которая показывает, что существуют утверждения, которые нельзя доказать или опровергнуть в рамках формальной системы. Гильберт же разработал аксиоматический метод, который позволяет изучать математические теории с помощью формальных аксиом и логических законов.

Видео по теме: