Откуда взялся математический термин корень квадратный

Корень квадратный – это математический термин, который описывает операцию извлечения квадратного корня из числа. Узнайте, откуда взялся этот термин и как он используется в математике.

Математический термин «корень квадратный» является одним из основных понятий алгебры. Он используется для обозначения операции, которая позволяет найти число, при возведении которого в квадрат получается данное число. Впервые этот термин был введен в математическую терминологию в Древней Греции.

В Древней Греции математика занимала важное место в образовании и была обязательной частью обучения великих философов. Одним из первых математиков, которые изучали корни квадратные, был Пифагор. Он разработал теорию о числах и открыл, что существуют такие числа, которые не могут быть представлены в виде обыкновенной дроби. Эти числа назвали «иррациональными» и корни из них — «корнями квадратными».

Затем, в Средние века, исследования корней квадратных были продолжены многими математиками, включая Декарта и Ферма. Они разработали методы и формулы для нахождения корней квадратных, которые с течением времени стали основой для современной алгебры.

Таким образом, история происхождения термина «корень квадратный» тесно связана с развитием математики в различные эпохи. Сегодня этот термин широко используется в математических и научных исследованиях, а также в повседневной жизни, где он помогает решать различные задачи и проблемы.

Ранние математические познания

Одной из первых цивилизаций, которая сделала значительный вклад в математику, была Месопотамия. Здесь впервые появились основные математические понятия, такие как числа, операции и измерения. Месопотамские математики использовали систему счисления с основанием 60 и разработали методы для решения уравнений и нахождения неизвестных.

Египетская цивилизация также внесла свой вклад в развитие математики. Египтяне использовали систему счисления с основанием 10 и обладали хорошими навыками в области геометрии. Они использовали геометрические методы для измерения земельных участков и строительства пирамид.

Древнегреческая математика считается одной из самых влиятельных в истории. Древнегреки разработали аксиоматический метод и внесли важный вклад в развитие геометрии. Известные математики, такие как Пифагор, Евклид и Архимед, сформулировали множество математических теорем и законов, которые до сих пор являются основой для изучения математики.

Ранние математические познания стали основой для дальнейшего развития математики и возникновения новых понятий, таких как корень квадратный. Благодаря усилиям этих древних цивилизаций, мы можем понять и использовать математические принципы и методы в нашей повседневной жизни.

Развитие геометрии в Древнем Египте

Египтяне были знамениты своими высоко развитыми знаниями в области математики и геометрии. Они использовали геометрические принципы и методы для строительства пирамид, земледелия и измерения земли.

В Древнем Египте была разработана система измерения площадей и объемов, которая основывалась на геометрических принципах. Эта система была использована для расчетов площадей полей, оценки затрат на строительство и других практических задач.

Одной из самых известных геометрических фигур, использованных в Древнем Египте, был треугольник с прямым углом, известный как «египетский треугольник». Этот треугольник был использован для землеустройства и измерения уровня воды в Ниле.

Древние египтяне также использовали геометрические методы для строительства пирамид. Они использовали прямые линии и перпендикулярные углы, чтобы создать точные и симметричные структуры.

Важным достижением Древнего Египта в области геометрии было развитие методов измерения длин. Они использовали простые геометрические формулы для измерения длин, ширины и высоты различных объектов.

Таким образом, развитие геометрии в Древнем Египте имело огромное значение для практической жизни египтян и оказало влияние на последующие разработки в этой области науки.

Вклад Древней Греции в математику

История математики тесно связана с античными греками, особенно с периодом Древней Греции. В этот период, между VIII и III веками до н.э., греческие математики внесли значительный вклад в развитие математики.

Одним из наиболее известных математиков был Пифагор. Он основал школу, в которой главным принципом было понимание математических отношений через числа. Пифагорейцы открыли много интересных свойств чисел, включая отношения в музыке и геометрические пропорции.

Евклид, также из Древней Греции, известен своим главным трудом «Элементы». Он создал систематическое изложение геометрии, которое оказало огромное влияние на развитие математики. «Элементы» содержат логическое изложение геометрических принципов и доказательства теорем, которые до сих пор изучаются в школах.

Другой знаменитый математик, Архимед, также происходил из Древней Греции. Он сделал значительные открытия в области геометрии, механики и арифметики. Архимед известен своим принципом, который позволяет определить объем тела, погруженного в жидкость, и его законом рычага.

Таким образом, Древняя Греция сыграла важную роль в развитии математики. Многие математические понятия и теории, разработанные греческими математиками, до сих пор используются и изучаются в настоящее время.

Появление алгебры и малые квадратные уравнения

Впервые алгебра как наука возникла в древней Греции и Ближнем Востоке. Однако, понятие корня квадратного как математической операции было известно задолго до этого. Еще в древнем Египте и Вавилоне математики исследовали свойства чисел, в том числе и квадратных корней.

Однако, формализация и систематизация алгебры как науки произошла в работах древнегреческих математиков, в частности, в трудах Эвклида и Архимеда. Они разработали основные правила и методы решения алгебраических уравнений, в том числе и квадратных.

Малые квадратные уравнения – это уравнения вида ax^2 + bx + c = 0, где a, b и c – коэффициенты, причем a ≠ 0. Решение таких уравнений связано с понятием корня квадратного. Если уравнение имеет решение, то его корни можно найти с помощью формулы дискриминанта:

• Если D = b^2 — 4ac > 0, то у уравнения два различных вещественных корня;
• Если D = b^2 — 4ac = 0, то у уравнения есть один вещественный корень;
• Если D = b^2 — 4ac < 0, то у уравнения нет вещественных корней.

Таким образом, развитие алгебры и решение малых квадратных уравнений привели к появлению и формализации понятия «корень квадратный». Этот термин широко используется в математике и находит применение в различных областях науки и техники.

Развитие символики в Средние века

В Средние века символика играла важную роль в математике. Однако, в то время не было стандартных математических символов, которые мы используем в настоящее время. Вместо этого, математики использовали различные символы и обозначения для представления различных математических концепций.

Одним из наиболее известных символов, появившихся в Средние века, был символ квадратного корня. Ранее символы квадратного корня не использовались, и математики обозначали корень квадратный с помощью других символов или слов. Однако, в Средние века был разработан новый символ, который стал обозначать корень квадратный — символ извлечения квадратного корня.

Этот символ представляет собой знак, напоминающий букву «V», с горизонтальной чертой, проходящей через нижнюю часть символа. Однако, этот символ не был широко распространен и использовался только в некоторых рукописях и книгах.

В Средние века также появилась символика для обозначения других математических операций, таких как сложение, вычитание, умножение и деление. Некоторые из этих символов также использовались в настоящее время, хотя и с некоторыми изменениями.

• Символ плюса (+) использовался для обозначения сложения;
• Символ минуса (-) использовался для обозначения вычитания;
• Символ умножения (×) использовался для обозначения умножения;
• Символ деления (÷) использовался для обозначения деления.

Эти символы были разработаны для того, чтобы облегчить запись математических операций и сделать их более легкими для понимания. Они были широко использованы в Средние века и стали основой для развития современной математической символики.

Термин «корень квадратный» в математике

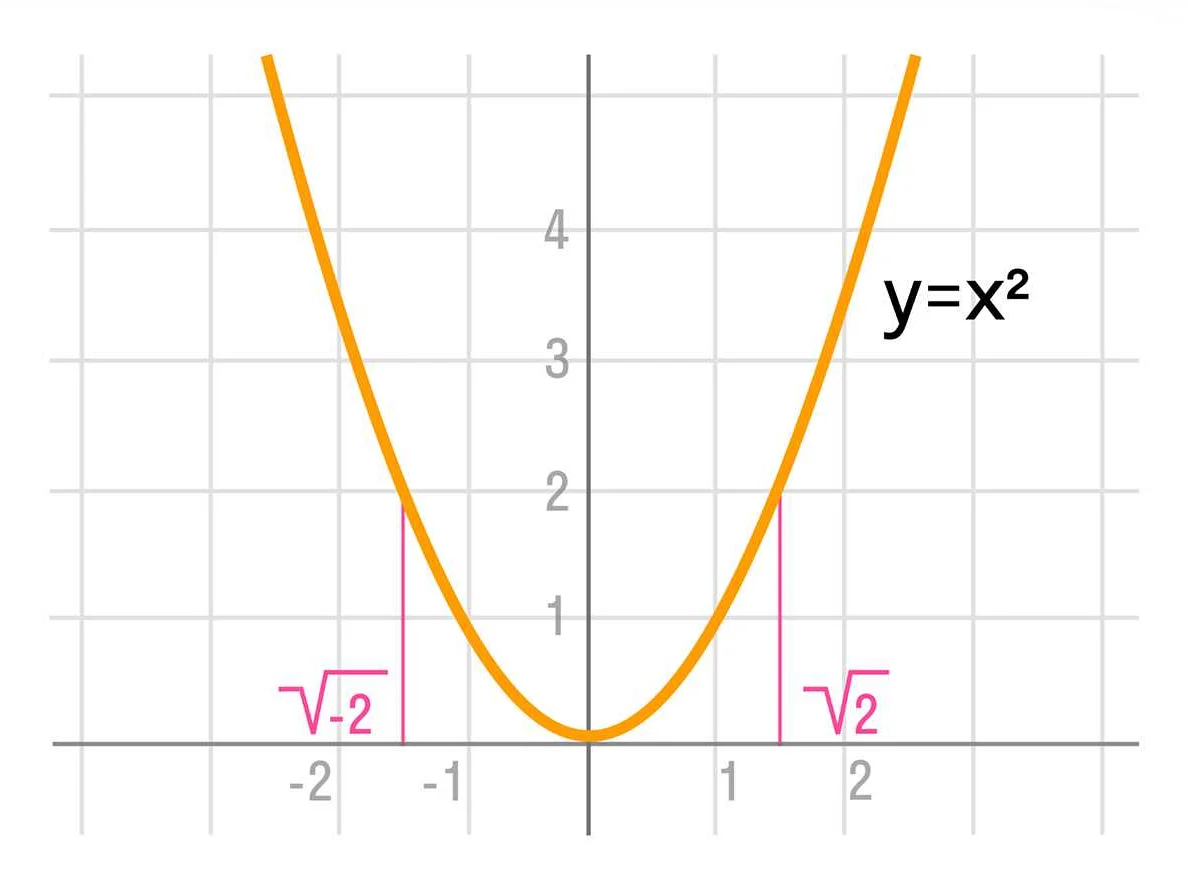
Корень квадратный обозначается символом √ и записывается перед выражением, подкоренным числом. Например, корень квадратный из числа 9 обозначается как √9 и равен 3, так как 3 √3 = 9.

История происхождения термина «корень квадратный» связана с развитием математики в Древней Греции. В Древней Греции многие математики, такие как Пифагор, были заинтересованы в изучении чисел и их свойств. Они заметили, что некоторые числа могут быть представлены в виде квадратов других чисел.

Например, число 9 можно представить как квадрат числа 3, так как 3 √3 = 9. Эта идея впоследствии привела к развитию понятия «корень квадратный».

С течением времени математики стали изучать корни квадратные разных чисел и разрабатывать методы для их вычисления. Они также обнаружили, что некоторые числа не имеют рациональных корней квадратных, что привело к развитию понятия «иррациональных чисел».

Сегодня корень квадратный широко используется в различных областях математики и науки. Он является одним из основных понятий алгебры и используется для решения уравнений, нахождения длины сторон прямоугольного треугольника и в других задачах.

Применение корня квадратного в реальной жизни

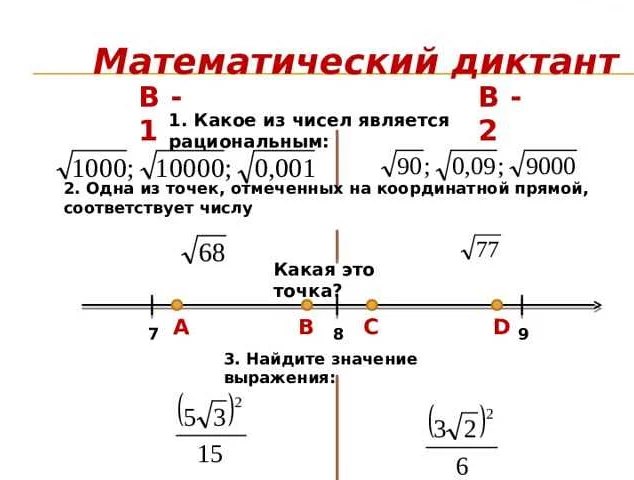
Одно из основных применений корня квадратного — это вычисление длины стороны квадрата или прямоугольника, если известна площадь. Например, если у нас есть квадрат со площадью 25 квадратных метров, то мы можем использовать корень квадратный, чтобы найти длину его стороны. В данном случае корень квадратный из 25 равен 5, так что сторона квадрата будет равна 5 метрам.

Корень квадратный также используется для решения задач, связанных с движением и скоростью. Например, если мы знаем скорость объекта и время, которое он двигался, мы можем использовать корень квадратный, чтобы найти расстояние, которое он прошел. Формула для вычисления расстояния при равномерном движении имеет вид: расстояние = скорость * время. Если мы знаем скорость и время, то можем использовать корень квадратный, чтобы найти расстояние.

Корень квадратный также применяется в геометрии для нахождения длины диагонали квадрата или прямоугольника. Если мы знаем длину стороны, то можем использовать корень квадратный, чтобы найти длину диагонали. Например, если сторона квадрата равна 3 метрам, то длина диагонали будет равна корню квадратному из 3^2 + 3^2 = 9 + 9 = 18. Таким образом, длина диагонали будет равна корню квадратному из 18.

В общем, корень квадратный — это очень полезная математическая операция, которая находит широкое применение в реальной жизни. Он помогает решать различные задачи, связанные с измерениями, движением и геометрией. Благодаря корню квадратному мы можем точно вычислять и измерять различные величины и применять их в практических задачах.

Вопрос-ответ:

Каково происхождение математического термина «корень квадратный»?

Термин «корень квадратный» происходит от латинского слова «radix», что означает «корень». В математике он используется для обозначения операции извлечения квадратного корня числа.

Кто ввел в математику термин «корень квадратный»?

Введение термина «корень квадратный» в математику связывают с работами арабского математика Абу Камиля Аль-Хорезми в IX веке. Он активно развивал алгебру и ввел в нее такие понятия, как квадратный корень и его извлечение.

Какие другие термины связаны с понятием «корень квадратный»?

В математике также используются понятия «корень» и «корень n-ной степени». Корень — это обратная операция к возведению в степень. Корень n-ной степени позволяет извлекать корни любой степени из числа.

Как корень квадратный связан с геометрией?

Корень квадратный тесно связан с понятием квадрата и его площади. Если известна площадь квадрата, то корень квадратный этой площади даст длину стороны квадрата. Это позволяет решать задачи геометрии, связанные с квадратами и их площадями.

Какие применения имеет корень квадратный в реальной жизни?

Корень квадратный находит применение во многих областях жизни. Например, он используется в физике для решения задач, связанных с движением и силой. Также корень квадратный применяется в статистике для расчета среднего отклонения и дисперсии.

Какой математический термин имеет историю происхождения?

Математический термин, имеющий интересную историю происхождения, — «корень квадратный».

Откуда происходит термин «корень квадратный»?

Термин «корень квадратный» происходит из латинского слова «radix», что означает «корень».

Современное использование и понимание термина «корень квадратный»

Сегодня термин «корень квадратный» широко используется в математике и связанных с ней дисциплинах. Он относится к операции, обратной возведению в квадрат. Корень квадратный позволяет найти число, при возведении которого в квадрат получается заданное число.

В математическом обозначении корень квадратный обычно записывается символом √x, где x — число, из которого извлекается корень. Так, корень квадратный из числа 4 обозначается как √4 и равен 2, так как 2^2 = 4.

Корень квадратный имеет много применений в различных областях науки и техники. Например, он используется при решении уравнений, моделировании физических процессов, анализе данных и создании компьютерных алгоритмов.

Кроме того, понимание термина «корень квадратный» позволяет лучше понять и оценить различные математические концепции, такие как понятие квадратного уравнения, теорема Пифагора и теория вероятностей.

Таким образом, современное использование и понимание термина «корень квадратный» является важным элементом в изучении математики и ее применении в реальном мире.

Видео по теме: