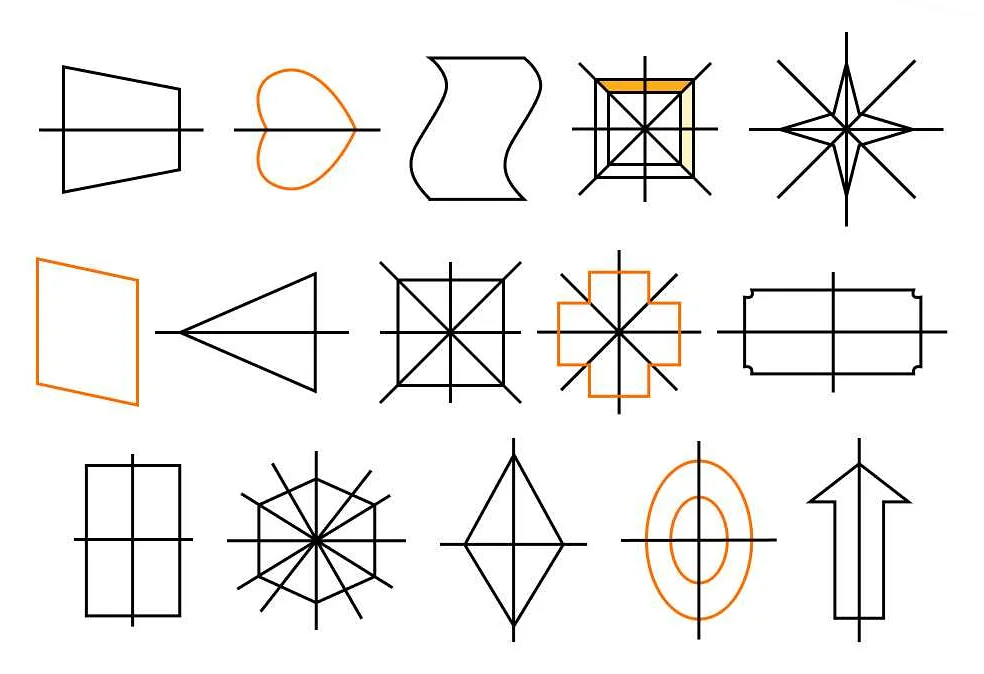Кто придумал симметрию в математике

Статья рассказывает о том, кто придумал и изучает симметрию в математике, ее роль в различных областях и приложениях, а также о важных понятиях и принципах, связанных с симметрией.

Симметрия – это одно из основных понятий в математике, которое широко применяется в различных областях науки, искусства и дизайна. Возникновение и развитие этого понятия можно проследить на протяжении долгой истории человечества.

Первые упоминания о симметрии находятся в древних греческих текстах. Великий ученый Архимед, работающий в III веке до нашей эры, проводил исследования в области симметрии и описывал ее в своих работах. Архимед понимал симметрию как равенство относительно данной прямой – оси симметрии. Это понятие стало основой для дальнейших исследований и развития симметричных структур.

В средние века исследование симметрии продолжилось и вошло в сферу интересов арабских математиков. Они активно изучали симметричные фигуры и разработали методы для их изучения и классификации. Одним из ключевых моментов в развитии симметрии в этот период было открытие пяти основных симметричных групп, которые состоят из различных элементов и операций симметрии.

С развитием науки и математики симметрия стала неотъемлемой частью многих областей знания. Современные исследования в этой области позволяют применять симметрию в различных научных и практических задачах, а также использовать ее в графике и дизайне для создания гармоничных и привлекательных образов.

В конце XX века симметрия стала активно изучаться и применяться в физике, особенно в теории элементарных частиц и квантовой механике. Ученые обнаружили, что симметрия является одним из основных принципов, определяющих фундаментальные законы природы. Исследования в этой области продолжаются и приводят к новым открытиям и пониманию сущности симметрии.

Возникновение симметрии в математике

Идея симметрии имеет древние корни и пронизывает различные области человеческой деятельности. В математике концепция симметрии стала объектом исследования с древних времен и пережила множество развитий и совершенствований.

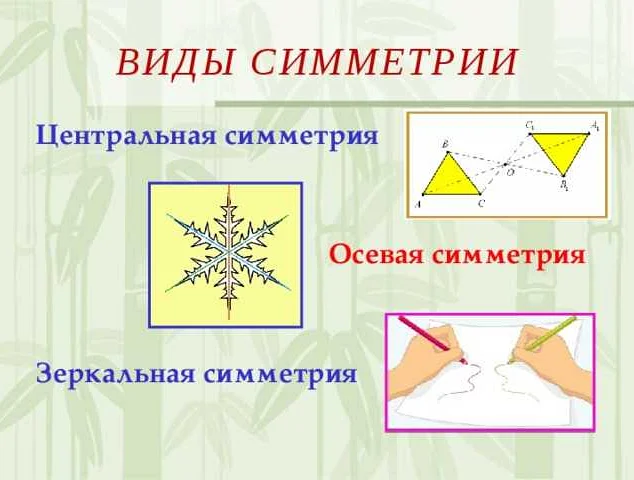
Первые шаги в изучении симметрии были сделаны греческими учеными, такими как Архимед и Евклид. Они обратили внимание на особенности геометрических фигур и определили различные виды симметрии, такие как осевая симметрия и центральная симметрия.

В последующие века математики продолжали изучать симметрию и разрабатывать новые методы ее анализа. Важным вкладом в развитие теории симметрии стала работа немецкого математика Феликса Клейна в конце XIX — начале XX века. Он разработал систематический подход к изучению симметрии и формализовал ее определение.

Сегодня симметрия играет важную роль в различных областях математики, таких как геометрия, алгебра и теория групп. Она используется для решения различных задач, а также имеет важное значение в современных исследованиях, связанных с физикой и кристаллографией.

• Симметрия помогает упростить сложные задачи и найти эффективные решения.
• Она позволяет классифицировать объекты и выявлять их общие характеристики.
• Симметрия находит применение в дизайне, искусстве и архитектуре, придавая им гармоничность и красоту.

Исследования симметрии продолжаются и современные математики работают над дальнейшим расширением ее теории и применениями в различных областях знания.

Видео по теме:

Архимед и его вклад в развитие симметрии

Архимед, древнегреческий математик, физик, инженер и изобретатель, сыграл значительную роль в развитии симметрии. Его работы и открытия в области математики и физики имели важное значение не только для его собственного времени, но и для последующих поколений ученых.

Одним из важных вкладов Архимеда в развитие симметрии было его использование метода исчисления пределов для вычисления площадей и объемов фигур. Он разработал метод, который позволял приближенно вычислять площадь криволинейных фигур, таких как параболы и спирали, приближая их многоугольниками. Этот метод, известный как метод «исчисления величин бесконечно малых», был предтечей интегрального исчисления и имеет прямое отношение к симметрии.

Архимед также был автором теоремы об известном как «вертушка Архимеда», которая описывает свойства определенного класса кривых. Эта теорема основана на симметрии и позволяет вычислить длину кривой при помощи геометрических методов.

Кроме того, Архимед занимался исследованием симметрии в области механики. Он был первым, кто сформулировал принцип равенства давлений в жидкостях, который известен как «закон Архимеда». Этот принцип основан на симметрии: если на тело, погруженное в жидкость, действуют силы только с одной стороны, то оно будет испытывать поднимающую силу, равную весу вытесненной жидкости.

В целом, вклад Архимеда в развитие симметрии был огромным. Его работы и открытия в области математики и физики сыграли важную роль в формировании основ науки и вдохновили многих ученых последующих времен.

Симметрия в геометрии и ее открытие в Древнем Египте

В Древнем Египте симметрия использовалась в архитектуре, искусстве и религии. Египтяне строили свои храмы, пирамиды и другие сооружения с использованием симметричных форм. Они верили, что симметричность отражает гармонию и космический порядок.

При изучении древнеегипетских иероглифов и исследовании их симметричной природы можно увидеть, что египтяне использовали ось симметрии для создания баланса и гармонии в своих символах.

Одним из наиболее известных примеров использования симметрии в древнеегипетской архитектуре является Пирамида Хеопса. Ее форма является симметричной относительно вертикальной оси, что создает впечатление монументальности и величия.

Древнеегипетская симметрия также проявлялась в искусстве, особенно в изображениях богов и фараонов. Эти изображения были созданы с использованием симметричных форм и узоров, чтобы подчеркнуть важность и величие древнеегипетской власти и божественности.

В целом, открытие и использование симметрии в геометрии Древним Египтом играло значительную роль в развитии математики и искусства. Это позволило древним египтянам создавать сложные и эстетически привлекательные сооружения и произведения искусства.

Развитие симметрии в средние века и Возрождение

В средние века и эпоху Возрождения, интерес к симметрии в математике продолжал расти. Некоторые ученые и художники начали изучать и использовать симметричные формы в своих работах.

Одним из самых известных примеров симметрии в этот период является использование геометрической симметрии в архитектуре соборов и замков. Архитекторы старались создать симметричные и гармоничные структуры, чтобы усилить эстетическое впечатление.

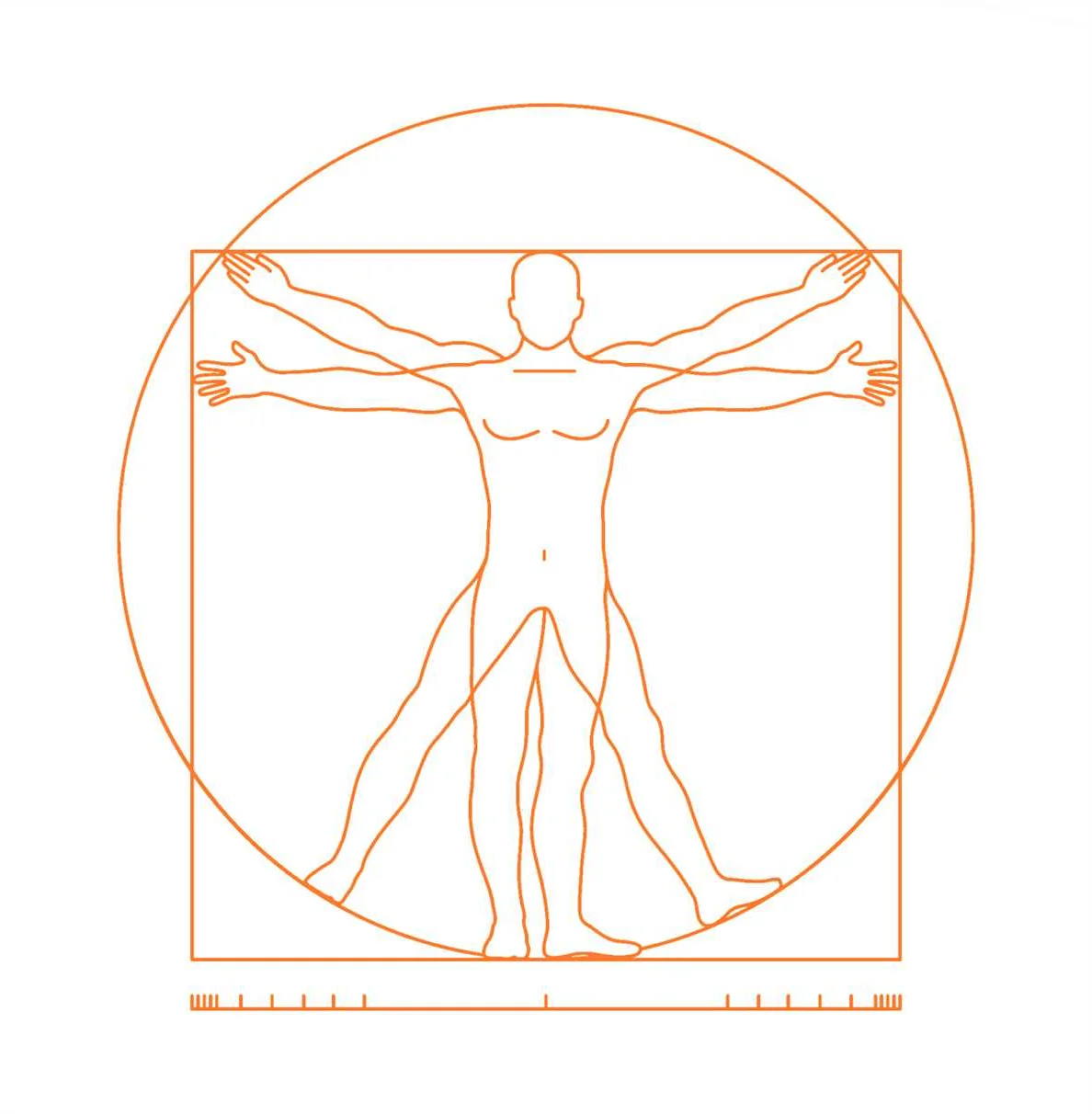
В течение Возрождения, симметрия стала важным элементом в живописи и скульптуре. Художники использовали симметрию, чтобы создавать баланс и гармонию в своих произведениях. Одним из самых известных примеров является Витрувианский человек Леонардо да Винчи, который иллюстрирует идеалы пропорции и симметрии в человеческом теле.

В математике также продолжались исследования симметрии. Одной из важных открытий было открытие симметрии в геометрии, которое стало основой для развития евклидовой геометрии. Математики начали изучать симметричные фигуры, такие как треугольники и круги, и разрабатывать правила для работы с ними.

Таким образом, в средние века и эпоху Возрождения симметрия продолжала развиваться как важный элемент в архитектуре, искусстве и математике. Это был период, когда интерес к симметрии стал все более ярко выраженным и симметричные формы стали неотъемлемой частью культурного наследия этого времени.

Открытие симметрии в алгебре и анализе

Одним из первых, кто заметил симметричность в алгебре, был Франц Абеля. Он разработал теорию групп, которая описывает симметричность в алгебре. В своих работах Абель показал, что существуют различные типы групп и что симметрия может быть представлена в виде операций над элементами множества.

Другой важной фигурой в открытии симметрии в алгебре был Нильс Генрик Абел. Абел разработал теорию абелевых групп, которые являются особым типом групп и имеют определенные свойства симметрии. Он показал, что существуют группы, в которых можно выполнять операции коммутации, что является формой симметрии.

В анализе понятие симметрии также нашло свое применение. Одним из основоположников анализа и теории функций был Леонард Эйлер. Он заметил, что многие функции обладают определенными симметричными свойствами. Это позволило ему разработать методы и техники решения дифференциальных уравнений и изучения функций с помощью симметрии.

Симметрия в алгебре и анализе играет важную роль не только в теоретическом плане, но и в практическом применении. Она позволяет упростить вычисления, найти решения уравнений и понять свойства функций. Благодаря открытию симметрии в алгебре и анализе математики смогли разработать новые методы и инструменты для решения сложных задач и улучшения нашего понимания мира.

Симметрия в современной математике и ее роль в современных исследованиях

Симметрия позволяет упростить проблемы и задачи, связанные с анализом и предсказанием поведения объектов и систем. Она позволяет выявить закономерности и установить связи между различными аспектами математического объекта или модели.

В современной математике симметрия используется в различных областях исследований, таких как алгебра, геометрия, теория чисел, математическая физика и др. Симметричные структуры и операции позволяют решать сложные задачи, создавать новые математические модели и теории, а также разрабатывать алгоритмы для вычислений и анализа данных.

Одной из основных областей исследований, где симметрия играет важную роль, является теория групп. Группы симметрий являются основой для изучения абстрактных симметрийных структур и их применения в различных областях математики и физики.

Симметрия также применяется в компьютерных науках, искусственном интеллекте и машинном обучении. Алгоритмы симметрии используются для оптимизации и ускорения вычислений, а также для решения задач распознавания образов, классификации данных и др.

Область исследованияРоль симметрии

Алгебра	Изучение групп симметрий и абстрактных симметричных структур
Геометрия	Анализ и построение симметричных фигур и пространств
Теория чисел	Изучение симметричных свойств чисел и их последовательностей
Математическая физика	Применение симметрии для решения уравнений и моделирования физических систем
Компьютерные науки	Использование алгоритмов симметрии для оптимизации вычислений и анализа данных

Таким образом, симметрия в современной математике является неотъемлемой частью исследований в различных областях. Она позволяет упростить задачи, выявить закономерности и создать новые математические модели и теории. Симметричные структуры и операции также играют важную роль в разработке алгоритмов и методов анализа данных, что делает симметрию не только интересным математическим концептом, но и практически полезным инструментом для решения реальных проблем.

Применение симметрии в физике и других науках

Одним из наиболее известных примеров применения симметрии в физике является использование группы симметрии для описания физических систем. Группа симметрии — это математический объект, который характеризует набор всех преобразований, сохраняющих форму и свойства системы. Например, группа симметрии может описывать преобразования, сохраняющие законы сохранения энергии, импульса или момента.

Концепция симметрии также находит применение в теории поля и теории элементарных частиц. В современной физике симметрия играет важную роль в построении моделей физических взаимодействий и предсказании новых физических явлений. Например, симметрия Лоренца используется в теории относительности для описания пространственно-временной симметрии физических законов.

Симметрия также применяется в химии для описания молекулярной структуры и химических свойств веществ. Механизмы химических реакций и взаимодействий молекул могут быть объяснены с помощью симметричных принципов.

В биологии симметрия играет важную роль в понимании структуры и функции организмов. Биологические системы, такие как органы, клетки и гены, обладают симметричной организацией, которая определяет их форму и функцию.

В математике симметрия изучается в различных областях, включая геометрию, алгебру и теорию групп. Математические методы и концепции симметрии находят применение во многих науках, помогая упростить и объяснить сложные явления и законы природы.

В заключение, применение симметрии в физике и других науках является мощным инструментом для понимания природы и построения моделей, позволяющих предсказывать и объяснять различные явления. Изучение симметрии продолжает быть одной из активных областей исследований и вносит значительный вклад в развитие науки и технологий.

Вопрос-ответ:

Какие исторические факты способствовали возникновению концепции симметрии в математике?

Возникновение концепции симметрии в математике было обусловлено несколькими историческими факторами. Одним из них была работа Архимеда, который в своих исследованиях использовал симметричные формы и отношения. Ещё одним фактором были исследования египетских математиков, которые также использовали симметрию в своей работе. Важным вехой стало открытие группы симметрии окружности, которое сделал Пафнутий Чебышёв в 1871 году.

Как симметрия применяется в современных математических исследованиях?

Симметрия играет важную роль в современных математических исследованиях. Она используется в различных областях, таких как геометрия, алгебра, теория чисел и топология. Например, симметричные алгебраические структуры, такие как группы и кольца, являются основой абстрактной алгебры. Симметричные объекты и преобразования также используются для решения различных задач в физике, химии и биологии.

Какие вклады в исследование симметрии внесли математики в разные эпохи?

Математики разных эпох внесли значительные вклады в исследование симметрии. В Древней Греции Архимед использовал симметрию в своих исследованиях и доказательствах. В средние века учёные изучали симметрию в геометрии и алгебре. В новое время Пафнутий Чебышёв разработал теорию симметрии функций и внёс важный вклад в развитие математики. Современные математики продолжают исследование симметрии и применяют её в различных областях математики и наук.

Какие великие математики внесли вклад в исследование симметрии?

В исследование симметрии в математике внесли вклад множество великих умов. Некоторые из них: Архимед, Евклид, Леонардо Пизанский (Фибоначчи), Карл Фридрих Гаусс, Эмиль Эртель, Феликс Клейн, Георг Кантор, Эмиль Артин, Хари Шандер, Андрей Колмогоров, Александр Гротендик.

Какая роль симметрии в математике?

Симметрия играет важную роль в математике. Она помогает упростить и классифицировать объекты, а также найти закономерности и общие свойства. Симметричные фигуры и структуры также имеют эстетическое значение и широко используются в различных областях, включая геометрию, алгебру, теорию чисел и фракталы.

Какие приложения симметрии существуют в современном мире?

Симметрия имеет множество приложений в современном мире. Некоторые из них включают дизайн и архитектуру, кристаллографию, компьютерную графику, криптографию, физику и химию. Например, симметричные кристаллические структуры используются в разработке новых материалов, а симметрия в компьютерной графике помогает создавать реалистичные визуальные эффекты и анимацию.