Производные математика как решать
Содержимое
- 1 Производные математика как решать
- 1.1 Определение производной функции
- 1.2 Правила дифференцирования функций
- 1.3 Применение производных в решении задач
- 1.4 Найти экстремумы функции с помощью производной
- 1.5 Определение скорости изменения функции с помощью производной
- 1.6 Найти точку перегиба функции с помощью второй производной
- 1.7 Использование производных в оптимизационных задачах
- 1.8 Применение производных в физических задачах
- 1.9 Видео по теме:
Узнайте, как решать производные в математике с помощью простых шагов и правил. Научитесь находить производные функций и использовать их для решения различных задач. Познакомьтесь с основными понятиями и методами производных и улучшите свои навыки в математике.
Производные являются одним из основных инструментов математического анализа и нахождения экстремумов функций. Решение задач с производными позволяет найти максимумы и минимумы функций, а также определить их поведение в разных точках. Это важный инструмент для оптимизации, поэтому знание производных является неотъемлемой частью обучения математике и физике.
Для решения задач с производными необходимо знать основные правила дифференцирования. Они позволяют находить производные различных функций, включая композиции функций, суммы и произведения. Знание этих правил облегчает процесс решения задач с производными и позволяет более точно анализировать функции.
Например, для нахождения экстремумов функции необходимо найти точки, в которых первая производная равна нулю или не существует, а затем анализировать значение второй производной в этих точках. Если вторая производная положительна, то это точка минимума, а если отрицательна, то это точка максимума.
Кроме того, для решения задач с производными можно использовать геометрический подход. Например, график функции и ее производной могут помочь визуализировать поведение функции и найти точки экстремума. Также можно использовать график для определения оптимальных значений переменных в задачах оптимизации.
Основной секрет решения задач с производными — это практика. Чем больше задач вы решаете, тем лучше вы понимаете применение производных и получаете навыки решения сложных задач. Не бойтесь экспериментировать с различными методами решения и постоянно углублять свои знания в области производных.
Определение производной функции

Формально, производная функции f(x) в точке x₀ определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю:
$$f'(x₀) = \lim_{{\Delta x \to 0}} \frac{{f(x₀ + \Delta x) — f(x₀)}}{{\Delta x}}$$
Если данный предел существует, то функция является дифференцируемой в точке x₀, а значение этого предела и будет являться производной функции в этой точке.
Интуитивно можно представить производную функции как скорость изменения значения функции в данной точке. Если производная положительна, то функция возрастает в данной точке, если отрицательна — убывает, а если равна нулю — функция имеет экстремум в этой точке.
Производная функции позволяет решать множество задач, таких как определение точек экстремума, нахождение касательной к графику функции, исследование функций на монотонность и выпуклость, а также решение уравнений и неравенств с использованием производных.
Правила дифференцирования функций
Правило линейности: Если функция f(x) является линейной комбинацией двух других функций u(x) и v(x), то её производная равна линейной комбинации производных этих функций:
f'(x) = ku'(x) + lv'(x),
где k и l — константы.
Правило сложной функции: Если функция f(x) является композицией двух других функций u(x) и v(x), то её производная может быть найдена с помощью цепного правила:
f'(x) = u'(v(x)) * v'(x).
Правило степенной функции: Если функция f(x) является степенной функцией вида f(x) = x^n, где n — константа, то её производная равна:
f'(x) = n * x^(n-1).
Это правило называется также правилом производной степени.
Правило суммы и разности функций: Если функции f(x) и g(x) имеют производные f'(x) и g'(x), то производная их суммы f(x) + g(x) равна сумме их производных:
(f+g)'(x) = f'(x) + g'(x).
Аналогично, производная разности f(x) — g(x) равна разности их производных:
(f-g)'(x) = f'(x) — g'(x).
Эти правила дифференцирования позволяют упростить процесс нахождения производной функции и использовать его для решения задач различной сложности.
Применение производных в решении задач

Производные могут быть использованы для определения скорости изменения функции в конкретной точке. Например, если у нас есть функция, описывающая движение объекта в пространстве, то производная этой функции позволит нам определить скорость объекта в любой момент времени. Это особенно полезно при решении задач физики и механики.
Кроме того, производные позволяют находить экстремумы функций, то есть точки, где функция достигает своего максимума или минимума. Это может быть полезно при оптимизации процессов, например, при нахождении оптимального времени или объема для выпуска продукции.
Еще одним применением производных является нахождение точек перегиба функций. Точка перегиба — это точка, в которой функция меняет свой тип выпуклости или вогнутости. Это может быть полезно при исследовании формы кривых, например, при анализе графика функции или построении математических моделей.
В целом, производные играют ключевую роль в анализе функций и находят применение во многих областях науки и техники. Знание и умение применять производные позволяет решать сложные задачи и делать более точные и эффективные расчеты.
Найти экстремумы функции с помощью производной
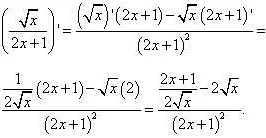
Для начала необходимо найти производную функции. Производная функции показывает, как изменяется функция при изменении ее аргумента. Если производная равна нулю в некоторой точке, то это может быть точка экстремума.
Для нахождения экстремумов функции следует выполнить следующие шаги:
- Найти производную функции.
- Найти все точки, в которых производная равна нулю или не существует. Эти точки могут быть точками экстремума.
- Проверить значения функции в найденных точках. Если значение функции в точке, где производная равна нулю, больше значений функции в соседних точках, то это точка минимума. Если значение функции в точке, где производная равна нулю, меньше значений функции в соседних точках, то это точка максимума.
Если производная функции равна нулю в нескольких точках, то можно взять вторую производную и проверить ее знак в этих точках. Если вторая производная положительна, то это точка минимума, если отрицательна, то это точка максимума.
Применение производной для нахождения экстремумов функции является эффективным и универсальным методом. Однако, следует помнить, что производная может равняться нулю и в других точках, которые не являются экстремумами, поэтому необходимо проводить дополнительные проверки.
ПримерИсходная функцияПроизводная функцииТочки экстремумаВид экстремума
| 1 | f(x) = x^2 | f'(x) = 2x | x = 0 | минимум |
| 2 | f(x) = x^3 | f'(x) = 3x^2 | x = 0 | точка перегиба |
| 3 | f(x) = sin(x) | f'(x) = cos(x) | x = (2n + 1) * pi/2, где n — целое число | точки максимума и минимума |
Определение скорости изменения функции с помощью производной
Скорость изменения функции в конкретной точке определяется как значение производной функции в этой точке. Производная функции в точке является пределом отношения изменения значения функции к изменению аргумента при стремлении изменения аргумента к нулю.
Производная функции позволяет определить, как быстро изменяется функция в каждой точке ее области определения. Если производная функции положительна, то функция возрастает в данной точке, то есть ее значения увеличиваются при увеличении аргумента. Если производная функции отрицательна, то функция убывает в данной точке, то есть ее значения уменьшаются при увеличении аргумента.
Производная также может быть равна нулю в некоторых точках функции. В этом случае говорят, что функция имеет экстремум в данной точке. Если производная меняет знак с минуса на плюс, то функция имеет локальный минимум. Если производная меняет знак с плюса на минус, то функция имеет локальный максимум.
Определение скорости изменения функции с помощью производной позволяет решать множество задач в различных областях науки и техники. Например, оно может быть использовано для определения максимальной прибыли в экономике, максимальной скорости движения тела в физике, оптимального времени доставки груза в логистике и т.д.
Важно знать, что производная функции определена не для всех функций. Некоторые функции могут не иметь производной в некоторых точках или вообще не иметь производной. Поэтому перед применением производной необходимо убедиться в ее существовании.
Найти точку перегиба функции с помощью второй производной
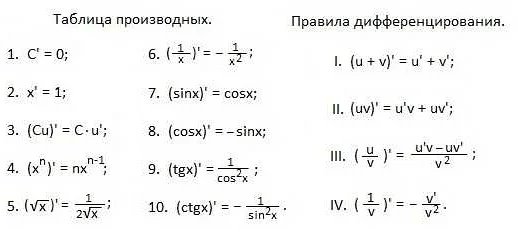
Для того чтобы найти точку перегиба функции, нужно выполнить следующие шаги:
- Найти вторую производную функции.
- Решить уравнение второй производной равное нулю. Полученные значения x будут являться координатами точек перегиба.
- Определить характер перегиба в каждой найденной точке, используя знак второй производной. Если вторая производная больше нуля, то функция выпукла в этой точке. Если вторая производная меньше нуля, то функция вогнута в этой точке.
Зная координаты точек перегиба и их характер, можно построить график функции с учетом этих особенностей.
Таким образом, использование второй производной позволяет найти точки перегиба функции и определить их характер, что является важным инструментом при анализе графиков функций и решении задач в математике.
Использование производных в оптимизационных задачах
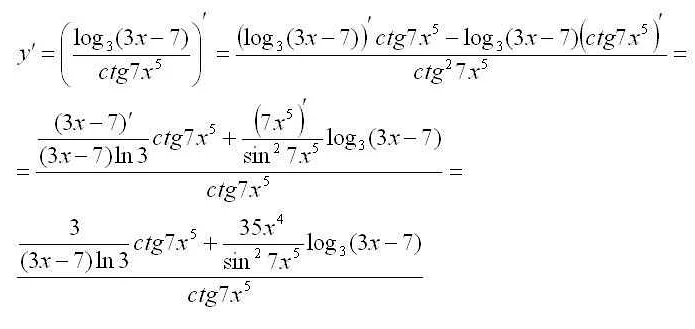
Для решения оптимизационной задачи с использованием производной, нужно сначала найти производную заданной функции. Затем исследуется поведение производной в различных точках, чтобы найти точки, где производная равна нулю или не существует. Эти точки могут представлять максимум или минимум функции.
Далее, чтобы определить, является ли найденная точка экстремумом, необходимо проанализировать знак производной в окрестности этой точки. Если производная меняет знак с плюса на минус, то мы имеем локальный максимум. Если производная меняет знак с минуса на плюс, то мы имеем локальный минимум.
Оптимизационные задачи с производными встречаются в различных областях науки и инженерии. Они могут быть использованы для оптимизации производства, финансовых моделей, научных исследований и многих других областей. Важно уметь правильно применять производные для решения таких задач.
Применение производных в физических задачах
В механике, производные применяются для нахождения скорости и ускорения тела. Например, скорость – это производная от перемещения по времени, а ускорение – производная от скорости. Зная уравнение движения тела, можно использовать производные для определения моментов, когда скорость или ускорение достигают максимальных или минимальных значений.
В электродинамике, производные используются для описания изменения электрического поля и магнитного потока. Например, в законе Фарадея и законе Гаусса для электромагнитной индукции, производные позволяют определить электродвижущую силу и силовую линию электрического поля.
Производные также применяются в оптике для описания изменения интенсивности света при прохождении через различные среды и преломлении. Например, закон Снеллиуса, который описывает отклонение светового луча при переходе из одной среды в другую, содержит производные для определения угла преломления.
Использование производных в физических задачах позволяет более точно описывать и предсказывать различные явления и процессы в природе. Это один из основных инструментов математического анализа, который находит широкое применение в физике, как теоретической, так и экспериментальной.
Видео по теме:
Какие есть основные правила для решения задач с производными?
Для решения задач с производными существуют несколько основных правил. Во-первых, есть правило линейности, которое гласит, что производная суммы двух функций равна сумме производных этих функций. Во-вторых, есть правило произведения, которое утверждает, что производная произведения двух функций равна произведению производной первой функции на вторую функцию, плюс произведение первой функции на производную второй функции. В-третьих, есть правило частного, которое указывает, что производная частного двух функций равна разности произведения производной первой функции на вторую функцию и произведения первой функции на производную второй функции, деленной на квадрат второй функции. Еще есть правило степенной функции, правило экспоненты и правило логарифма.
Как найти производную функции?
Чтобы найти производную функции, нужно применить правила дифференцирования. Возьмем функцию f(x). Если функция представлена в виде суммы или разности других функций, то для нахождения производной можно использовать правило линейности. Если функция представлена в виде произведения двух функций, то для нахождения производной можно использовать правило произведения. Если функция представлена в виде частного двух функций, то для нахождения производной можно использовать правило частного. Если функция представлена в виде степенной функции, экспоненты или логарифма, то для нахождения производной можно использовать соответствующие правила. Применяя эти правила, можно пошагово находить производную функции.
Какие есть практические примеры решения задач с производными?
Применение производных можно встретить во многих областях. Например, в физике для нахождения скорости или ускорения объекта. В экономике для определения максимального прибытка или минимальных издержек. В медицине для определения наиболее эффективного лечения. В инженерии для нахождения оптимальных параметров конструкции. В зависимости от конкретной задачи, применение производных может быть разным, но общий принцип решения остается неизменным — нахождение производной функции и анализ ее свойств.

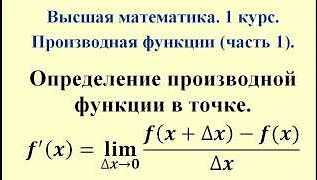

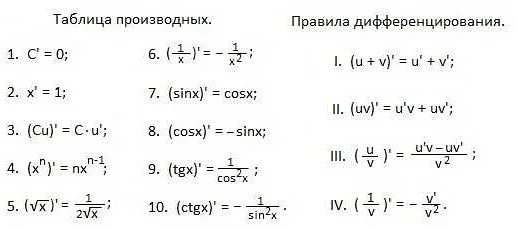

Статья очень полезная и информативная! Я всегда испытывала трудности при решении задач с производными, и эта статья мне действительно помогла разобраться с этой темой. Автор подробно объяснил основные принципы производных и дал примеры задач, которые помогли мне лучше понять материал. Мне особенно понравился подход автора к решению задач. Он шаг за шагом разбирает каждое действие и даёт полезные советы, как найти производную функции. Кроме того, автор объяснил различные способы нахождения производной, что позволило мне выбрать наиболее удобный для меня метод. Теперь я чувствую себя увереннее при решении задач с производными. Статья помогла мне осознать, что производные математика — это не так уж и сложно, как мне всегда казалось. Я рекомендую эту статью всем, кто испытывает трудности с производными, и желает лучше разобраться в этой теме. Спасибо автору за отличную работу!