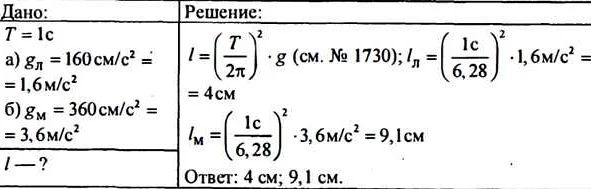
Найти длину математического маятника который за 20 с совершает 30 колебаний

На данной странице вы найдете информацию о том, как найти длину математического маятника, который совершает 30 колебаний за 20 секунд. Узнайте, как провести расчеты и применить соответствующую формулу для определения длины маятника.

Математический маятник — это система, состоящая из невесомой нити и точечной массы, которая может свободно колебаться под воздействием гравитационной силы. Он является одним из простейших примеров для изучения колебательных процессов в физике.

Длина математического маятника — один из его основных параметров, которая определяет период его колебаний. Период колебаний — это время, за которое маятник совершает одно полное колебание, то есть проходит от одной крайней точки до другой и обратно. Чтобы вычислить длину математического маятника, который совершает 30 колебаний за 20 секунд, нам необходимо знать период колебаний и количество колебаний.

Период колебаний математического маятника можно определить с помощью формулы:

T = 2π√(l/g)

где T — период колебаний, l — длина математического маятника, g — ускорение свободного падения (приближенное значение 9,8 м/с² на поверхности Земли). Таким образом, мы можем выразить длину маятника:

l = (T²*g)/(4π²)

Для нашего случая, где период колебаний T равен 20 секундам и количество колебаний равно 30, мы можем вычислить длину математического маятника по формуле:

l = (20²*9,8)/(4π²*30²)

После выполнения несложных математических вычислений, мы получим значение длины математического маятника. Таким образом, мы можем определить длину математического маятника, который совершает 30 колебаний за 20 секунд.

Математический маятник: как измерить длину за 30 колебаний

Для измерения длины математического маятника можно использовать метод, основанный на подсчете количества колебаний за определенный промежуток времени. В нашем случае, нам известно, что маятник совершает 30 колебаний за 20 секунд. Используя эту информацию, мы можем вычислить период колебаний маятника.

Период колебания математического маятника (T) можно вычислить по формуле:

T = t / n

где T — период колебания, t — время в секундах, за которое совершается n колебаний.

В нашем случае, у нас есть время — 20 секунд, и количество колебаний — 30. Подставляя эти значения в формулу, мы можем вычислить период колебания:

T = 20 секунд / 30 колебаний = 2/3 секунды

Теперь, зная период колебания маятника, мы можем вычислить его длину (L) по формуле:

L = g * T^2 / (4 * π^2)

где L — длина маятника, g — ускорение свободного падения (около 9,8 м/с^2), π — число пи (около 3,14).

Подставляя значения в формулу, получаем:

L = 9,8 м/с^2 * (2/3 секунды)^2 / (4 * 3,14^2) ≈ 0,39 метра

Таким образом, длина математического маятника, который совершает 30 колебаний за 20 секунд, составляет около 0,39 метра.

Видео по теме:

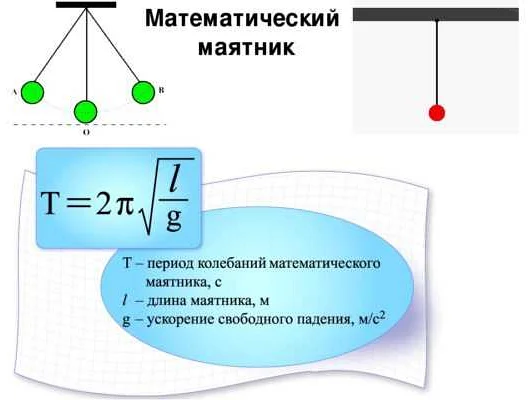
Определение математического маятника

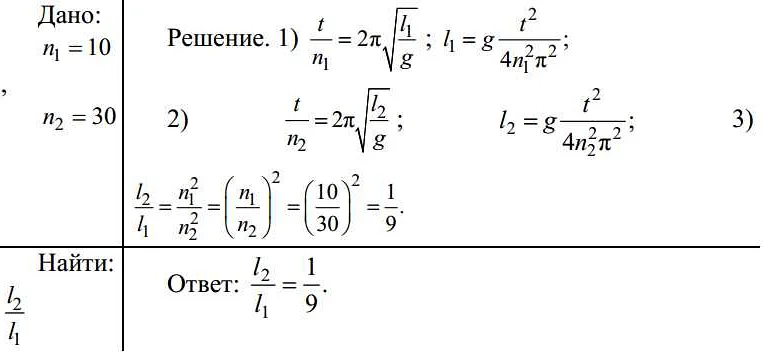
Движение математического маятника описывается законами механики и зависит от его длины, массы и амплитуды колебаний. Определение длины маятника является важным параметром, который влияет на его период и частоту колебаний.

Длина математического маятника измеряется от точки подвеса до центра масс. Изменение длины может привести к изменению периода колебаний маятника. Чем длиннее маятник, тем медленнее он будет колебаться, и наоборот.

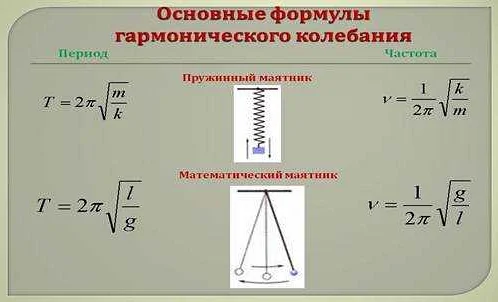
Для вычисления длины математического маятника, который совершает заданное количество колебаний за определенное время, требуется использовать формулу периода колебаний T = 2π√(L/g), где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

На основе заданного времени и количества колебаний можно вычислить период колебаний и, затем, подставить его в формулу для определения длины маятника. Таким образом, можно найти искомую длину математического маятника.

Формула периода колебаний

Для вычисления периода колебаний математического маятника, необходимо знать его длину. Формула, которая позволяет это сделать, имеет вид:

T = 2π√(L/g)

Где:

• T — период колебаний (время, за которое маятник совершает одно полное колебание);
• π — математическая константа, примерно равная 3.14159;
• L — длина математического маятника;
• g — ускорение свободного падения, примерно равное 9.8 м/с² на Земле.

Таким образом, для данного примера, где математический маятник совершает 30 колебаний за 20 секунд, мы можем использовать формулу для нахождения длины маятника:

T = 2π√(L/g)

Подставляя известные значения:

20 секунд = 30T

Таким образом, мы можем выразить длину маятника:

L = (T²g)/(π²)

Как сосчитать количество колебаний за 20 секунд

Для вычисления периода колебаний можно использовать формулу:

Формула	Значение
Период колебаний (T)	T = Время (t) / Количество колебаний (n)

В данном случае, нам известно время (20 секунд) и количество колебаний (30). Подставим эти значения в формулу:

Расчет	Значение
Период колебаний (T)	T = 20 секунд / 30 колебаний
	T ≈ 0.67 секунд

Теперь, когда у нас есть период колебаний (T), мы можем вычислить количество колебаний за 20 секунд, используя формулу:

Формула	Значение
Количество колебаний (n)	n = Время (t) / Период колебаний (T)

Подставим значения времени (20 секунд) и периода колебаний (0.67 секунд) в формулу:

Расчет	Значение
Количество колебаний (n)	n = 20 секунд / 0.67 секунд
	n ≈ 29.85

Таким образом, количество колебаний за 20 секунд составляет около 29.85. Округлив до целого числа, получим, что математический маятник совершает примерно 30 колебаний за 20 секунд.

Создание графика зависимости времени от количества колебаний

Для создания графика зависимости времени от количества колебаний необходимо выполнить следующие шаги:

1. Установить оси координат на графике, где ось абсцисс будет отображать количество колебаний, а ось ординат — время.
2. Выбрать подходящий масштаб для осей координат. Например, если количество колебаний составляет от 0 до 30, а время — от 0 до 20, то можно задать деления на осях координат каждые 5 единиц.
3. Построить точки на графике, соответствующие известным значениям времени и количеству колебаний. Например, если математический маятник совершает 30 колебаний за 20 секунд, то можно построить точку с координатами (30, 20).
4. Провести гладкую кривую через точки, чтобы визуально представить зависимость времени от количества колебаний. Для этого можно использовать метод интерполяции, например, полиномиальную интерполяцию.

В результате выполнения этих шагов на графике будет отображена зависимость времени от количества колебаний математического маятника.

Использование формулы для нахождения длины маятника

Для вычисления длины математического маятника, который совершает 30 колебаний за 20 секунд, мы можем использовать формулу периода колебаний маятника. Период колебаний (T) маятника определяется формулой:

T = 2π √ (l/g)

Где l — длина маятника, g — ускорение свободного падения.

Чтобы найти длину маятника (l), нам нужно переставить формулу и решить ее относительно l:

l = (T/2π)^2 * g

Для нашего случая, T = 20 секунд, g = 9.8 м/с^2 (ускорение свободного падения на Земле). Подставляя значения в формулу, получаем:

l = (20/2π)^2 * 9.8 ≈ 1.47 метра

Таким образом, длина математического маятника, который совершает 30 колебаний за 20 секунд, составляет около 1.47 метра.

Практическое применение измерений длины математического маятника

Одним из практических применений измерений длины математического маятника является определение гравитационного ускорения на заданной планете или в данной локации. Для этого необходимо измерить период колебаний маятника и длину подвеса. Используя формулу периода колебаний для математического маятника, можно вычислить гравитационное ускорение:

Период колебаний (T), секДлина подвеса (L), мГравитационное ускорение (g), м/с²

20

?

?

Для этого необходимо найти длину математического маятника, который совершает 30 колебаний за 20 секунд, используя формулу периода колебаний:

T = 2π√(L/g)

Где T — период колебаний, L — длина подвеса, g — гравитационное ускорение.

Исходя из данной формулы, можно выразить длину подвеса:

L = (T/2π)² * g

Подставляя известные значения в формулу, получаем:

L = (20/2π)² * g

Таким образом, измерение длины математического маятника позволяет нам определить гравитационное ускорение в данной локации. Эта информация может быть полезна в различных областях, таких как физика, геология, астрономия и инженерия. Например, в астрономии измерение гравитационного ускорения на других планетах помогает в изучении их поверхности и атмосферы.

Ошибки и погрешности при измерении

При проведении измерений всегда возникают ошибки и погрешности, которые могут влиять на точность результатов. Важно учитывать эти факторы при анализе и интерпретации полученных данных.

Ошибки могут быть вызваны различными причинами. Одной из основных является человеческий фактор – неправильная техника измерений, неточность при считывании данных и другие ошибки, допущенные оператором. Также возможны систематические ошибки, связанные с неисправностью или неточностью используемого оборудования.

Погрешности при измерении могут быть случайными или систематическими. Случайные погрешности обусловлены непредсказуемыми факторами, такими как колебания окружающей среды, дрожание рук оператора и другие внешние воздействия, которые могут приводить к непредсказуемым отклонениям результатов измерений. Систематические погрешности вызваны постоянными факторами, такими как неправильная калибровка приборов, неточность шкалы измерений и другие систематические ошибки.

Для уменьшения ошибок и погрешностей при измерении необходимо применять различные методы и техники. Важно правильно подготовиться к измерениям, провести несколько повторных измерений для получения среднего значения и учесть все возможные факторы, которые могут влиять на точность результатов.

Тип ошибкиОписание

Человеческий фактор	Ошибки, допущенные оператором при проведении измерений, такие как неточность при считывании данных или неправильная техника измерений.
Систематические ошибки	Ошибки, вызванные неисправностью или неточностью используемого оборудования, неправильной калибровкой приборов или другими постоянными факторами.
Случайные погрешности	Погрешности, обусловленные непредсказуемыми факторами, такими как колебания окружающей среды или дрожание рук оператора.
Систематические погрешности	Погрешности, вызванные постоянными факторами, такими как неправильная калибровка приборов или неточность шкалы измерений.

Вопрос-ответ:

Как вычислить длину математического маятника?

Длину математического маятника можно вычислить с помощью формулы: L = g * T^2 / (4 * π^2), где L — длина маятника, g — ускорение свободного падения (около 9,8 м/с^2 на Земле), T — период колебаний маятника (время, за которое маятник совершает одно полное колебание).

Какой период колебаний у математического маятника?

Период колебаний математического маятника можно вычислить с помощью формулы: T = 2 * π * sqrt(L / g), где T — период колебаний маятника, L — длина маятника, g — ускорение свободного падения (около 9,8 м/с^2 на Земле).

Как вычислить длину математического маятника, если известен его период колебаний?

Длину математического маятника можно вычислить с помощью формулы: L = g * T^2 / (4 * π^2), где L — длина маятника, g — ускорение свободного падения (около 9,8 м/с^2 на Земле), T — период колебаний маятника (время, за которое маятник совершает одно полное колебание).

Какую формулу использовать для вычисления длины математического маятника?

Формула для вычисления длины математического маятника: L = g * T^2 / (4 * π^2), где L — длина маятника, g — ускорение свободного падения (около 9,8 м/с^2 на Земле), T — период колебаний маятника (время, за которое маятник совершает одно полное колебание).

Как определить длину математического маятника, который совершает определенное количество колебаний за определенное время?

Для определения длины математического маятника, который совершает определенное количество колебаний за определенное время, необходимо воспользоваться формулой: L = g * (T / N)^2 / (4 * π^2), где L — длина маятника, g — ускорение свободного падения (около 9,8 м/с^2 на Земле), T — время, за которое маятник совершает N колебаний, N — количество колебаний.