Математические модели сигналов: что это такое и как они работают

Математическая модель сигналов — это формальное описание принципов, закономерностей и свойств, которые характеризуют любое явление передачи информации в виде электрических, световых, звуковых и других сигналов. В статье вы узнаете, что такое математическая модель сигналов и как ее можно использовать для предсказания и анализа различных явлений и процессов.

Современный мир насыщен информацией, и сигналы играют в нем огромную роль. Они используются во всех сферах жизни — в телекоммуникациях, медицинских приборах, радио и телевидении, производстве, науке и многих других областях.

Математическая модель сигналов — это способ представления сигналов в виде математических формул и уравнений. Эта модель позволяет анализировать и предсказывать поведение сигналов в условиях разных сред и взаимодействия с другими сигналами.

Моделирование сигналов играет ключевую роль во многих сферах, например, в проектировании и разработке устройств связи, контроля качества и диагностики оборудования, обработке изображений и звука. Также моделирование используется для изучения и оптимизации сигналов при передаче, уменьшении шума и других важных задачах.

Математическое моделирование сигналов помогает преодолеть сложности, связанные с техническими и физическими характеристиками сигналов, и получить более точные данные для принятия важных решений в различных сферах деятельности.

Математическая модель сигналов

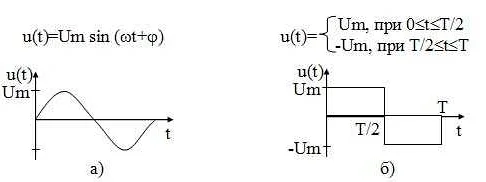
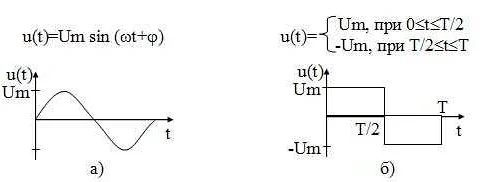
Сигнал – это любой процесс, который может быть замерен или воспроизведен. Например, звуковые волны, электрические сигналы, радиоволны и др. Сигналы используются в различных областях, таких как телекоммуникации, медицина, передача данных и другие.

Прежде чем можно будет проводить анализ или обработку сигнала, его необходимо представить в математической модели. Математическая модель – это упрощенное представление реального объекта или процесса в виде абстрактных математических соотношений и формул.

Для моделирования сигналов в математике используются функции, которые описывают изменение сигнала во времени. Наиболее распространенными функциями являются синусоидальные, косинусоидальные и экспоненциальные. С помощью этих функций можно описать различные характеристики сигнала, такие как амплитуда, частота, фаза и др.

Математическая модель сигнала позволяет проводить различные операции с сигналами, такие как фильтрация, преобразование и анализ. Например, сигнал может быть фильтрован, чтобы убрать шум или улучшить его качество. Сигналы также могут быть преобразованы в другие формы, чтобы изменить их свойства или упростить анализ. Например, с помощью преобразования Фурье можно раскрыть спектр сигнала.

Таким образом, математическая модель сигналов играет важную роль в практических приложениях, где необходимо анализировать и обрабатывать сигналы. Без математической модели сигнал был бы просто набором данных без возможности проводить анализ и использовать его в практических приложениях.

Видео по теме:

Что это такое?

Математическая модель сигналов — это математическое описание сигналов, которые мы измеряем и обрабатываем в нашей жизни. Сигнал может быть любым — звуком, светом, радиоволнами или другими электромагнитными волнами. Цель создания математической модели заключается в том, чтобы понять, как эти сигналы рождаются и распространяются, а также как их можно анализировать и обрабатывать.

Математическая модель сигналов может быть представлена в различных формах, таких как графические, аналитические или числовые. Она может быть линейной или нелинейной, дискретной или непрерывной. В зависимости от целей, которые мы преследуем, мы можем выбирать наиболее подходящую модель для конкретного сигнала.

Математическая модель сигналов является важным инструментом во многих областях науки и техники. Она используется для анализа и передачи звука, изображений, видео, радиоволн, синтеза и обработки музыки, распознавания голоса, а также в медицине, физике, химии, финансах и многих других областях.

Например, в медицине математическая модель сигналов используется для анализа электрокардиограммы (ЭКГ) и определения наличия сердечных заболеваний, регистрации мозговых потенциалов (ЭЭГ) и определения патологий в работе головного мозга. В финансовой сфере модель сигналов используется для прогнозирования изменений цен на рынке акций и определения оптимальных инвестиционных стратегий.

Как она работает?

Математическая модель сигналов представляет собой алгоритм, который принимает на вход различные сигналы и производит их анализ. Прежде чем начать работать с моделью, необходимо задать ее параметры, которые определяют основные характеристики сигналов.

После задания параметров модель начинает обрабатывать входящие сигналы. Она может проводить различные операции с ними, такие как фильтрация, преобразование, декомпозиция и другие. Затем модель производит анализ отфильтрованных сигналов и извлекает из них интересующую информацию.

Одним из примеров использования математической модели сигналов является анализ ЭКГ (электрокардиографической) записи. Модель принимает на вход сигнал, производит его фильтрацию от шума и других артефактов, а затем проводит расчеты, позволяющие определить состояние сердечной деятельности.

Математическая модель сигналов может использоваться в различных областях, таких как медицина, физика, инженерия и другие. Она позволяет производить высокоточный анализ сложных сигналов и извлекать из них полезную информацию, что делает ее незаменимым инструментом в современной науке и технологиях.

Вопрос-ответ:

Что такое математическая модель сигналов?

Математическая модель сигналов — это описание сигнала в форме математического уравнения, которое позволяет анализировать его свойства и использовать для различных целей, таких как обработка, передача, хранение и т.д.

Для чего нужна математическая модель сигналов?

Математическая модель сигналов нужна для анализа свойств и характеристик сигнала, для оптимизации процессов в обработке и передаче сигналов, для прогнозирования поведения сигнала в различных условиях, а также для разработки новых алгоритмов и методов обработки сигналов.

Какие сигналы могут быть описаны математической моделью?

Математическая модель может быть создана для любого типа сигнала, включая звуковые, видео-, радио-, электрические, оптические и другие сигналы. Но для каждого типа сигнала будут использоваться разные математические модели, соответствующие его особенностям.

Какие методы используются для создания математической модели сигнала?

Для создания математической модели сигнала могут использоваться такие методы, как метод наименьших квадратов, метод Фурье, метод Калмана, метод сигма-точек и другие методы. Выбор метода зависит от типа сигнала, его особенностей и целей использования модели.

Какие свойства сигнала могут быть анализированы с помощью математической модели?

С помощью математической модели сигнала можно анализировать такие его свойства, как амплитуда, частота, периодичность, фаза, спектральный состав, корреляционные свойства и др. Также с помощью математической модели можно определять наличие помех, искажений и других артефактов в сигнале.

Как математическая модель сигнала используется в обработке сигналов?

Математическая модель сигнала используется в обработке сигналов для фильтрации, усиления, декодирования, сжатия и других операций над сигналами. Например, можно использовать модель для удаления шумов и помех из сигнала или для улучшения качества воспроизведения сигнала.

Можно ли использовать математическую модель сигнала для прогнозирования поведения сигнала в будущем?

Да, с помощью математической модели сигнала можно проводить прогнозирование поведения сигнала в различных условиях, например, при изменении параметров окружающей среды или при изменении параметров оборудования в системе передачи. Однако, для этого требуется достаточно точная модель и точные данные о параметрах сигнала и среды передачи.

Для чего нужна математическая модель сигналов?

Математическая модель сигналов – это способ описания различных сигналов, чтобы можно было проанализировать их и использовать для решения различных задач. Такая модель представляет собой математическое выражение, которое описывает поведение сигнала в различных условиях.

Математическая модель сигналов нужна в первую очередь для анализа и прогнозирования поведения сигналов при различных воздействиях. Такая модель может использоваться в различных областях науки и техники, например, в электронике, телекоммуникациях, медицине и других областях.

Основная задача математической модели сигналов – это описание свойств сигнала и построение оптимальных алгоритмов его обработки. На основе такой модели можно рассчитывать общие характеристики сигнала, такие как частота, амплитуда и длительность, а также понимать, как различные параметры воздействуют на его поведение.

Таким образом, математическая модель сигналов играет важную роль в научных и инженерных исследованиях, а также в практических приложениях. Она позволяет точно описать поведение сигнала и создать на его основе эффективные решения для решения различных задач.

Какие виды сигналов моделируются?

В математических моделях сигналов моделируются различные виды сигналов, такие как:

• Аналоговые сигналы — это сигналы, которые изменяются во времени плавно и непрерывно. Примерами аналоговых сигналов могут служить сигналы синусоидальной формы, гармонические колебания в электрических цепях и акустические волны.
• Цифровые сигналы — это сигналы, которые принимают дискретные значения на определенных интервалах времени. Они используются в цифровой обработке сигналов и передаче информации по цифровым каналам связи. Примерами цифровых сигналов могут служить двоичные данные, цифровая музыка и видео.
• Периодические сигналы — это сигналы, которые повторяются через определенные промежутки времени. Примерами периодических сигналов могут служить синусоидальные колебания и электрические импульсы.
• Случайные сигналы — это сигналы, которые не могут быть описаны аналитически и содержат элементы случайности. Примерами случайных сигналов могут служить шумы, случайные блуждания и случайные события.

Знание и понимание различных типов сигналов позволяют создавать более точные математические модели, которые в свою очередь могут быть использованы в различных областях науки и технологии, таких как обработка сигналов, связь, медицина и наука о материалах.

Каковы применения моделирования сигналов в технике?

Моделирование сигналов находит широкое применение в различных областях техники, где необходимо анализировать, обрабатывать и передавать информацию через различные каналы связи.

Одним из наиболее распространенных применений моделирования сигналов является построение моделей телекоммуникационных систем. Такие системы используются для передачи голоса, данных, изображений и других типов информации. Моделирование сигналов позволяет определить и оценить такие параметры, как пропускная способность канала связи, скорость передачи данных и качество передаваемого сигнала.

Другой областью применения моделирования сигналов является создание систем управления и регулирования. Такие системы используются в широком спектре областей, включая автоматическое управление промышленным оборудованием, системы автопилотирования в авиации и навигации в морском транспорте. Моделирование сигналов позволяет проанализировать и определить оптимальные параметры системы управления и регулирования, такие как скорость реакции, точность и стабильность.

Также моделирование сигналов используется в проектировании электронных устройств и схем. Это может включать рисование схем, проведение аналитических расчетов и моделирование поведения электрических сигналов в различных условиях. Моделирование сигналов является необходимым инструментом для определения и устранения возможных проблем с сигналами до изготовления устройства.

В целом, моделирование сигналов играет ключевую роль в различных областях техники, позволяя определить и оценить параметры системы, проанализировать и устранить возможные проблемы и повысить ее качество и эффективность.

Как происходит обработка сигналов в цифровом виде на основе математической модели?

Обработка сигналов в цифровом виде осуществляется на основе математической модели, которая позволяет описать поведение сигнала во времени.

Эта модель может быть выражена в виде дискретных значений, численных последовательностей или матриц. Для обработки сигнала необходимо использовать специальные алгоритмы и методы, которые позволяют анализировать и изменять его свойства в соответствии с конкретными требованиями.

Одной из основных задач при обработке сигналов является фильтрация, которая позволяет убрать шум из сигнала и улучшить его качество. Для этого используются различные фильтры, такие как фильтры низких и высоких частот, полосо-задерживающие фильтры и др.

Также обработку сигналов в цифровом виде можно использовать для распознавания образов, сжатия данных, моделирования систем, анализа данных и многих других целей.

В целом, математическая модель сигналов является необходимой основой для обработки сигналов в цифровом виде. Она позволяет выполнять различные операции над сигналами с высокой степенью точности и эффективности, что делает ее одной из ключевых технологий в современной науке и технике.

Какие задачи можно решить, используя математическую модель сигналов?

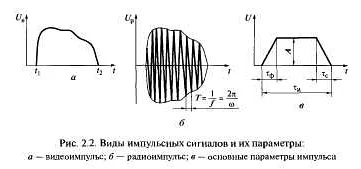
Математическая модель сигналов позволяет решать различные задачи, связанные с анализом и обработкой сигналов. Некоторые из них:

1. Анализ спектра сигналов: Математическая модель может помочь определить диапазон частот сигнала, который может быть использован для передачи информации. Это позволяет эффективнее использовать частотный ресурс и избежать помех от других источников.
2. Обнаружение и классификация сигналов: Математическая модель может использоваться для обнаружения наличия сигнала на фоне шума и его классификации. Это полезно, например, в радиолокации и в сигналах в медицинской диагностике.
3. Обработка и фильтрация сигналов: Математическая модель может использоваться для фильтрации сигналов, что помогает устранить шум и улучшить качество передачи информации. Один из методов фильтрации — применение цифровых фильтров, использующих математические алгоритмы для обработки сигнала.
4. Сжатие сигналов: Математическая модель может помочь сжимать сигналы, используя методы, такие как дискретное преобразование Фурье, вейвлет-преобразование и другие. Это позволяет передавать информацию более эффективно, что особенно важно в схемах передачи данных с ограниченной пропускной способностью.

Таким образом, математическая модель сигналов является мощным инструментом для анализа, обработки и передачи информации, и ее применение находит широкое применение во многих различных областях, начиная от телекоммуникаций и заканчивая медицинской диагностикой.

Какие инструменты используются для создания математической модели сигналов?

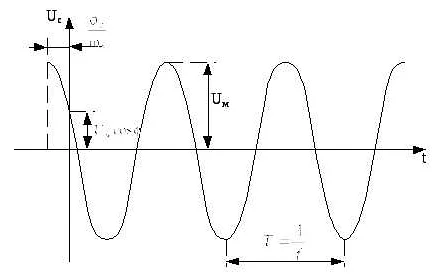
Для создания математической модели сигналов используются различные инструменты. Одним из основных инструментов является математическая статистика. В математической статистике используются методы анализа и оценки данных, а также методы построения статистических моделей.

Другим важным инструментом является теория вероятностей. Теория вероятностей позволяет определить вероятность того, что сигнал примет определенное значение в определенный момент времени. Это позволяет создавать математические модели, которые могут предсказывать поведение сигналов.

Еще одним инструментом является теория сигналов и систем. Теория сигналов и систем описывает, как сигналы могут быть представлены и преобразованы в другие формы. Она также описывает, как системы могут изменять и обрабатывать сигналы.

Также для создания математических моделей сигналов используются компьютерные программы. Компьютерные программы позволяют автоматически обрабатывать и анализировать большие объемы данных, что делает создание математических моделей более эффективным.

В целом, создание математической модели сигналов требует широкого спектра знаний и навыков. Важно выбрать подходящие инструменты для каждой конкретной задачи и уметь правильно их применять, чтобы создать точную и надежную математическую модель.

Можно ли применять математическую модель сигналов в медицине?

Математическая модель сигналов находит применение во многих областях, включая медицину. С помощью математических моделей можно анализировать и обрабатывать данные, получаемые с медицинского оборудования, такого как ЭКГ, ЭЭГ, МРТ и других.

Среди задач, решаемых с помощью математических моделей, выделяются такие, как:

• Анализ мозговых сигналов для диагностики психических расстройств
• Обработка сигналов ЭКГ для диагностики нарушений сердечной деятельности
• Анализ МРТ-изображений для выявления опухолей и других заболеваний

Одним из примеров применения математической модели в медицине является модель генерации ЭКГ, которая позволяет смоделировать электрическую активность сердца и получить возможные варианты кардиограммы. Это позволяет достичь более точной диагностики и разработки методов лечения.

Таким образом, математические модели сигналов являются важным инструментом для анализа и обработки медицинских данных, что позволяет улучшить диагностику и лечение различных заболеваний.

Какие будут новые направления развития моделирования сигналов в будущем?

В будущем моделирование сигналов будет все более улучшаться и точнее соответствовать реальным процессам. В настоящее время уже активно развиваются следующие направления:

• Моделирование ультразвуков. Развитие новых методов исследования ультразвука в медицине, науке и промышленности требует более точных и реалистичных моделей сигналов.
• Моделирование радиосигналов для исследования связи. В связи с развитием технологий беспроводной связи, моделирование радиосигналов станет еще важнее для создания надежных систем связи.
• Моделирование звуковых сигналов для виртуальной реальности. Создание более реалистичных звуковых эффектов в виртуальной реальности требует более точного моделирования звуковых сигналов.
• Моделирование голосовых сигналов для развития распознавания речи. Развитие систем распознавания речи требует более точного моделирования голосовых сигналов для обучения и тестирования алгоритмов.
• Моделирование изображений для компьютерного зрения. Решение задач компьютерного зрения требует точного моделирования изображений сигналов.

Таким образом, моделирование сигналов будет продолжать развиваться, становясь более точным и универсальным, что позволит создавать более сложные и качественные системы и устройства.