Кратное что это такое в математике

Кратное – это число, которое делится на другое число без остатка. Узнайте, как определить, является ли число кратным, и как использовать эту концепцию в математике.

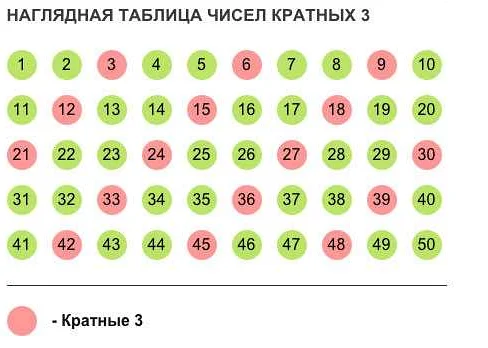
В математике понятие «кратное» играет важную роль при решении различных задач и задачек. Кратное числу называется число, которое делится на данное число без остатка. Например, числа 6, 12 и 18 являются кратными числа 3, потому что они делятся на 3 без остатка.

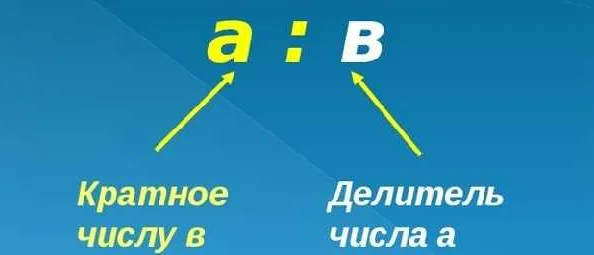
Определение кратности числа связано с делением. Если число а делится на число b без остатка, то оно называется кратным числу b. Математически это можно записать как а = b * с, где с — некоторое целое число. Например, число 15 является кратным числу 3, так как 15 = 3 * 5.

Определение кратного числа может быть полезным при решении задач на умножение и деление, поиск общего кратного двух чисел, а также при работе с дробями и пропорциями. Знание и понимание понятия кратности помогает упростить математические вычисления и сделать их более логичными и систематическими.

Важно отметить, что кратность числа не ограничивается только натуральными числами. Кратность может быть определена и для отрицательных чисел, десятичных дробей и дробей в общем виде. Главное условие — деление без остатка. Таким образом, понятие кратного числа является важным элементом в основах математики и находит применение во многих ее областях.

Определение кратного числа

Для определения кратного числа необходимо использовать деление с остатком. Если остаток равен нулю, то число является кратным. Например, число 15 является кратным числа 3, так как при делении 15 на 3 остаток равен нулю.

Чтобы определить кратность числа, можно использовать также таблицу умножения. Если число делится на другое число без остатка, то они находятся в одной строке или столбце таблицы умножения.

Кратное число можно также найти с помощью формулы. Пусть a — число, которое нужно проверить на кратность, а b — число, на которое проверяется кратность. Если остаток от деления a на b равен нулю, то a является кратным числом b.

Видео по теме:

Кратное числа: основные свойства

Основные свойства кратных чисел:

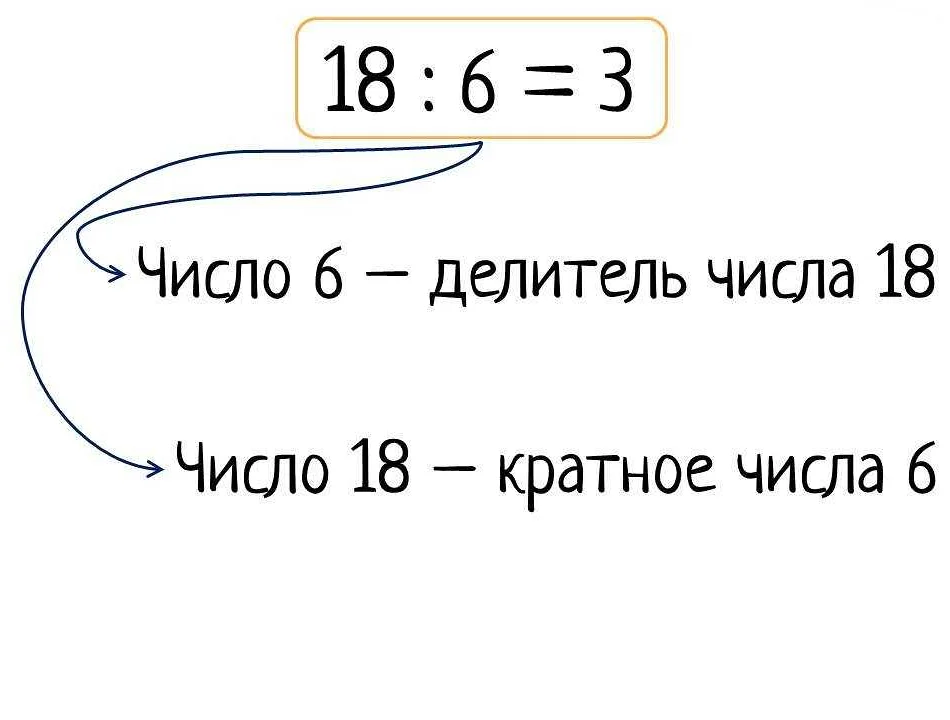
• Если число A кратно числу B, то число B также является делителем числа A.
• Если число A кратно числу B и число B кратно числу C, то число A также кратно числу C.
• Если число A кратно числу B, то сумма или разность чисел A и B также будет кратна числу B.
• Если число A кратно числу B и число B кратно числу C, то число A также кратно произведению чисел B и C.

Кратные числа имеют важное значение в алгебре и математическом анализе, так как они позволяют упростить множество вычислений и решений уравнений. Понимание основных свойств кратных чисел помогает в решении разнообразных математических задач и проблем.

Как определить, является ли число кратным

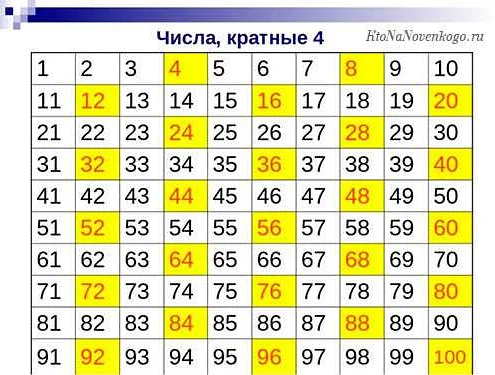
Чтобы определить, является ли число а кратным числу б, необходимо выполнить следующую проверку:

Если а делится на б без остатка, то число а является кратным числу б. Математически это можно записать как «а % б = 0», где символ «%» обозначает операцию взятия остатка от деления.

Например, число 10 является кратным числу 5, так как при делении 10 на 5 получается 0 в остатке: 10 % 5 = 0. А число 15 не является кратным числу 7, так как при делении 15 на 7 получается остаток: 15 % 7 = 1.

Используя данное правило, можно определить, является ли число кратным другому числу или нет.

Кратность числа и деление нацело

Деление нацело – это операция, при которой одно число делится на другое без остатка. Например, при делении числа 10 на 2, результатом будет число 5, так как 10 делится на 2 нацело.

Чтобы определить, является ли число кратным другому числу, необходимо проверить, делится ли оно нацело на это число. Если деление происходит без остатка, то число является кратным.

Например, число 15 является кратным числу 3, так как при делении 15 на 3 результатом будет число 5, которое не имеет дробной части.

Важно: Если число делится на другое число без остатка, то оно является кратным этому числу. Например, число 12 является кратным 1, 2, 3, 4, 6 и 12.

Кратное числа и остаток от деления

Остаток от деления — это число, которое остается после деления одного числа на другое.

Для определения кратности числа A числу B, необходимо проверить, равен ли остаток от деления числа A на число B нулю. Если остаток равен нулю, то число A является кратным числу B.

Например, число 12 кратно числу 6, так как при делении 12 на 6 остаток равен 0.

Остаток от деления может быть положительным или отрицательным числом, в зависимости от знаков делимого и делителя. Например, при делении -10 на 3, остаток будет равен -1.

Кратность числа может быть положительной или отрицательной. Например, число -24 является кратным числу 8, так как при делении -24 на 8 остаток равен 0.

Знание понятий кратного числа и остатка от деления помогает в решении задач по арифметике, алгебре и другим разделам математики.

Кратность и делители числа

Кратность числа может быть положительной или отрицательной. Положительная кратность означает, что число является делителем исходного числа, а отрицательная кратность — что число является делителем исходного числа, но с противоположным знаком.

Примеры кратных чисел:

• Число 6 является кратным числом 3, так как 3 можно разделить нацело на 6 без остатка.
• Число 12 также является кратным числом 3 и 6, так как 3 и 6 можно разделить нацело на 12 без остатка.
• Число 8 является кратным числом 2 и 4, так как 2 и 4 можно разделить нацело на 8 без остатка.

Кратность числа может быть полезна при решении различных задач в математике, физике и других науках. Она позволяет определить, какие числа являются делителями данного числа и использовать эту информацию для проведения различных операций и вычислений.

Кратное числа и делители: связь с простыми числами

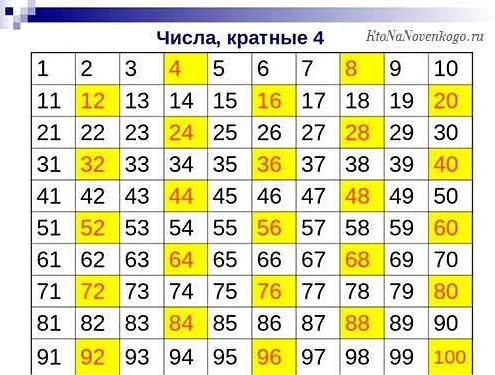
Делитель — это число, на которое делится другое число без остатка. Другими словами, если при делении одного числа на другое получается ноль в остатке, то второе число является делителем первого.

Кратные числа и делители тесно связаны между собой. Если число делится на другое число без остатка, то оно является кратным этого числа и делителем себя самого.

Простое число — это натуральное число, которое имеет только два делителя: 1 и само число. Простые числа также могут быть кратными и иметь делители, но они всегда имеют только два делителя.

Связь между кратными числами и простыми числами заключается в том, что если число является кратным простого числа, то оно также является кратным и всем его делителям. Например, число 10 является кратным простого числа 2, так как 10 делится на 2 без остатка. Оно также является кратным делителей простого числа 2: 1, 2, 5, 10.

Использование кратных чисел и делителей связано с различными областями математики, такими как арифметика, алгебра и теория чисел. Понимание этой связи позволяет решать различные задачи, связанные с делимостью чисел и их кратными.

Примеры кратных чисел и их применение в реальной жизни

1. Временные интервалы: Временные интервалы, такие как минуты, часы, дни, недели и годы, являются примерами кратных чисел. Например, 60 минут составляют один час, 24 часа составляют один день и 7 дней составляют одну неделю. Это позволяет нам измерять и организовывать время в повседневной жизни.
2. Деньги и валюта: Валюта также может быть измерена с использованием кратных чисел. Например, в США доллары разделены на центы, где 100 центов составляют один доллар. Это позволяет нам удобно работать с деньгами и проводить финансовые операции.
3. Музыкальные ноты: В музыке существуют кратные числа, которые определяют длительность нот. Например, целая нота равна 4 ударным, половина ноты равна 2 ударным, а четвертная нота равна 0.25 ударным. Это позволяет музыкантам играть и записывать музыку с определенным ритмом и темпом.
4. Транспорт и расписание: Кратные числа используются для составления расписания общественного транспорта, поездов и самолетов. Например, автобусы могут ходить каждые 15 минут, поезда могут отправляться каждый час, а самолеты могут прилетать каждые 30 минут. Это позволяет пассажирам планировать свои поездки и организовывать свое время с учетом кратных интервалов.

Это лишь некоторые примеры использования кратных чисел в реальной жизни. Они помогают нам измерять и организовывать различные аспекты нашего повседневного существования, обеспечивая удобство и порядок.

Вопрос-ответ:

Что такое кратное число в математике?

Кратным числом называется число, которое делится на другое число без остатка.

Как определить, является ли число кратным другому числу?

Для определения кратности числа нужно проверить, делится ли оно на другое число без остатка. Если деление происходит без остатка, то число является кратным.

Какие числа являются кратными 3?

Числа, которые делятся на 3 без остатка, являются кратными 3. Например, 3, 6, 9, 12 и так далее.

Являются ли отрицательные числа кратными?

Да, отрицательные числа также могут быть кратными. Например, -6, -9, -12 и так далее являются кратными числу 3.

Как определить, является ли число одновременно кратным двум разным числам?

Для определения кратности числа двум разным числам нужно проверить, делится ли оно и на первое число, и на второе число без остатка. Если деление происходит без остатка для обоих чисел, то число является кратным обоим.