Кто создал метод математической индукции

Метод математической индукции был создан математиком Блезом Паскалем в 17 веке. Он разработал этот метод для доказательства утверждений, основанных на принципе индукции, который ранее был сформулирован другими математиками. Метод математической индукции является одним из основных инструментов в математической логике и используется для доказательства широкого спектра утверждений и формулирования рекурсивных алгоритмов.

Метод математической индукции является одной из основных и наиболее мощных техник в математике. Этот метод позволяет доказывать утверждения для всех натуральных чисел, используя индуктивное рассуждение. Открытие этого метода является важной вехой в истории математики.

Впервые метод математической индукции был формализован и применен математиком Бернаром Болле, французским математиком XVIII века. Он использовал метод индукции для доказательства алгебраических утверждений, таких как формула для суммы арифметической прогрессии. В своих работах Бернар Болле описал и разработал все основные принципы метода математической индукции, которые используются и в настоящее время.

Однако, следует отметить, что идея индуктивного рассуждения была известна и использовалась ранее. В древних математических текстах можно найти примеры применения индукции. Например, древние математики использовали индукцию для доказательства утверждений о суммах квадратов натуральных чисел.

Таким образом, хотя Бернар Болле сформулировал и систематизировал метод математической индукции, он не является его первооткрывателем.

С течением времени метод математической индукции стал неотъемлемой частью математики и нашел широкое применение в различных областях, таких как алгебра, комбинаторика, теория чисел и дискретная математика. Многие известные математические теоремы и результаты были доказаны с использованием метода индукции.

Важным вкладом в развитие метода математической индукции является работа Георга Кантора, немецкого математика, основателя теории множеств. Он использовал метод индукции для доказательства основных свойств бесконечных множеств и разработал теорию трансфинитной индукции, которая позволяет проводить индуктивные рассуждения для бесконечных структур.

Таким образом, метод математической индукции является важным инструментом для математиков и играет ключевую роль в развитии и углублении научных знаний в области математики.

История появления метода математической индукции

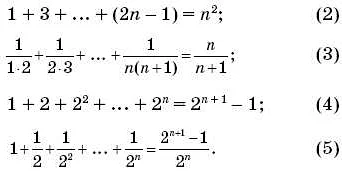
История развития метода математической индукции связана с работами многих ученых и математиков, включая Пьера Симона Лапласа, Карла Густава Якоби и многих других. Однако, основоположником этого метода считается Готфрид Вильгельм Лейбниц.

В своей работе «Математическая логика», опубликованной в 1684 году, Лейбниц впервые представил метод индукции, который он применил для доказательства ряда математических теорем. Лейбниц использовал метод индукции для доказательства утверждений о целых числах, рядов и бесконечно малых величинах.

С течением времени метод математической индукции стал все более распространенным и использовался во многих областях математики, включая алгебру, комбинаторику, теорию чисел и математическую логику. Этот метод стал неотъемлемой частью математического анализа и нашел применение в решении различных задач и доказательствах теорем.

Сегодня метод математической индукции является одним из основных инструментов в математике и используется в обучении, исследованиях и различных практических задачах.

Античность

Метод математической индукции, хотя и назван так, однако был известен еще в античных временах. Одним из первых античных математиков, которые использовали метод индукции, был греческий математик Евклид (около 300 г. до н.э.). В его работе «Начала» он применял метод индукции для доказательства различных свойств и теорем.

Однако, следует заметить, что сам термин «математическая индукция» был введен позже. Именно в 17 веке французский математик Блез Паскаль и итальянский математик Джузеппе Пеано дали определение и формализацию метода индукции, который мы сегодня используем.

Средние века

В период Средних веков математика развивалась в основном в монастырях, где монахи занимались исследованиями в различных областях науки. Однако, метод математической индукции не был изобретен в этот период.

Средневековые математики в основном использовали геометрические методы и алгебру, чтобы решать задачи. Они развивали теорию пропорций, работали с алгебраическими уравнениями и занимались геометрией.

Одним из важных математиков Средних веков был Фибоначчи, который ввел в Европе десятичную систему счисления и представил знаменитую последовательность чисел Фибоначчи.

Однако, метод математической индукции был разработан позже, в более поздние времена исследователями, такими как Пьер де Ферма и Блез Паскаль в XVII веке. Они использовали этот метод для доказательства их математических формул и теорем. С тех пор метод математической индукции стал широко используемым инструментом в математике и считается одним из основных методов доказательства.

Эра Просвещения

Эра Просвещения, также известная как Возрождение, была периодом интеллектуального и культурного развития, который произошел в Европе в XVII-XVIII веках. Она была отмечена ростом интереса к наукам, философии, искусству и образованию.

Во время Эпохи Просвещения, новые идеи и концепции о свободе, правах человека и рациональном мышлении начали распространяться по всей Европе. Философы и ученые стали активно исследовать и описывать мир с использованием рациональных методов и научных принципов.

Важным аспектом Эры Просвещения было установление нового подхода к математике и логике. Великие математики и ученые, такие как Рене Декарт, Блез Паскаль, Леонард Эйлер и Иоганн Бернулли, внесли значительный вклад в развитие математической индукции, метода, который играет важную роль в современной математике.

Метод математической индукции, изобретенный во время Эры Просвещения, стал мощным инструментом для доказательства утверждений и формализации математической логики. Он позволяет строить доказательства для бесконечных множеств утверждений, основываясь на их связи с предыдущими утверждениями.

Эра Просвещения оказала огромное влияние на развитие науки и образования в мире. Ее идеи и принципы продолжают оставаться актуальными и важными до сегодняшнего дня, и метод математической индукции является одним из ярких проявлений этой эры.

Исторические споры и открытия

Одним из первых, кто применил метод математической индукции, был французский математик Блез Паскаль. В своей работе «Трактат о треугольнике Аритметике» он использовал этот метод для доказательства утверждений, связанных с числовыми рядами.

Однако признание метода математической индукции как фундаментального инструмента математики пришло позже, благодаря работам других выдающихся математиков.

Одним из таких математиков был немецкий математик Карл Гаусс. В своей работе «Доказательство делимости числа на все его меньшие делители» Гаусс применил метод математической индукции для доказательства утверждений о делимости чисел.

Другим важным вкладом в развитие метода математической индукции была работа немецкого математика Карла Вайерштрасса. В своих трудах он уточнил и формализовал этот метод, установив четкие правила его применения и доказательства.

Таким образом, история метода математической индукции связана с именами выдающихся математиков, которые внесли свой вклад в его развитие и признание. Вопрос о том, кто именно изобрел метод математической индукции, до сих пор остается предметом споров и дискуссий.

Важные вклады известных математиков

Блез Паскаль (1623-1662)

Блез Паскаль был французским математиком и философом, который сделал важные открытия в области комбинаторики и теории вероятностей. Он впервые сформулировал метод математической индукции и использовал его в своей работе «Трактат о треугольнике Аритметики».

Готфрид Вильгельм Лейбниц (1646-1716)

Готфрид Вильгельм Лейбниц был немецким ученым, математиком и философом. Он разработал идеи бесконечной последовательности и ввел понятие рекурсии, что существенно способствовало развитию метода математической индукции.

Карл Фридрих Гаусс (1777-1855)

Карл Фридрих Гаусс был немецким математиком и физиком, который сделал важный вклад в различные области математики. Он использовал метод математической индукции в своей работе по теории чисел и доказал несколько важных теорем.

Давид Хильберт (1862-1943)

Давид Хильберт был немецким математиком, который сформулировал список 23 нерешенных проблем в математике. Он использовал метод индукции для доказательства многих теорем из различных областей математики и сделал значительный вклад в развитие этого метода.

Эти математики и многие другие сделали важные вклады в развитие метода математической индукции, что позволило решить множество математических задач и развить новые области математики.

Применение метода в современной науке

Одной из областей, где метод математической индукции находит применение, является теория графов. В этой области метод используется для доказательства теорем о свойствах графов, например, о том, что любой связный граф содержит остовное дерево.

Метод также активно применяется в дискретной математике, в теории чисел и в комбинаторике. Он позволяет доказывать различные утверждения о целых числах, комбинаторных структурах и многих других объектах.

Более того, метод индукции нашел свое применение в программировании и алгоритмике. В программировании индуктивные алгоритмы используются для решения задач, где требуется построить рекурсивные структуры данных или рекурсивно обрабатывать данные.

Таким образом, метод математической индукции остается одним из фундаментальных инструментов современной науки. Его применение распространено в различных областях и позволяет решать сложные задачи, основанные на рекуррентных свойствах объектов.

Видео по теме:

Вопрос-ответ:

Кто изобрел метод математической индукции?

Метод математической индукции был изобретен математиком Блезом Паскалем в 17 веке.

Как работает метод математической индукции?

Метод математической индукции заключается в доказательстве утверждений для всех натуральных чисел. Сначала доказывается базовое утверждение для первого числа (например, для n=1). Затем предполагается, что утверждение верно для некоторого числа n=k и доказывается, что оно верно для n=k+1. Таким образом, используя индукцию, утверждение можно доказать для всех натуральных чисел.

Каковы важные вклады метода математической индукции?

Метод математической индукции имеет огромное значение в математике и других науках. Он позволяет доказывать утверждения для бесконечного числа значений и обеспечивает строгое математическое обоснование. Метод индукции широко применяется в различных областях, включая дискретную математику, теорию чисел, комбинаторику и математическую логику.

Какой вклад внес Блез Паскаль в развитие метода математической индукции?

Блез Паскаль внес значительный вклад в развитие метода математической индукции, представив его в систематической форме. Он разработал общие правила и методы доказательства, которые позволили применять индукцию в широком спектре математических задач. Благодаря его работе, метод индукции стал одним из основных инструментов математического исследования.

Какие еще методы доказательства существуют помимо математической индукции?

Помимо метода математической индукции, существуют и другие методы доказательства, такие как доказательство от противного, доказательство с помощью контрапозиции, доказательство методом отделения случаев и др. Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной задачи и условий.

Какой ученый изобрел метод математической индукции?

Метод математической индукции был разработан итальянским математиком Франческо Маурицио Моргиа в 16 веке.

Ключевые понятия метода математической индукции

Базовый шаг — это первый шаг в методе математической индукции. Он заключается в доказательстве истинности утверждения для начального значения переменной. Обычно это значение равно 1 или 0, в зависимости от конкретной задачи.

Шаг индукции — это второй шаг в методе математической индукции. Он заключается в доказательстве, что если утверждение истинно для некоторого значения переменной, то оно также будет истинно для следующего значения переменной. Это доказывается с помощью предположения индукции и аксиомы математической индукции.

Предположение индукции — это предположение о том, что утверждение истинно для некоторого значения переменной.

Аксиома математической индукции — это утверждение, которое гарантирует истинность утверждения для всех натуральных чисел, начиная с базового значения переменной. Аксиома математической индукции формулируется следующим образом: если утверждение истинно для некоторого значения переменной, то оно также будет истинно для следующего значения переменной.

Используя базовый шаг и шаг индукции, можно доказать истинность утверждения для всех натуральных чисел путем последовательного применения шага индукции.

Разновидности и модификации метода математической индукции

Одной из разновидностей метода математической индукции является сильная индукция. В этом случае, вместо предположения, что утверждение верно для некоторого числа k, мы предполагаем, что оно верно для всех чисел, меньших k. Затем, используя это предположение, мы доказываем, что утверждение верно и для числа k. Такой подход позволяет решать задачи, которые не могут быть решены обычной индукцией.

Ещё одной модификацией метода математической индукции является принцип минимального контрпримера. Суть этого метода заключается в том, что мы предполагаем, что утверждение неверно для некоторого числа n, а затем находим наименьшее такое число. Затем мы доказываем, что утверждение все-таки верно для этого числа, что приводит к противоречию. Этот метод позволяет доказывать отрицание утверждения и может быть полезен, когда прямое применение обычной индукции затруднено.

Кроме того, в математике существуют и другие модификации метода математической индукции, которые применяются в различных областях. Например, индукция может быть использована для доказательства утверждений о последовательностях, множествах, или для доказательства математических формул. Каждая из этих модификаций имеет свои особенности и применяется в зависимости от конкретной задачи.

Таким образом, разновидности и модификации метода математической индукции расширяют его применимость и позволяют доказывать более сложные утверждения. Они играют важную роль в различных областях математики и помогают математикам решать разнообразные задачи.