Что такое математическая модель и математическое моделирование

Математическая модель — это абстрактное представление реального явления или процесса с помощью математических символов и выражений. Математическое моделирование — это процесс создания и использования математических моделей для изучения, анализа и прогнозирования различных явлений и процессов. Узнайте больше о понятии математической модели и ее применении в различных областях на нашем сайте.

Математическая модель является одним из основных инструментов анализа и исследования сложных систем в различных областях науки и техники. Она представляет собой абстракцию реального объекта или процесса, которую можно описать с помощью математических формул и уравнений. Математические модели позволяют изучать и предсказывать различные аспекты системы, такие как ее поведение, эффективность, стабильность и т.д.

Основной целью математического моделирования является получение количественных и качественных оценок и прогнозов, которые могут быть использованы для принятия решений или планирования деятельности. Математическое моделирование позволяет анализировать сложные системы, которые не всегда могут быть изучены или изменены в реальных условиях. Оно также позволяет проводить эксперименты и тестирование гипотез в контролируемой и безопасной среде.

Математическое моделирование широко применяется во многих областях, таких как физика, химия, биология, экономика, социология и др. Оно помогает исследователям и ученым понять сложные взаимодействия и зависимости между различными переменными и факторами, а также предсказать результаты их взаимодействия.

В процессе математического моделирования используются различные методы и техники, включая аналитические и численные методы, статистический анализ, оптимизацию и т.д. Однако, создание математической модели является творческим процессом, требующим глубокого понимания исследуемой системы и умения выбрать наиболее подходящие математические концепции и методы для ее описания.

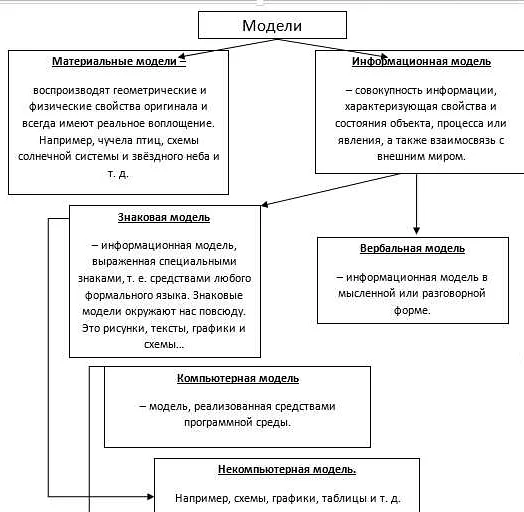
Что такое математическая модель?

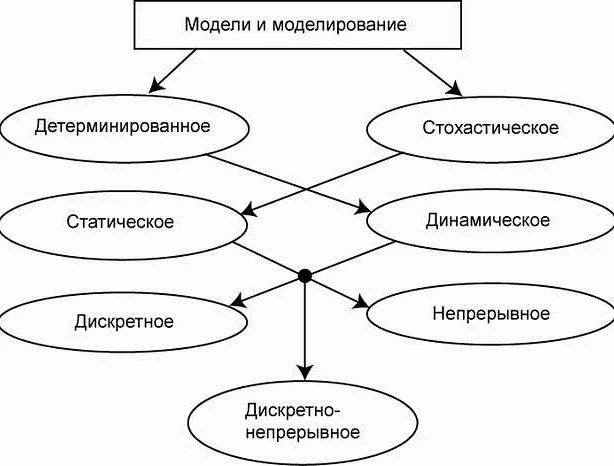
Математическая модель состоит из нескольких составляющих:

• Математических переменных: символы, которые представляют измеряемые величины или параметры модели.
• Промежуточных и зависимых переменных: переменные, которые выражаются через математические выражения и уравнения на основе математических переменных.
• Функций: математические выражения, которые описывают зависимость между переменными и характеризуют свойства модели.
• Уравнений: математические соотношения, которые связывают переменные и определяют свойства модели.

Математическая модель позволяет решать разнообразные задачи, такие как прогнозирование, оптимизация, симуляция и анализ. Она широко используется в различных областях науки, техники, экономики и других дисциплинах для исследования и понимания сложных систем и процессов.

Основные принципы математического моделирования

Для успешного математического моделирования существуют определенные принципы, которые позволяют создать адекватную и достоверную модель:

1. Упрощение и абстракция: Для создания модели необходимо выделить основные характеристики и свойства системы, игнорируя второстепенные детали. Упрощение позволяет сделать модель более понятной и управляемой.
2. Математическое описание: Модель должна быть представлена в виде математических уравнений или функций. Это позволяет проводить аналитический и численный анализ модели, а также решать уравнения для получения результатов.
3. Верификация и валидация: Проверка и подтверждение достоверности модели являются важными этапами. Верификация — это сравнение модели с реальными данными или другими подтвержденными моделями. Валидация — это проверка модели на соответствие поставленным целям и задачам.
4. Прогнозирование и экстраполяция: Модель должна быть способна предсказывать поведение системы в различных условиях и на разных временных шкалах. Это позволяет проводить эксперименты и изучать возможные сценарии развития системы.
5. Итерационный подход: Математическое моделирование — это итерационный процесс, который включает в себя последовательное уточнение и улучшение модели. При обнаружении ошибок или несоответствий модель может быть пересмотрена и доработана.
6. Интерпретация результатов: Полученные результаты модели должны быть интерпретированы и анализированы с учетом их значения и влияния на реальную систему. Это позволяет делать выводы и принимать решения на основе результатов моделирования.

Соблюдение этих принципов позволяет создать надежную, полезную и эффективную математическую модель, которая может быть использована для изучения и улучшения различных систем и явлений в науке, технике, экономике и других областях знания.

Зачем нужны математические модели?

Основная задача математических моделей — предсказать результаты реальных событий и экспериментов, а также изучать их свойства и особенности. Математические модели позволяют проводить различные численные исследования, эксперименты и симуляции, что значительно упрощает и ускоряет процесс изучения сложных систем и явлений.

Преимущества использования математических моделей включают:

• Предсказуемость и контролируемость: Математические модели позволяют предсказывать результаты исследований и экспериментов, что помогает планировать и контролировать процессы.
• Экономия времени и ресурсов: Математическое моделирование позволяет изучать системы и явления в виртуальной среде, что значительно сокращает расходы на реальные эксперименты и исследования.
• Упрощение сложных процессов: Математические модели позволяют упростить сложные явления и процессы, разбивая их на более простые компоненты и связи между ними.
• Новые открытия и инновации: Математическое моделирование может помочь обнаружить новые закономерности и взаимосвязи, которые не сразу видны при изучении реальных объектов и систем.

Таким образом, математические модели играют важную роль в науке, технике и многих других областях, помогая нам лучше понимать и управлять сложными системами и процессами.

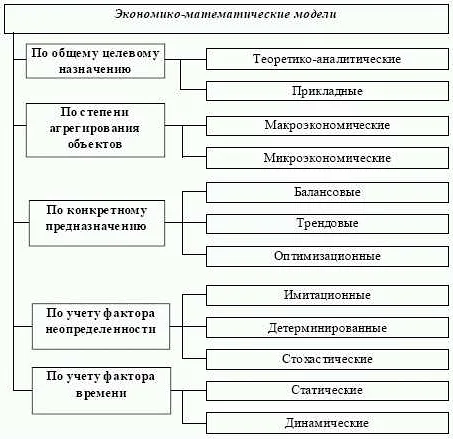
Примеры применения математических моделей

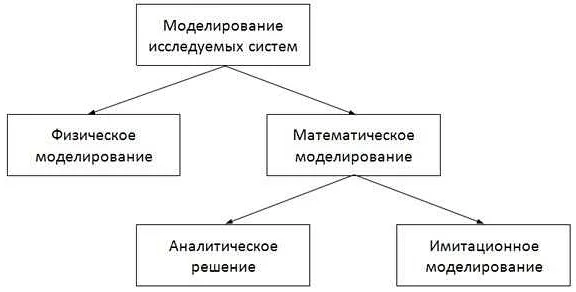
Математические модели широко применяются в различных областях науки, техники, экономики и других областях человеческой деятельности. Вот несколько примеров использования математических моделей:

Область примененияПример моделиЦель моделирования

Физика	Модель движения тела под действием силы тяжести	Предсказание траектории движения, вычисление времени падения
Экономика	Модель спроса и предложения на рынке	Определение равновесной цены и количества товара
Биология	Модель популяционной динамики	Изучение изменений численности популяции во времени
Транспорт	Модель трафика на дороге	Прогнозирование времени в пути, оптимизация дорожной инфраструктуры
Медицина	Модель распространения инфекции	Анализ эффективности превентивных мер и прогнозирование развития эпидемии

Эти примеры демонстрируют, что математическое моделирование является мощным инструментом для анализа и прогнозирования различных явлений и процессов. Оно позволяет упростить сложные реальные системы, выявить основные закономерности и принять обоснованные решения на основе полученных результатов.

Математическое моделирование в научных исследованиях

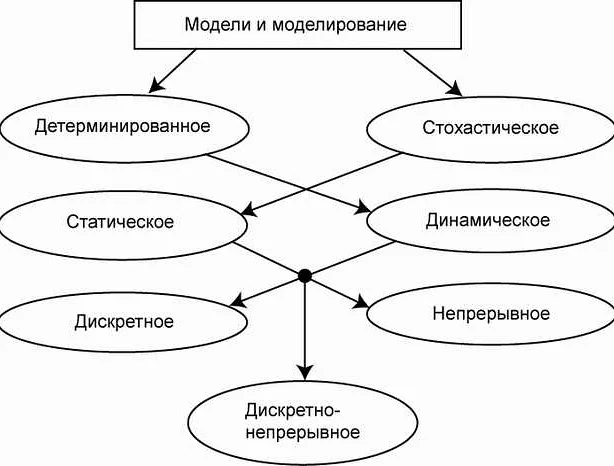
Математическая модель представляет собой формальное описание системы с помощью математических уравнений и отношений. Она описывает основные характеристики системы и ее взаимодействие с окружающей средой. Математические модели могут быть различными: дискретными или непрерывными, линейными или нелинейными, статическими или динамическими.

Математическое моделирование позволяет ученым проводить эксперименты с системой в виртуальной среде, что облегчает и ускоряет исследовательский процесс. Они могут изменять параметры модели, наблюдать изменение ее поведения и проверять различные гипотезы. Таким образом, математическое моделирование позволяет получить новые знания о системе, которые могут быть использованы для принятия решений и оптимизации ее работы.

Применение математического моделирования в научных исследованиях позволяет ученым решать сложные задачи, которые не могут быть решены с помощью аналитических методов или экспериментальных данных. Оно позволяет предсказывать поведение системы в различных условиях, а также исследовать ее чувствительность к изменениям параметров. Математические модели могут быть использованы для изучения физических процессов, биологических систем, экономических явлений, социальных взаимодействий и многих других областей.

Однако следует отметить, что математическое моделирование имеет свои ограничения и предположения, которые могут влиять на точность результатов. Поэтому важно проводить проверку моделей на экспериментальных данных и учитывать их ограничения при интерпретации результатов.

Вывод: Математическое моделирование является мощным инструментом в научных исследованиях, позволяющим ученым изучать и предсказывать поведение сложных систем. Оно позволяет проводить виртуальные эксперименты, исследовать различные условия и оптимизировать работу системы. Однако необходимо учитывать ограничения моделей и проверять их на экспериментальных данных для достоверных результатов и выводов.

Математическое моделирование в технике и инженерии

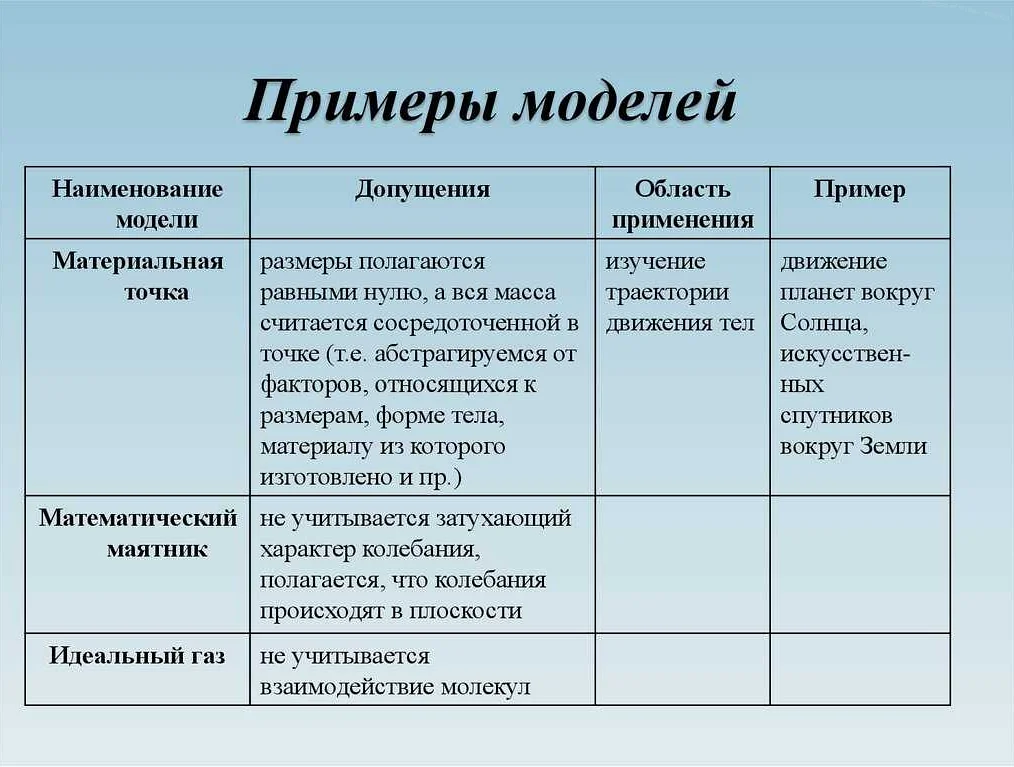
Математическое моделирование широко применяется в различных областях техники и инженерии, таких как авиационная и космическая промышленность, электроника, машиностроение, энергетика и другие. Оно позволяет инженерам и специалистам разрабатывать и улучшать продукты и системы, анализировать и прогнозировать их работу, оптимизировать параметры и ресурсы.

Математическое моделирование включает в себя такие этапы, как формулирование проблемы, выбор и определение математической модели, решение уравнений и анализ результатов. В процессе моделирования используются различные методы и алгоритмы, такие как дифференциальные уравнения, статистические методы, оптимизация и т. д.

Одной из основных задач математического моделирования в технике и инженерии является оптимизация систем. С помощью моделирования можно исследовать различные варианты решений, определить оптимальные параметры и условия работы системы, а также предсказать ее поведение в различных ситуациях.

Важным аспектом математического моделирования в технике и инженерии является проверка и верификация моделей. Это позволяет убедиться в достоверности и точности модели и ее соответствии реальным данным и явлениям. Также проводится валидация модели, чтобы убедиться, что она действительно описывает и предсказывает поведение системы.

Математическое моделирование является неотъемлемой частью технического и инженерного анализа, проектирования и оптимизации систем. Оно позволяет сократить время и затраты на создание и испытание реальных прототипов, а также предоставляет возможность исследовать системы в различных условиях и сценариях.

Основные понятия математического моделирования

Основные понятия математического моделирования включают:

Объект моделирования	– это реальная система или явление, которые подлежат изучению и описанию в виде математической модели. Объект моделирования может быть физическим объектом (например, автомобиль), биологическим процессом (например, рост популяции) или социальной системой (например, экономика).
Математическая модель	– это абстрактное представление объекта моделирования с использованием математических понятий и формул. Математическая модель может быть представлена в виде уравнений, систем уравнений, графов или других математических структур.
Переменные	– это величины, которые описывают характеристики объекта моделирования. Математические переменные могут быть непрерывными (например, время) или дискретными (например, количество).
Параметры	– это величины, которые задаются внешними условиями и не меняются в процессе моделирования. Параметры могут быть постоянными (например, гравитационная постоянная) или изменяющимися (например, температура).
Уравнения модели	– это математические соотношения, которые описывают зависимости между переменными и параметрами в математической модели. Уравнения модели могут быть линейными или нелинейными, аналитическими или численными.
Задача моделирования	– это постановка и решение задачи на основе математической модели. Задача моделирования может быть направлена на прогнозирование, оптимизацию, анализ или управление реальными системами или явлениями.

Математическое моделирование является мощным инструментом для исследования и понимания сложных систем и процессов в различных областях науки, техники и экономики. Оно позволяет проводить эксперименты в виртуальной реальности, анализировать различные сценарии и прогнозировать поведение системы в различных условиях.

Вопрос-ответ:

Зачем нужна математическая модель?

Математическая модель используется для описания и изучения реальных явлений и процессов. Она позволяет упростить сложную систему, выделить главные факторы и взаимосвязи между ними, а также предсказывать поведение системы в различных условиях.

Какие основные принципы лежат в основе математического моделирования?

Основные принципы математического моделирования включают выбор модельной системы, определение переменных и параметров модели, построение уравнений, учет условий и граничных условий, а также верификацию и валидацию модели.

Какие проблемы могут возникнуть при построении математической модели?

При построении математической модели могут возникнуть такие проблемы, как неоднозначность определения переменных и параметров, сложность построения уравнений, неучет влияния случайных факторов, недостаточная точность данных для верификации и валидации модели.

Какую роль играют математические модели в научных исследованиях?

Математические модели играют важную роль в научных исследованиях. Они позволяют проверить гипотезы, предсказать результаты экспериментов, исследовать системы, для которых экспериментальные данные трудно или невозможно получить, а также оптимизировать процессы и принимать обоснованные решения.

Какие методы можно использовать для решения математических моделей?

Для решения математических моделей можно использовать различные методы, включая аналитические методы (поиск аналитического решения в явном виде), численные методы (решение уравнений и систем уравнений с помощью численных методов), аппроксимационные методы (приближенное представление решения) и др.

Видео по теме: