На рисунке изображен математический маятник в какой точке кинетическая энергия маятника максимальна

Узнайте, в какой точке кинетическая энергия математического маятника достигает максимума. Подробное объяснение и иллюстрация.

Математический маятник является одной из самых известных моделей в физике, которая используется для изучения колебаний. Он представляет собой маятник, подвешенный на нерастяжимой нити и движущийся в плоскости. Важной характеристикой маятника является его кинетическая энергия, которая определяет его движение и зависит от его положения.

Кинетическая энергия маятника определяется формулой K = (1/2) * m * v^2, где K — кинетическая энергия, m — масса маятника, v — его скорость. Очевидно, что чем больше скорость маятника, тем больше его кинетическая энергия.

Однако, скорость маятника зависит от его положения. Скорость маятника достигает максимального значения в его нижней точке, когда его потенциальная энергия минимальна. В этой точке маятник имеет наибольшую скорость и, соответственно, наибольшую кинетическую энергию.

Таким образом, кинетическая энергия математического маятника максимальна в его нижней точке.

Математический маятник: точка максимальной кинетической энергии

Математический маятник представляет собой механическую систему, состоящую из точечной массы, закрепленной на невесомой нерастяжимой нити, и движущейся по дуге окружности. В такой системе на маятник действуют силы тяжести и натяжения нити.

Кинетическая энергия математического маятника определяется как энергия его движения и зависит от его скорости. Максимальная кинетическая энергия достигается в тот момент, когда маятник находится в наиболее удаленной точке от положения равновесия, т.е. в точке кульминации.

Для определения точки максимальной кинетической энергии математического маятника можно использовать закон сохранения механической энергии. Согласно этому закону, сумма потенциальной и кинетической энергии остается постоянной на всем пути движения маятника.

Наибольшая потенциальная энергия достигается в точке кульминации, так как наибольшая высота над уровнем положения равновесия соответствует наибольшей потенциальной энергии. Следовательно, в этой точке кинетическая энергия математического маятника будет максимальной.

Таким образом, точка максимальной кинетической энергии математического маятника совпадает с его точкой кульминации, где маятник находится на наибольшей высоте. В этой точке кинетическая энергия достигает своего максимального значения, а потенциальная энергия минимального.

ПараметрЗначение

Масса маятника	m
Длина нити	L
Угол отклонения от вертикали	θ
Скорость маятника	v
Кинетическая энергия	K = (1/2)mv^2
Потенциальная энергия	U = mgL(1 — cosθ)

Таким образом, для определения точки максимальной кинетической энергии математического маятника необходимо знать его массу, длину нити, а также угол отклонения от вертикали. При правильном использовании формул и учете всех параметров можно определить максимальное значение кинетической энергии и понять, в какой точке оно достигается.

Определение и принцип действия

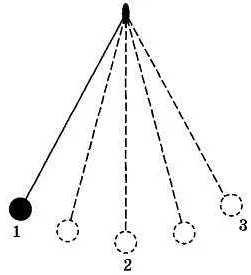
Принцип действия математического маятника основывается на законах сохранения энергии и механического движения. Когда маятник отклоняется от положения равновесия и отпускается, начинается его колебательное движение.

В процессе колебаний маятника его потенциальная энергия, связанная с высотой подвеса, переходит в кинетическую энергию и обратно. Верхняя точка траектории движения маятника является точкой максимальной потенциальной энергии и минимальной кинетической энергии, а нижняя точка — точкой максимальной кинетической энергии и минимальной потенциальной энергии.

Таким образом, кинетическая энергия математического маятника будет максимальной в нижней точке его траектории, когда его скорость будет наибольшей, а потенциальная энергия будет минимальной.

Влияние массы маятника на кинетическую энергию

Математический маятник представляет собой систему, состоящую из точечной массы, подвешенной на невесомой нити, которая прикреплена к точке подвеса. Кинетическая энергия маятника определяется его массой и скоростью.

Влияние массы маятника на кинетическую энергию можно объяснить следующим образом. С увеличением массы маятника, его инерция также увеличивается. Это означает, что для изменения скорости маятника требуется большее количество энергии. Таким образом, при увеличении массы маятника, его кинетическая энергия также увеличивается.

Это можно проиллюстрировать с помощью таблицы, в которой представлены значения кинетической энергии для разных масс маятника:

Масса маятника (кг)Кинетическая энергия (Дж)

0.5	0.25
1	0.5
1.5	0.75
2	1

Из таблицы видно, что с увеличением массы маятника, его кинетическая энергия увеличивается пропорционально.

Таким образом, можно сделать вывод, что масса маятника оказывает прямое влияние на его кинетическую энергию. Чем больше масса маятника, тем больше его кинетическая энергия при одинаковой скорости. Это является важным фактором при анализе движения математического маятника и его энергетических характеристик.

Связь длины подвеса и кинетической энергии

Кинетическая энергия математического маятника зависит от его скорости и массы. Когда маятник находится в точке максимального отклонения, его скорость равна нулю, а следовательно, и кинетическая энергия также равна нулю. По мере движения маятника вниз, его скорость возрастает, и кинетическая энергия увеличивается.

Однако, при изменении длины подвеса, период колебаний маятника также меняется. Чем длиннее подвес, тем медленнее маятник будет совершать колебания. Следовательно, кинетическая энергия маятника будет достигать своего максимума в точке, где его скорость максимальна. В этой точке кинетическая энергия будет наибольшей.

Таким образом, существует прямая связь между длиной подвеса математического маятника и его кинетической энергией. Чем длиннее подвес, тем выше максимальное значение кинетической энергии достигается маятником.

Зависимость кинетической энергии от начального угла отклонения

Кинетическая энергия математического маятника находится в непосредственной зависимости от его начального угла отклонения. Чем больше этот угол, тем больше кинетическая энергия системы.

Начальный угол отклонения определяет положение маятника относительно равновесия. При малых углах отклонения кинетическая энергия практически не отличается от потенциальной энергии, а при больших углах она достигает максимального значения.

Это связано с тем, что при большем угле отклонения маятник обладает большей скоростью, что приводит к увеличению его кинетической энергии. В то же время, потенциальная энергия в этом случае уменьшается.

Таким образом, для определения максимальной кинетической энергии математического маятника необходимо отклонить его наибольшим углом от равновесия.

Влияние сопротивления среды на кинетическую энергию

Сопротивление среды может значительно влиять на кинетическую энергию математического маятника. Кинетическая энергия определяется как энергия движения тела и зависит от его массы и скорости.

В отсутствие сопротивления среды, кинетическая энергия математического маятника будет максимальной в точке его максимального отклонения от положения равновесия. В этой точке маятник имеет максимальную скорость, что приводит к увеличению его кинетической энергии.

Однако при наличии сопротивления среды, энергия будет постепенно теряться за счет силы трения, действующей на маятник. Это приводит к замедлению его движения и, следовательно, к уменьшению кинетической энергии.

Таким образом, влияние сопротивления среды на кинетическую энергию математического маятника заключается в том, что оно приводит к ее уменьшению. Чем больше сопротивление среды, тем быстрее маятник замедляется и тем меньше его кинетическая энергия в любой точке его движения.

Важно отметить, что влияние сопротивления среды на кинетическую энергию может быть незначительным для математического маятника с малым коэффициентом трения. В таком случае, кинетическая энергия маятника будет близка к максимальной в точке его максимального отклонения.

Итак, сопротивление среды влияет на кинетическую энергию математического маятника, уменьшая ее по мере замедления его движения.

Амплитуда колебаний и кинетическая энергия

Кинетическая энергия математического маятника зависит от его скорости и массы. Однако амплитуда колебаний также оказывает влияние на величину кинетической энергии.

Амплитуда колебаний — это максимальное отклонение маятника от положения равновесия. Чем больше амплитуда, тем больше максимальная скорость маятника. Следовательно, кинетическая энергия маятника будет максимальной в точке с наибольшей амплитудой колебаний.

Это можно объяснить следующим образом: при большей амплитуде маятник должен пройти большее расстояние, чтобы вернуться в положение равновесия. Чтобы пройти большее расстояние за одно колебание, маятник должен двигаться быстрее. Более высокая скорость приводит к большей кинетической энергии.

Однако следует отметить, что хотя кинетическая энергия маятника максимальна в точке с наибольшей амплитудой, кинетическая энергия не остается постоянной во время колебаний. Кинетическая энергия маятника изменяется по мере его движения, достигая максимума в точке наибольшей амплитуды и минимума в точке положения равновесия.

Таким образом, амплитуда колебаний является одним из факторов, влияющих на величину кинетической энергии математического маятника. Большая амплитуда приводит к большей кинетической энергии, а меньшая амплитуда — к меньшей кинетической энергии.

Математическое выражение для кинетической энергии маятника

Кинетическая энергия математического маятника может быть выражена с помощью следующей формулы:

К = (1/2) * m * v^2

Где:

• К — кинетическая энергия маятника;
• m — масса маятника;
• v — скорость маятника.

Формула показывает, что кинетическая энергия маятника зависит от его массы и скорости. Масса маятника определяет количество энергии, которое он может накопить, а скорость маятника определяет его кинетическую энергию.

Практическое применение и выводы

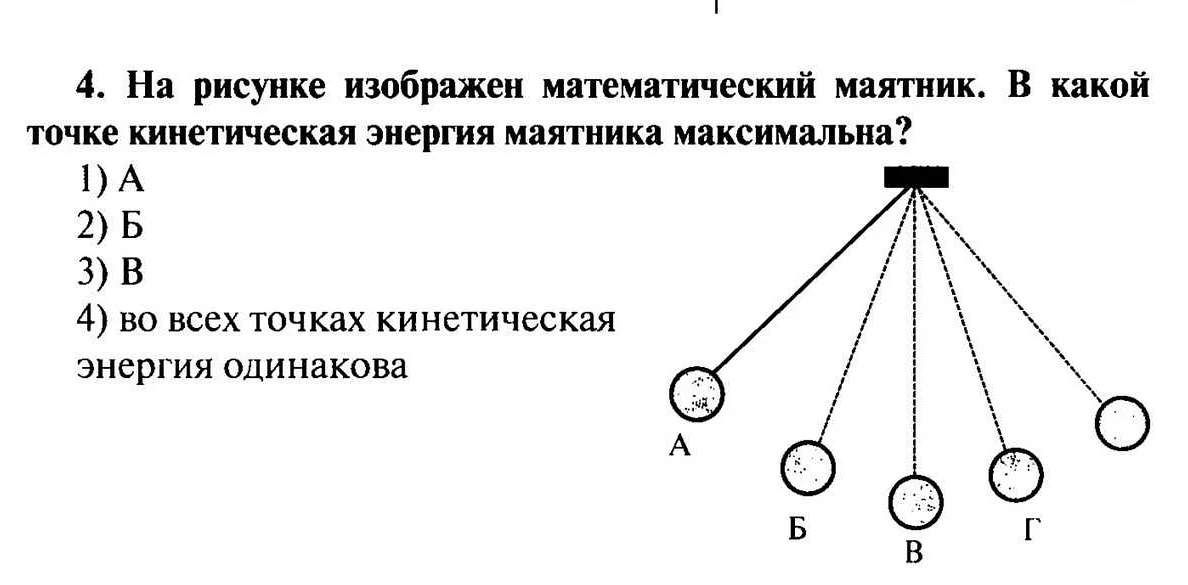
Изучение математического маятника и определение точки, в которой кинетическая энергия максимальна, имеет практическое применение в различных областях науки и техники.

Одним из примеров применения данной теории является строительство маятниковых мостов. При проектировании таких мостов необходимо учитывать точку, в которой кинетическая энергия маятника будет максимальна, чтобы обеспечить безопасность и стабильность конструкции.

Также, знание точки максимальной кинетической энергии может быть полезным при разработке механизмов с использованием маятникового движения. Например, в медицинской технике можно использовать принцип математического маятника для создания устройств, которые будут выполнять точные и ритмичные движения, например, в реабилитационных устройствах или в симуляторах хирургических операций.

Выводы, полученные в результате исследования математического маятника, могут служить основой для дальнейших научных исследований. Например, исследование влияния различных факторов на кинетическую энергию маятника может привести к разработке новых методов и технологий в области физики и инженерии.

Вопрос-ответ:

В чем заключается основной принцип работы математического маятника?

Основной принцип работы математического маятника заключается в преобразовании потенциальной энергии в кинетическую и обратно. Когда маятник отклоняется от положения равновесия, его потенциальная энергия возрастает, а кинетическая энергия уменьшается. При движении маятника в сторону положения равновесия, кинетическая энергия увеличивается, а потенциальная энергия уменьшается. Это происходит до тех пор, пока маятник не достигает максимальной скорости в положении равновесия, когда его кинетическая энергия максимальна.

В какой точке кинетическая энергия математического маятника максимальна?

Кинетическая энергия математического маятника максимальна в точке, где его скорость максимальна. Это происходит в положении равновесия, когда маятник проходит через центр своего движения. В этой точке потенциальная энергия маятника минимальна, а кинетическая энергия достигает своего максимального значения.

Каким образом можно определить, в какой точке кинетическая энергия маятника максимальна?

Для определения точки, в которой кинетическая энергия маятника максимальна, необходимо использовать закон сохранения механической энергии. Этот закон утверждает, что сумма потенциальной и кинетической энергии системы остается постоянной. Таким образом, когда потенциальная энергия маятника максимальна, кинетическая энергия будет минимальной и наоборот. Следовательно, точка, в которой кинетическая энергия максимальна, соответствует положению равновесия маятника.

Какая формула позволяет вычислить кинетическую энергию математического маятника в разных точках?

Кинетическая энергия математического маятника может быть вычислена с использованием формулы: K = (1/2) * m * v^2, где K — кинетическая энергия, m — масса маятника, v — скорость маятника. В разных точках движения маятника масса остается постоянной, поэтому скорость является определяющим фактором для определения кинетической энергии. В положении равновесия, где скорость максимальна, кинетическая энергия также будет максимальной.

Видео по теме: