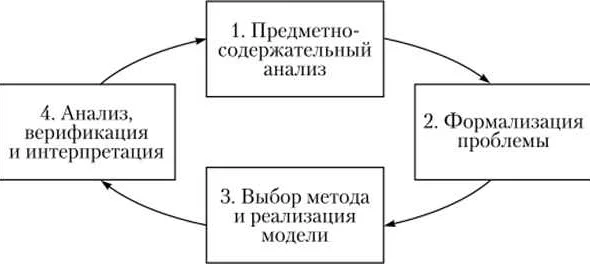
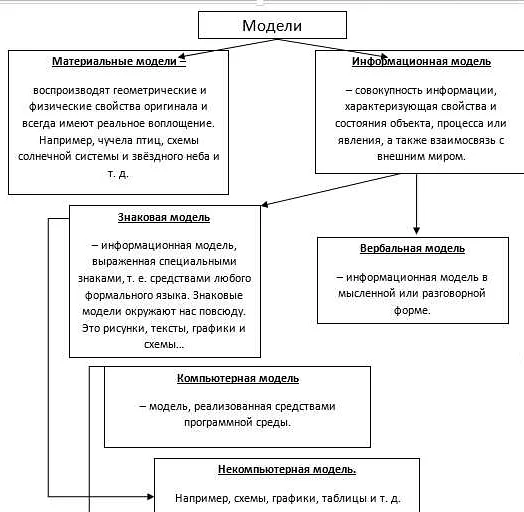
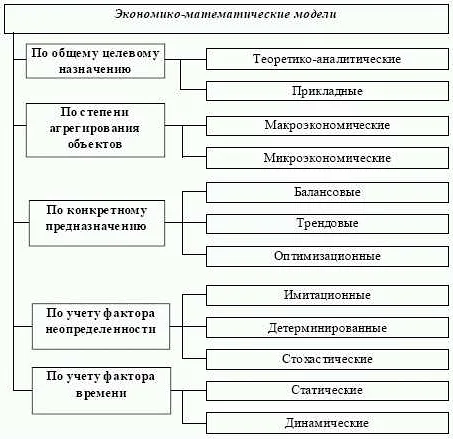
Математическое моделирование: основные понятия и принципы

Математическое моделирование – это процесс создания математических моделей для изучения реальных систем и явлений. В статье рассмотрены основные понятия и методы математического моделирования, его применение в различных областях науки и техники.

Математическое моделирование – это процесс описания реального объекта или явления в виде математической модели. Математическая модель представляет собой систему математических уравнений, которые отображают основные законы и свойства объекта или явления.

Математическое моделирование применяется во многих областях науки и техники. Оно позволяет проводить виртуальные эксперименты, оценивать вероятность возникновения определенных ситуаций и прогнозировать поведение системы в различных условиях.

Одной из основных функций математического моделирования является оптимизация процессов в различных областях. Например, математические модели позволяют улучшать производственные процессы, создавать новые материалы и технологии, сокращать расходы и повышать эффективность использования ресурсов.

Также математическое моделирование используется для прогнозирования различных явлений, таких как погода, цены на акции, поведение рынков и многих других. Это особенно важно для принятия решений в экономике и бизнесе, так как позволяет оценивать риски и прогнозировать возможные последствия.

Начало истории математического моделирования

История математического моделирования началась в глубокой древности. Один из первых математических объектов, над которыми работали люди, были числа. Именно числа позволили человеку улучшить свое понимание окружающего мира и начать его моделирование. В древних цивилизациях разработали первые математические методы, которые использовались для решения задач, связанных с обработкой земли, ее улучшением и сбором урожая.

С течением времени люди сталкивались с все более сложными и различными задачами, которые не могли быть решены простыми математическими методами. Постепенно начали развиваться методы моделирования, которые позволяли решать более сложные задачи.

Одним из первых известных примеров в области математического моделирования стало создание таблицы логарифмов английским математиком Джоном Непером в 1614 году. Эта таблица использовалась для упрощения математических вычислений. Позднее этот метод получил широкое распространение во всех областях науки, где требовалось быстро и точно решать математические задачи.

В настоящее время математическое моделирование применяется практически во всех областях науки и техники: от геологии, физики и химии, до экономики и финансов. Эти модели используются для прогнозирования различных явлений, создания новых технологий и средств коммуникации, управления ресурсами и организации бизнес-процессов.

Видео по теме:

Что такое математическая модель?

Математическая модель – это абстрактное представление реальных объектов, систем или явлений в виде математических уравнений, формул и графиков.

Создание математических моделей позволяет исследовать и предсказывать реакцию объекта на различные внешние воздействия и изменения в его состоянии.

Такие модели используются во многих сферах деятельности, включая экономику, науку, технику, медицину и многие другие.

Применение математических моделей позволяет сократить время на исследование объектов и снизить риски при принятии решений в различных ситуациях. Они также позволяют улучшить качество и эффективность различных технологий и процессов.

Одним из примеров математической модели является формула Фурье, которая используется для описания периодических функций в математике и физике.

В каких областях применяют математическое моделирование?

Математическое моделирование — это методология, которая помогает представить сложные физические и социальные процессы в виде математических моделей. Такие модели позволяют проводить исследования, прогнозировать результаты и принимать на их основе решения.

Математическое моделирование активно применяется во многих областях, например:

• Наука и технологии: моделирование физических явлений и процессов в физике, химии, биологии, информатике; моделирование сложных систем, таких как космические аппараты, летательные аппараты и многое другое.
• Экономика и финансы: моделирование экономических процессов, прогнозирование тенденций, определение секторов экономики, которые нуждаются в развитии, определение цен и многое другое.
• Социология и политика: моделирование поведения людей, принятие решений и групповых процессов; прогнозирование социальных и политических событий.
• Инженерия и производство: моделирование технических систем и процессов, оптимизация производственных процессов, управления инженерными системами и многое другое.

Можно сказать, что математическое моделирование является универсальным методом для решения различных задач, связанных с анализом сложных процессов и систем.

Примеры математического моделирования в биологии

В биологии математическое моделирование широко применяется для изучения закономерностей различных биологических процессов и явлений. Например, одним из наиболее известных примеров математического моделирования в биологии является модель генетической эволюции.

Модель генетической эволюции помогает ученым понять, как меняется генетический состав популяции в зависимости от различных факторов, таких как мутации, естественный отбор, генетический дрейф и миграция. Эта модель является основой для изучения генетической эволюции в различных областях биологии, таких как генетика, популяционная биология и систематика.

Еще одним примером математического моделирования в биологии является модель распространения инфекционных болезней. С помощью математической модели ученые могут оценить скорость распространения болезни, ее максимальную и минимальную распространенность в популяции, а также эффективность различных мер по борьбе с инфекцией (например, вакцинации).

Кроме того, математическое моделирование применяется в биологии для изучения физиологических процессов, таких как дыхание, кровообращение, рост и развитие организма, а также для разработки новых лекарственных препаратов и методов лечения различных заболеваний.

Примеры математического моделирования в физике

Физика — одна из наук, где математическое моделирование играет особенно важную роль. С помощью математических моделей ученые могут предсказывать поведение объектов и явлений в физическом мире, а также проверять свои гипотезы на практике.

Примеры математического моделирования в физике:

• Модель движения материальной точки — это одна из стандартных моделей, которую используют начальные курсы физики. С ее помощью можно описать движение материальной точки в пространстве и на плоскости, задавая параметры, такие как скорость, ускорение, силы и т.д.
• Модель движения тел в жидкостях и газах — с помощью математических методов можно описать движение жидкости и газа, а также процессы, происходящие внутри этих сред. Эта модель используется в аэродинамике, гидродинамике и других областях физики.
• Модель электромагнитных волн — с помощью математических моделей можно предсказывать распространение электромагнитных волн, таких как световые волны. Эта модель используется в оптике, радиотехнике и других областях физики.
• Модель квантовой механики — это одна из самых сложных, но и интересных моделей в физике. Она описывает поведение элементарных частиц на квантовом уровне и позволяет получать прогнозы, которые проверяются в экспериментах.

Это лишь некоторые примеры того, как математическое моделирование используется в физике. Без таких моделей многие открытия и изобретения в физике были бы невозможны.

Примеры математического моделирования в экономике

Математическое моделирование играет важную роль в экономике, позволяя прогнозировать экономические явления и принимать решения на основе анализа данных. Примерами математического моделирования в экономике могут быть:

1. Модели макроэкономики: эти модели используются для изучения экономических процессов на макроуровне, включая уровень безработицы, инфляцию, производство и потребление. С помощью этих моделей экономисты могут прогнозировать будущее экономики и оценивать эффекты различных политических решений.
2. Модели микроэкономики: эти модели используются для изучения решений индивидуальных потребителей и производителей, а также их взаимодействия на рынке. С помощью этих моделей можно определить оптимальные цены и объемы производства для компаний, а также предсказать, какие товары будут пользуются спросом у потребителей.
3. Модели финансов: эти модели используются для прогнозирования изменений на финансовых рынках, оценки рисков и принятия решений об инвестировании и управлении портфелем. С помощью этих моделей можно также анализировать структуру доходности и определить рыночную стоимость финансовых инструментов.
4. Модели оптимизации: эти модели используются для определения наилучшего решения в условиях ограничений, например, выбор оптимального плана производства, распределение ресурсов или определение оптимальной стратегии инвестирования.

Это лишь некоторые примеры математического моделирования в экономике. С помощью моделирования экономисты могут учитывать множество переменных и предсказывать результаты экономических решений с большой точностью. Это помогает улучшать управление компанией, выявлять новые направления развития и принимать обоснованные решения на основе фактов и анализа данных.

Примеры математического моделирования в информатике

Математическое моделирование является неотъемлемой частью информатики, ведь это позволяет научиться создавать алгоритмы для решения различных задач.

Один из примеров математического моделирования в информатике – это создание модели алгоритма шифрования информации. При использовании алгоритма RSA, для шифрования данных используется комбинация простых чисел и математических операций с ними. На основе данной модели, разработчики создают программы для шифрования данных.

Еще один пример – это моделирование процесса передачи информации в компьютерных сетях. Разработчики создают модели каналов связи и алгоритмов обработки информации, что позволяет им предоставить стабильный и качественный сервис.

Также, математическое моделирование используется для создания программ для оптимизации производственных процессов. Путем создания математических моделей и анализа данных, разработчик может создать программу, которая позволяет более эффективно использовать ресурсы и повысить производительность производства.

В современном мире, математическое моделирование используется во многих отраслях: в авиации, медицине, финансах и других. Это показывает важность данного процесса для развития нашей жизни и науки.

Примеры математического моделирования в инженерии

Практически все современные инженерные решения базируются на применении математического моделирования. Например, при проектировании механизмов и машин, инженеры широко используют метод конечных элементов для расчета напряженно-деформированного состояния деталей в условиях эксплуатации. Это позволяет оценить прочность материалов и выбрать оптимальный дизайн.

Еще одним примером математического моделирования в инженерии является разработка проектов зданий и сооружений. Инженеры используют специализированные программы, которые позволяют проводить расчеты прочности конструкций, определять оптимальный материал для строительства и оценивать воздействие внешних нагрузок, в том числе сейсмических.

Также математическое моделирование широко применяется в автомобилестроении. Например, при проектировании двигателей и механизмов передачи инженеры используют программы, которые позволяют моделировать течение газов в цилиндрах, проводить расчеты топливной эффективности и оптимизировать параметры конструкции.

Инженеры также используют математическое моделирование для проектирования систем управления энергетическими и технологическими процессами. При этом моделируются технические системы комплексной автоматизации, с использованием систем дискретной и аналоговой автоматики. Большой интерес представляет математическое моделирование нестационарных процессов с использованием динамических моделей и компьютерных симуляторов.

Какие инструменты используются для математического моделирования?

Для математического моделирования используют различные инструменты, которые облегчают и ускоряют процесс создания модели и анализа ее результатов. Рассмотрим некоторые из них:

• Математические пакеты – это программы, которые позволяют создавать математические модели, решать уравнения и графически визуализировать результаты. К таким пакетам относятся, например, MATLAB, Maple и Mathematica;
• Языки программирования – в эту категорию входят языки программирования, предназначенные для решения задач математического моделирования. Например, такие языки как Python и R используются для математического моделирования, а также для анализа данных и машинного обучения;
• Специализированные программы – это программы, предназначенные для решения конкретных математических задач. Они позволяют работать с большими объемами данных и решать сложные задачи. К таким программам относятся, например, COMSOL, ANSYS и OpenFoam;
• Среды математического моделирования – это программные средства, предназначенные для разработки уравнений, создания моделей и анализа результатов. К таким средам относятся, например, LMS Imagine Lab Amesim и Simulink от MathWorks;
• Различные пакеты и библиотеки – это программы, которые содержат наборы функций и методов для решения конкретных задач в математическом моделировании. Например, NumPy и SciPy для языка Python предоставляют инструменты для численного решения уравнений и работы с матрицами.

Использование различных инструментов для математического моделирования позволяет создавать более точные и сложные модели, а также ускоряет и упрощает процесс их создания.

Какие результаты можно получить с помощью математического моделирования?

Одним из основных результатов математического моделирования является возможность эффективного решения сложных проблем и принятия решений на основе анализа полученных данных. С помощью математических моделей можно предсказывать поведение системы на основе различных переменных и условий.

Например, в медицине математическое моделирование используется для разработки новых лекарственных препаратов и оценки их эффективности, а также для прогнозирования распространения заболеваний и разработки планов их лечения.

В производственных и инженерных отраслях математическое моделирование позволяет оптимизировать процессы производства, предотвращать поломки оборудования и минимизировать затраты на производство.

В экономике математическое моделирование используется для анализа и прогнозирования финансовых рынков, определения оптимальной стратегии инвестирования и оценки эффекта от различных экономических реформ.

Другим важным результатом математического моделирования является возможность проведения виртуальных экспериментов и тестирования. Это позволяет сократить время и затраты на реальных тестах и уменьшить риски для жизни и здоровья людей.

Таким образом, математическое моделирование является мощным инструментом, позволяющим получать точные и достоверные данные, на основе которых можно принимать обоснованные и эффективные решения в различных областях деятельности.

Вопрос-ответ:

Что такое математическое моделирование и зачем оно нужно?

Математическое моделирование — это процесс создания математических моделей, которые описывают поведение реальных объектов и систем. Эти модели позволяют предсказывать, как будет вести себя система в различных условиях, и оптимизировать ее работу. Оно нужно многим отраслям, включая науку, инженерию, экономику и медицину, и может использоваться для решения широкого круга задач, таких как разработка новых продуктов, оптимизация производственных процессов, прогнозирование погоды, разработка лекарств и т.д.

Какие методы используют для математического моделирования?

Существует множество методов и подходов к математическому моделированию, таких как дифференциальные уравнения, статистические методы, методы оптимизации и т.д. Но в общем виде процесс моделирования выглядит так: сначала анализируются данные, описывающие систему, затем строится математическая модель, которая описывает это поведение, и наконец модель проверяется и актуализируется на основе полученных результатов.

Может ли математическое моделирование принести вред, если оно будет неправильно выполнено?

Да, неправильно выполненное математическое моделирование может привести к ошибочным выводам и неправильным решениям. Поэтому очень важно правильно выбирать методы моделирования, знать характеристики объекта моделирования и обрабатывать данные правильно. Важную роль играют также опыт и профессионализм модельеров, а также тщательная проверка и валидация модели.

Где и как применяется математическое моделирование?

Моделирование применяется во многих отраслях: в науке, технике, экономике, медицине, биологии и др. Оно используется для прогнозирования и оптимизации процессов и явлений, создания новых продуктов и технологий, улучшения качества жизни, решения социально-экономических задач и др. Это бесценный инструмент для научных и инженерных исследований, а на практике его применение может значительно сократить расходы и сократить время на проектирование и разработку новых систем.

На сколько сложно научиться математическому моделированию?

Для того, чтобы научиться математическому моделированию, необходимо обладать знаниями в области математики, программирования и статистики. Но главным для успешного моделирования является понимание основных принципов, а также опыт в решении практических задач. Сложность зависит от уровня задачи и выбранного метода моделирования, но в целом для обучения основам может потребоваться несколько месяцев до года обучения.

Какие преимущества может дать математическое моделирование в бизнесе?

Математическое моделирование может привнести в бизнес значительный экономический эффект, так как оно позволяет оптимизировать существующие процессы и убедиться в правильности решения бизнес-задач. Например, можно использовать моделирование для оптимизации логистики, чтобы более эффективно использовать ресурсы, уменьшить затраты на транспортировку и т.д. Более сложные модели могут применяться для прогнозирования спроса, оптимизации ценообразования, анализа рисков, управления финансами и т.д.

Какие особенности используют при создании математических моделей в экономике?

В экономике при создании математических моделей используются специальные методы, которые учитывают специфику данной отрасли и ее законы. Экономические модели могут быть детерминистическими или стохастическими, что зависит от того, насколько точно можно описать процессы, которые проходят в экономической системе. Модели экономики также могут быть разделены на микроэкономические и макроэкономические, в зависимости от того, насколько они описывают мелкие компоненты экономики, такие как производство и потребление, или же более общие явления, такие как инфляция, безработица и т.д.