Какой примерно период колебаний математического маятника длиной 40 м

Узнайте, какой будет примерно период колебаний математического маятника с длиной 40 метров. Изучите основные принципы и формулы, чтобы рассчитать период колебаний для любой длины маятника.

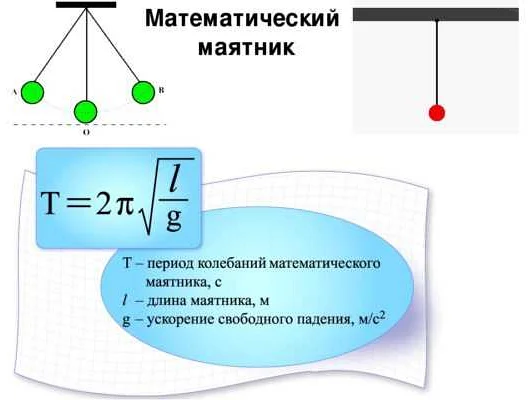
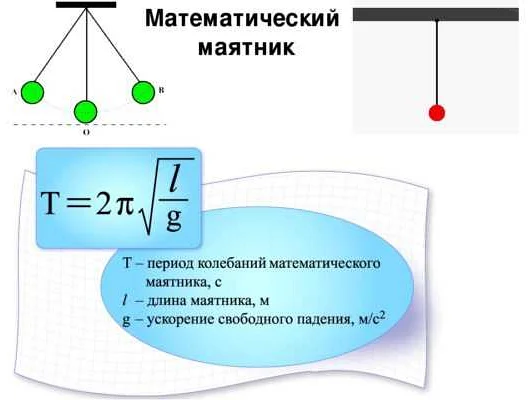
Математический маятник – это простейшая модель колебательного движения, которая состоит из невесомой нити и точки, называемой массой. Длина этой нити и масса определяют период колебаний маятника. Период колебаний – это время, за которое маятник совершает одну полную колебательную волну, начиная с одного крайнего положения и возвращаясь в него же.

В нашей статье рассмотрим математический маятник длиной 40 метров. Для расчета периода колебаний такого маятника используется формула, которая основана на законах механики и гравитации.

Период колебаний T математического маятника можно вычислить по формуле:

T = 2π√(L/g)

где L – длина нити маятника в метрах, а g – ускорение свободного падения, примерное значение которого на Земле составляет около 9,8 м/с².

Используя данную формулу, можно легко рассчитать период колебаний математического маятника длиной 40 метров и получить точное значение времени, за которое маятник совершит одну полную колебательную волну.

Что такое математический маятник

Математический маятник является одним из классических примеров системы с гармоническими колебаниями. Он представляет собой систему, в которой масса точечного тела движется в горизонтальной плоскости под действием силы тяжести и упругой силы, возникающей из-за изгиба стержня.

Основные параметры математического маятника — длина стержня и масса точечной массы. При изменении этих параметров меняется период колебаний маятника. Длина стержня определяет скорость периодических колебаний, а масса точки влияет на инерцию системы.

Математический маятник широко используется в научных и образовательных целях. Он является моделью для исследования колебаний различных физических систем, таких как маятники в часах, маятники в физических лабораториях и другие системы, обладающие схожими свойствами.

ПараметрЗначение

Длина стержня

40 м

Описание и принцип работы

Принцип работы математического маятника основан на законах механики и гравитации. Когда маятник отклоняется от положения равновесия и отпускается, на него начинает действовать сила тяжести, которая направлена вниз и стремится вернуть маятник в положение равновесия. За счет инерции тела, маятник движется в противоположную сторону от отклонения и затем возвращается обратно. Этот процесс повторяется до тех пор, пока не происходит затухание колебаний.

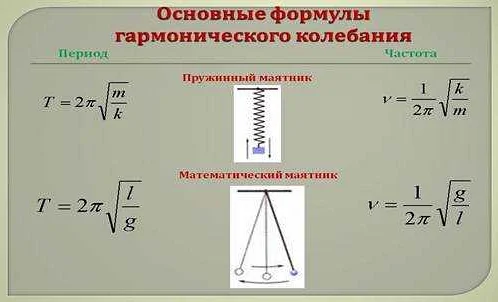
Период колебаний математического маятника зависит от его длины и ускорения свободного падения. Длина маятника и ускорение свободного падения взаимосвязаны формулой:

T = 2π * √(l / g),

где T – период колебаний, l – длина маятника, g – ускорение свободного падения.

Формула для расчета периода колебаний

Период колебаний математического маятника зависит от его длины. Для расчета периода колебаний используется следующая формула:

Т = 2π√(L/g)

Где:

• Т — период колебаний (в секундах);
• π — математическая константа, примерное значение равно 3.14;
• L — длина маятника (в метрах);
• g — ускорение свободного падения (приближенное значение равно 9.8 м/с²).

С помощью данной формулы можно рассчитать период колебаний математического маятника, если известны его длина и ускорение свободного падения.

Формула и ее составляющие

Период колебаний математического маятника длиной 40 м может быть рассчитан с помощью соответствующей формулы. Формула для расчета периода колебаний математического маятника выглядит следующим образом:

Т = 2π√(L/g),

где:

• Т — период колебаний,
• π — математическая константа, примерно равная 3.14159,
• L — длина маятника,
• g — ускорение свободного падения, примерно равное 9.8 м/с².

Формула позволяет рассчитать период колебаний для математического маятника с заданной длиной. Для расчета необходимо знать длину маятника и ускорение свободного падения.

Расчет периода колебаний математического маятника длиной 40 м

Период колебаний математического маятника зависит от его длины. Для расчета периода колебаний математического маятника длиной 40 м необходимо использовать формулу:

Т = 2π√(l/g)

Где:

• Т — период колебаний (в секундах)
• π — математическая константа, примерно равная 3.14159
• l — длина маятника (в метрах)
• g — ускорение свободного падения (приближенное значение 9.8 м/с²)

Подставляя значения в формулу, получаем:

Т = 2π√(40/9.8)

Расчитаем:

• Т = 2 * 3.14159 * √(40/9.8) ≈ 6.28318 * √(4.08163) ≈ 6.28318 * 2.02059 ≈ 12.69494 секунды

Таким образом, период колебаний математического маятника длиной 40 м составляет примерно 12.69494 секунды.

Учет длины маятника и гравитационной постоянной

Формула для расчета периода колебаний математического маятника имеет вид:

где T — период колебаний, L — длина маятника, g — гравитационная постоянная.

Гравитационная постоянная (g) представляет собой ускорение свободного падения и примерно равна 9,8 м/с² на поверхности Земли. Однако, для более точных расчетов, значение g может варьироваться в зависимости от конкретных условий и местоположения.

Таким образом, учет длины маятника и гравитационной постоянной позволяет более точно определить период колебаний математического маятника и использовать эту информацию для решения различных задач и проблем. Важно помнить, что формула может быть применена только для малых колебаний маятника и не учитывает влияние воздушного сопротивления и других факторов.

Особенности и применение математического маятника

Одна из особенностей математического маятника заключается в том, что его период колебаний зависит только от длины стержня и ускорения свободного падения. Это означает, что при одинаковой длине маятник будет колебаться с одинаковой частотой, независимо от массы точечной массы или начального отклонения.

Математический маятник широко используется в научных исследованиях, в образовательных целях, а также в различных технических областях. Он применяется для определения ускорения свободного падения, изучения законов сохранения энергии и момента импульса, а также для измерения времени и создания точных механических часов.

Кроме того, математический маятник находит применение в астрономии и геодезии. Он используется для измерения гравитационного ускорения на разных широтах Земли и для определения географической широты места.

Таким образом, математический маятник представляет собой важный инструмент для изучения колебаний и основных законов механики. Его применение находит широкое применение в науке, образовании и технике, а также в геодезии и астрономии.

Применение в научных и практических областях

В науке математический маятник используется для изучения основных закономерностей колебательных процессов. Он является одной из простейших систем и позволяет исследовать такие важные понятия, как период колебаний, амплитуда, длина маятника и зависимость периода от этих параметров. Эти исследования позволяют лучше понять природу колебательных процессов и применить полученные знания в различных областях научных исследований.

В практике математический маятник находит применение в различных областях. Он используется, например, в метрологии для калибровки и проверки точности измерительных приборов. Благодаря своей простоте и стабильности, математический маятник позволяет получить точные и повторяемые измерения времени и частоты. Это особенно важно в таких областях, как физика, механика, электроника и промышленное производство, где требуется высокая точность и надежность измерений.

Кроме того, математический маятник находит применение в различных инженерных задачах. Например, он может быть использован для расчета периода колебаний маятниковых механизмов или для определения оптимальной длины подвеса в различных конструкциях. Эти расчеты позволяют проектировать более эффективные и устойчивые системы, а также предсказывать их поведение в различных условиях.

Видео по теме:

Вопрос-ответ:

Как рассчитать период колебаний математического маятника длиной 40 м?

Период колебаний математического маятника можно рассчитать с помощью формулы T = 2π√(L/g), где T — период колебаний, L — длина маятника, g — ускорение свободного падения. Для маятника длиной 40 м формула примет вид T = 2π√(40/9.8), что можно упростить до T ≈ 12.84 секунды.

Какая формула используется для расчета периода колебаний математического маятника?

Формула для расчета периода колебаний математического маятника имеет вид T = 2π√(L/g), где T — период колебаний, L — длина маятника, g — ускорение свободного падения. Эта формула позволяет определить, сколько времени займут одно полное колебание маятника.

Каков период колебаний математического маятника длиной 40 м?

Период колебаний математического маятника длиной 40 м составляет примерно 12.84 секунды. Это означает, что маятник совершит одно полное колебание в течение 12.84 секунд.

Как влияет длина математического маятника на его период колебаний?

Длина математического маятника напрямую влияет на его период колебаний. Согласно формуле T = 2π√(L/g), где T — период колебаний, L — длина маятника, g — ускорение свободного падения, чем длиннее маятник, тем больше будет его период колебаний. То есть, чем длиннее маятник, тем больше времени потребуется для совершения одного полного колебания.

Какое ускорение свободного падения используется при расчете периода колебаний математического маятника длиной 40 м?

При расчете периода колебаний математического маятника длиной 40 м используется ускорение свободного падения, равное примерно 9.8 м/с². Это стандартное значение, используемое в физических расчетах, и оно позволяет получить более точные результаты при определении периода колебаний маятника.

Как рассчитать период колебаний математического маятника длиной 40 м?

Период колебаний математического маятника можно рассчитать с помощью формулы T = 2π√(L/g), где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

Факторы, влияющие на период колебаний

Период колебаний математического маятника может быть подвержен влиянию различных факторов, которые могут изменять его продолжительность. Некоторые из этих факторов включают:

• Длина маятника: Зависимость периода колебаний от длины маятника является одной из основных особенностей математического маятника. Чем длиннее маятник, тем медленнее будет происходить его колебание.
• Сила тяжести: Ускорение свободного падения, которое определяется силой тяжести, также влияет на период колебаний. В районах с разной силой тяжести периоды колебаний могут отличаться.
• Масса маятника: Масса маятника также может повлиять на период колебаний. Чем больше масса маятника, тем медленнее будет происходить его колебание.
• Амплитуда колебаний: Амплитуда колебаний, то есть максимальное отклонение маятника от положения равновесия, также влияет на период колебаний. Большая амплитуда может увеличить период, а маленькая — сократить его.
• Сопротивление среды: Если маятник колеблется в среде с сопротивлением, таком как воздух или вода, это также может влиять на его период колебаний. Сопротивление среды может замедлить период колебаний.

Учитывая эти факторы, можно проводить расчеты и использовать соответствующую формулу для определения периода колебаний математического маятника.

Масса маятника и сила трения

Сила трения также влияет на период колебаний математического маятника. При наличии силы трения, период колебаний будет увеличиваться. Сила трения возникает в результате взаимодействия маятника с воздухом или другими средами. Чем больше сила трения, тем сильнее будет замедляться движение маятника и тем больше будет его период колебаний.

Изменение массы маятника или силы трения может привести к изменению периода колебаний. Поэтому при расчете периода колебаний математического маятника необходимо учитывать эти параметры.