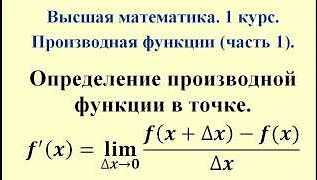Что такое производная в математике для чайников

Производная в математике – это понятие, которое позволяет изучать скорость изменения функции в каждой точке. В этой статье вы узнаете, как определить производную, какие основные правила дифференцирования существуют и как использовать производные в решении задач.

Производная — одно из важнейших понятий в математике, которое позволяет изучать функции и их изменения. Она используется в различных областях науки и техники, таких как физика, экономика, биология и многих других. Понимание производной поможет вам решать задачи и анализировать поведение функций.

Производная функции определяет скорость изменения значения функции в каждой ее точке. Она может быть представлена как отношение приращения функции к приращению ее аргумента. Вот как это записывается:

Производная функции f(x) обозначается как f'(x) или dy/dx.

Производная может быть положительной, отрицательной или равной нулю в зависимости от поведения функции. Если производная функции положительна, это означает, что функция возрастает. Если производная отрицательна, то функция убывает. Если производная равна нулю, то функция имеет экстремум, то есть максимум или минимум.

Важно отметить, что производная является основой для построения теории дифференциального исчисления. Она позволяет найти точку максимума или минимума функции, а также определить ее выпуклость и вогнутость. Знание производной позволяет анализировать функции и решать множество задач в различных областях знания.

Зачем нужна производная?

С помощью производной мы можем определить скорость изменения функции в каждой ее точке. Она показывает, как быстро меняется значение функции при изменении ее аргумента. Например, если мы рассматриваем функцию, описывающую движение объекта, производная позволяет нам определить, с какой скоростью объект движется в данный момент времени.

Также производная позволяет нам находить точки экстремума функции – максимумы и минимумы. Это полезно, например, при оптимизации процессов в экономике или при поиске наилучшего решения в задачах оптимизации.

Производная также используется для аппроксимации функций. Мы можем приблизить сложную функцию с помощью ее производной и использовать эту аппроксимацию для упрощения вычислений или аналитического решения задачи.

Кроме того, производная является основой для понимания интеграла, который является обратной операцией к дифференцированию и позволяет нам находить площади, объемы и другие величины. Таким образом, производная и интеграл тесно связаны и составляют фундаментальные понятия математического анализа.

Как вычислить производную?

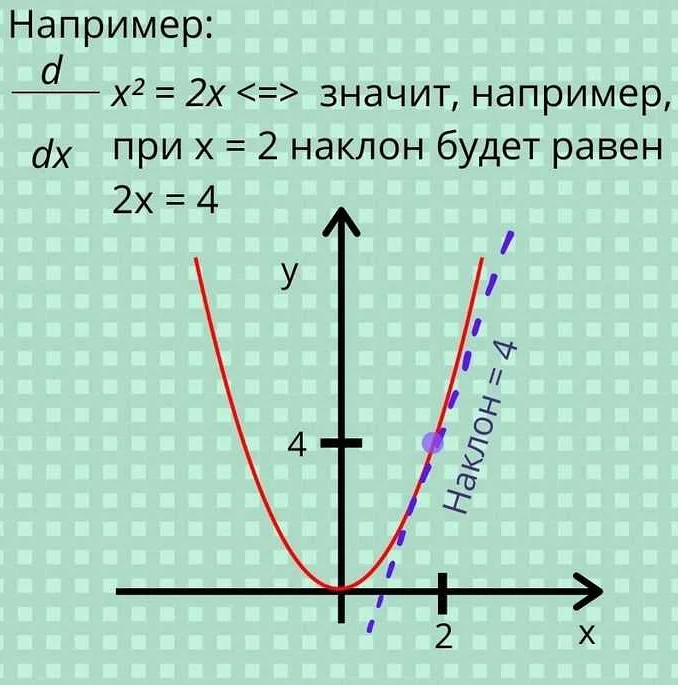
Для вычисления производной функции существует несколько методов, включая прямое дифференцирование, использование формул дифференцирования и правило Лейбница. В основе всех этих методов лежит понятие предела, которое позволяет нам определить скорость изменения функции в определенной точке.

Прямое дифференцирование является наиболее простым методом вычисления производной. Он основан на использовании определения производной как предела отношения приращения функции к приращению аргумента при стремлении последнего к нулю. Формула для вычисления производной в этом случае просто записывается как отношение приращения функции к приращению аргумента и вычисляется аналитически.

Использование формул дифференцирования позволяет нам вычислить производную функции, используя известные правила и свойства производных. Например, для функций вида f(x) = xn, где n — целое число, существуют формулы дифференцирования, которые позволяют нам выразить производную в явном виде.

Правило Лейбница является общим методом дифференцирования, который позволяет вычислить производную сложной функции, используя производные составляющих функций. Оно основано на умножении производных функций и суммировании результатов.

Вычисление производной может быть сложным процессом, особенно для сложных функций. Однако, с помощью правил дифференцирования и некоторой практики, вы можете научиться эффективно вычислять производные и применять их в различных задачах.

Правила дифференцирования

Основные правила дифференцирования:

1. Правило линейности: производная суммы двух функций равна сумме их производных.
2. Правило произведения: производная произведения двух функций равна произведению производной первой функции и второй функции, плюс произведение первой функции и производной второй функции.
3. Правило частного: производная частного двух функций равна разности произведения производной первой функции и второй функции, минус произведение первой функции и производной второй функции, деленное на квадрат второй функции.
4. Правило степени: производная функции в степени равна произведению степени, коэффициента и производной самой функции в степени минус один.
5. Правило суммы: производная суммы функций равна сумме их производных.

Это лишь некоторые из основных правил дифференцирования. С их помощью можно находить производные более сложных функций и решать разнообразные задачи в математике и физике.

Примеры вычисления производных

Рассмотрим несколько примеров вычисления производных:

Пример 1:

Функция: f(x) = 3×2 + 2x — 1

Чтобы найти производную этой функции, нужно взять производную каждого слагаемого по отдельности и суммировать результаты. Производная константы равна нулю. Производная x равна 1. Производная x2 равна 2x. Таким образом:

f'(x) = 2(3×2) + 1(2x) + 0 = 6x + 2

Пример 2:

Функция: g(x) = 5sin(x) + 3cos(x)

Для вычисления производной сложной функции, нужно применить правило дифференцирования сложной функции. Производная синуса равна косинусу, а производная косинуса равна минус синусу. Таким образом:

g'(x) = 5cos(x) — 3sin(x)

Пример 3:

Функция: h(x) = ln(x2)

Для вычисления производной логарифма, нужно использовать правило дифференцирования логарифма. Производная логарифма от аргумента равна производной аргумента, деленной на аргумент. Таким образом:

h'(x) = (2x/x2) = 2/x

Это лишь некоторые примеры вычисления производных. Производные играют важную роль во многих областях математики и физики, и их понимание позволяет более глубоко изучать функции и их свойства.

Производная как скорость изменения

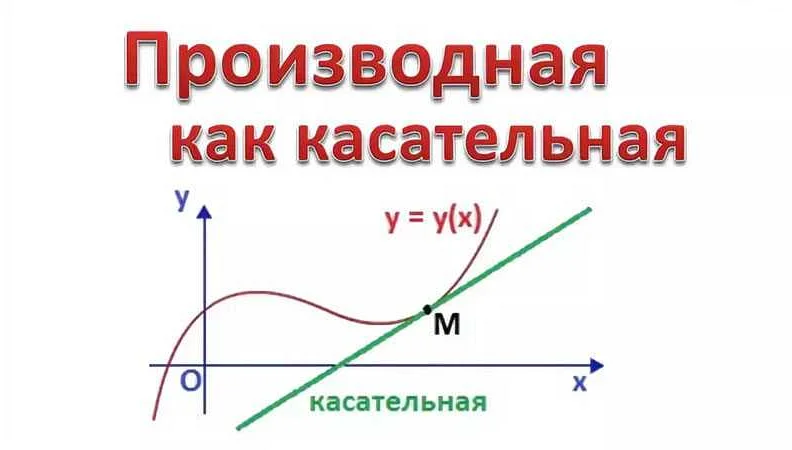
Чтобы лучше понять, что такое производная как скорость изменения, рассмотрим простой пример. Представим себе автомобиль, который движется по дороге. Мы можем измерить его скорость в определенный момент времени. Однако, нам также интересно узнать, как быстро меняется скорость автомобиля по отношению к времени.

Аналогично, в математике мы можем рассмотреть функцию и ее изменение. Производная позволяет нам изучать скорость изменения этой функции. Если функция представляет график зависимости какой-либо величины от другой (например, расстояния от времени), то производная покажет, насколько быстро меняется эта величина при изменении аргумента (скорость изменения).

Производная функции обозначается символом f’ или dy/dx, где y — значение функции, а x — аргумент (независимая переменная).

Зная производную функции, мы можем определить, в какой точке графика функции значение наиболее быстро меняется (точка экстремума), а также изучать различные характеристики функции, например, выпуклость и вогнутость.

Применение производной в задачах

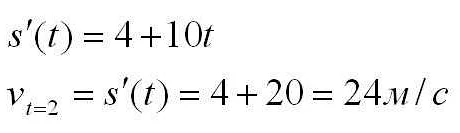
Применение производной в задачах позволяет решать такие задачи, как оптимизация функций, нахождение экстремумов, а также анализ и предсказание поведения графиков функций.

Одним из самых распространенных применений производной является нахождение критических точек и точек экстремума функции. Производная позволяет найти точки, в которых функция достигает своего максимального или минимального значения. Это особенно полезно при решении задач на оптимизацию, например, при нахождении наибольшей или наименьшей площади фигуры при заданных условиях.

Производная также используется для анализа поведения функции в окрестности ее точек. Знак производной позволяет определить возрастание или убывание функции, а экстремумы функции могут указывать на переход между возрастанием и убыванием. Это позволяет предсказывать поведение графика функции и делать выводы о ее свойствах, таких как выпуклость или вогнутость.

Важно отметить, что применение производной в задачах требует не только математических навыков, но и умение интерпретировать результаты в контексте задачи. Грамотное использование производной позволяет решить множество задач и упростить анализ функций в различных областях науки и техники.

Вопрос-ответ:

Что такое производная?

Производная — это основной инструмент дифференциального исчисления, который позволяет находить скорость изменения функции в каждой точке ее графика.

Зачем нужна производная?

Производная является важным инструментом для анализа и изучения функций. Она помогает определить экстремумы, т.е. точки максимума или минимума функции, а также позволяет решать различные задачи, связанные с изменением величин.

Как вычислить производную функции?

Чтобы вычислить производную функции, необходимо применить определенные правила дифференцирования. Например, для функции вида f(x) = x^n, производная равна n*x^(n-1), где n — степень функции.

Какие есть основные правила дифференцирования?

Основные правила дифференцирования включают правила линейности, правило дифференцирования суммы, правило дифференцирования произведения, правило дифференцирования частного и правило дифференцирования сложной функции (правило цепочки).

Чему равна производная константы?

Производная константы равна нулю, так как константа не изменяется в зависимости от переменной.

Что такое производная?

Производная функции — это понятие в математике, которое показывает, как меняется значение функции при изменении ее аргумента. Можно сказать, что производная показывает скорость изменения функции.

Видео по теме: