Что такое пропорции в математике 7 класс
Содержимое
- 1 Что такое пропорции в математике 7 класс
- 1.1 Что такое пропорции в математике
- 1.2 Видео по теме:
- 1.3 Основные понятия
- 1.4 Пропорциональность
- 1.5 Вопрос-ответ:
- 1.6 Пропорциональные отношения
- 1.7 Примеры пропорций
- 1.8 Пример 1: Расчет площади прямоугольника
- 1.9 Пример 2: Расчет времени пути
- 1.10 Практическое применение пропорций
- 1.11 Строительство
- 1.12 Финансы
Пропорции в математике 7 класс – это основа для понимания соотношений и пропорциональных зависимостей между числами и величинами. Узнайте, как решать задачи на пропорции и применять их в реальной жизни.
Пропорция – это математическое понятие, которое встречается не только в школьной программе, но и в различных сферах жизни. Пропорции позволяют сравнивать величины и устанавливать между ними соотношения. В 7 классе ученики начинают изучать основы пропорций и их применение.
Основное правило пропорции: четыре числа образуют пропорцию, если и только если их отношение равно. Например, если a:b = c:d, то говорят, что числа a, b, c и d образуют пропорцию. Также можно записать это в виде a/b = c/d. При этом a и d называются крайними членами, а b и c – средними членами пропорции.
Пропорции широко используются в реальной жизни. Например, они помогают решать задачи по смешиванию ингредиентов при готовке, расчете скидок и наценок при покупках, а также в архитектуре и дизайне при создании пропорций объектов.
Для решения задач на пропорции в 7 классе используются различные методы, один из которых – крестовый метод. Он основан на равенстве произведений крайних и средних членов пропорции. Этот метод позволяет находить неизвестные значения в пропорции и решать разнообразные задачи.
Что такое пропорции в математике

Пропорция состоит из четырех величин, которые связаны между собой отношениями. Обычно пропорция представляется в виде таблицы, где каждая строчка соответствует одной величине, а столбцы содержат значения этих величин.
| Величина A | Величина B |
| Величина C | Величина D |
Пропорция обозначается символом «:», например, A:B = C:D. При этом величины A и D называются крайними членами пропорции, а величины B и C — средними членами.
Одна из основных свойств пропорции заключается в том, что произведение крайних членов всегда равно произведению средних членов, то есть A * D = B * C.
Пропорции широко используются в различных областях, таких как физика, экономика, геометрия и т.д. Они позволяют устанавливать соотношения между различными величинами и предсказывать результаты на основе имеющихся данных.
Видео по теме:
Основные понятия

В пропорции участвуют четыре числа, которые называются членами пропорции. Члены пропорции делятся на две пары: первая пара состоит из первого и второго членов, а вторая пара — из третьего и четвертого членов.
Пропорция записывается с помощью символа «:», так что для пропорции A:B::C:D можно написать A/B = C/D.
Для решения задач на пропорции используется свойство равенства произведений крест-на-крест. Если пропорция A:B::C:D верна, то можно написать A * D = B * C.
Пропорции часто используются в жизни и в различных областях, таких как финансы, наука, архитектура и технические науки.
Пропорциональность
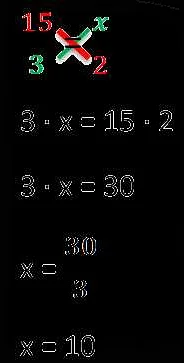
Пропорциональность — это особый вид отношения между величинами, когда они связаны пропорцией. Если две или несколько величин пропорциональны, то изменение одной величины приводит к изменению другой величины в определенной пропорциональности. Пропорциональность может быть прямой (значения величин растут или убывают одновременно) или обратной (значения величин изменяются в противоположных направлениях).
Чтобы определить, являются ли две величины пропорциональными, можно построить таблицу значений и проверить, сохраняется ли отношение между ними. Если отношение между значениями остается постоянным, то величины пропорциональны.
Пропорциональность широко используется в различных областях, таких как физика, экономика и геометрия. Знание пропорциональности позволяет решать разнообразные задачи, связанные с расчетами и сравнениями величин.
Величина AВеличина BОтношение A/B
| 2 | 4 | 1/2 |
| 5 | 10 | 1/2 |
| 8 | 16 | 1/2 |
В приведенной таблице видно, что отношение между величинами A и B всегда равно 1/2. Поэтому величины A и B являются пропорциональными.
Вопрос-ответ:
Что такое пропорция в математике?
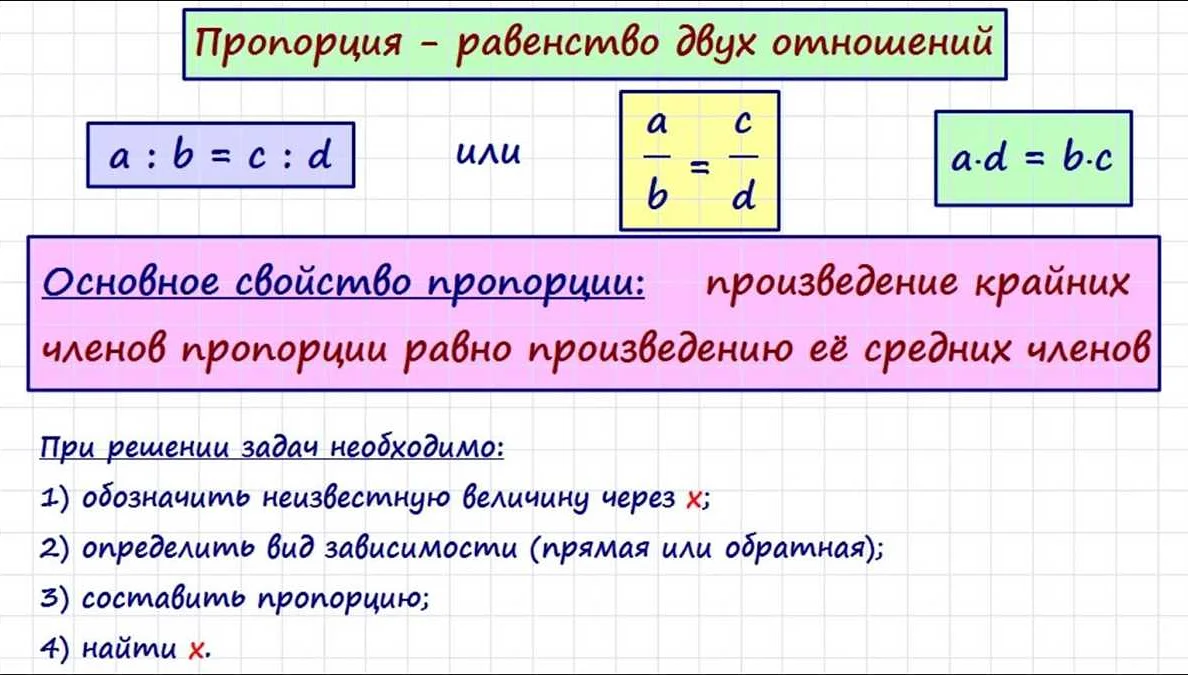
Пропорция — это равенство двух отношений. В пропорции сравниваются две пары чисел или величин. Обычно записывается в виде a:b = c:d, где a, b, c, d — числа или величины.
Как проверить, является ли пропорция верной?
Если в пропорции a:b = c:d отношения a/b и c/d равны между собой, то пропорция верна. Для проверки можно вычислить значение каждого отношения и сравнить их.
Как решить задачу на пропорцию?
Для решения задачи на пропорцию нужно сначала записать известные данные в виде пропорции, затем найти неизвестное значение, применяя свойство равенства пропорций. Полученное значение будет ответом на задачу.
Как применять пропорции на практике?
Пропорции широко используются в различных сферах жизни: в строительстве, финансах, рецептах, картографии и т.д. Они помогают сравнивать и пропорционально изменять различные величины и значения.
Какие свойства имеют пропорции?
Пропорции обладают следующими свойствами: свойство перестановки, свойство сокращения, свойство умножения и свойство деления. Эти свойства позволяют упрощать выражения и решать задачи на пропорции более эффективно.
Какие основные понятия связаны с пропорциями в математике?
Основные понятия, связанные с пропорциями, включают: пропорциональность, пропорционность чисел, пропорциональность отрезков, пропорциональность площадей и т.д.
Пропорциональные отношения
Пропорциональные отношения можно представить в виде дроби, где числитель и знаменатель обозначают соответствующие значения двух величин. Например, если две величины A и B пропорциональны, то их отношение может быть записано как A/B или B/A.
Пропорциональные отношения часто используются для решения задач, связанных с пропорциями. В таких задачах известны значения нескольких величин, и требуется найти значение некоторой другой величины, используя пропорцию между ними.
Пропорциональные отношения также могут быть представлены в виде таблицы или графика, что облегчает визуализацию и анализ связей между величинами.
Примеры пропорциональных отношений могут включать такие понятия, как скорость и время, расстояние и время, объем и масса и др.
Важно помнить, что пропорциональные отношения могут быть прямыми (когда увеличение одной величины приводит к увеличению другой) или обратными (когда увеличение одной величины приводит к уменьшению другой).
Понимание пропорциональных отношений играет важную роль в решении задач по математике и в реальных ситуациях, где требуется анализ и сравнение различных величин.
Примеры пропорций
Рассмотрим несколько примеров пропорций:
-
- Пример 1: Если 5 яблок стоят 200 рублей, то сколько стоят 10 яблок?
Решение: Здесь мы можем записать пропорцию: 5/200 = 10/x.
Чтобы найти значение x, нужно умножить 10 на 200 и поделить на 5. Получаем x = 400 рублей.
-
- Пример 2: В пропорции 3/4 = x/12 найти значение x.
Решение: Мы можем умножить 3 на 12 и поделить на 4, чтобы найти значение x. Получаем x = 9.
-
- Пример 3: В пропорции a/b = 10/15, если a = 4, найти значение b.
Решение: Мы можем умножить 4 на 15 и поделить на 10, чтобы найти значение b. Получаем b = 6.
Пропорции используются в различных сферах жизни, таких как финансы, строительство и техника. Они помогают сравнивать и анализировать величины, а также решать разнообразные задачи.
Пример 1: Расчет площади прямоугольника
Площадь прямоугольника вычисляется по формуле:
S = a * b
где a — длина прямоугольника, а b — ширина прямоугольника.
Для примера рассмотрим прямоугольник, у которого длина равна 5 см, а ширина равна 3 см.
Применяя формулу, получим:
S = 5 * 3 = 15
Таким образом, площадь прямоугольника равна 15 см².
Пример 2: Расчет времени пути
Рассмотрим пример, в котором мы должны посчитать время, которое займет путь, пройденный автомобилем. Допустим, что автомобиль движется со скоростью 60 км/ч и должен преодолеть расстояние 120 км.
Для решения этой задачи мы можем использовать пропорцию. Пропорция — это равенство двух отношений. В данном случае, мы можем сформулировать пропорцию следующим образом:
Время / Расстояние = Скорость / Время
Давайте запишем известные нам значения в эту пропорцию:
Время / 120 км = 60 км/ч / Время
Мы хотим найти значение времени, поэтому переставим неизвестное значение Время в числителе:
Время = (60 км/ч * 120 км) / 1
Теперь, произведем вычисления:
Время = 7200 км * ч / 1
Итак, время, которое займет путь, равно 7200 часов.
Таким образом, автомобиль будет двигаться в течение 7200 часов, чтобы преодолеть расстояние 120 км со скоростью 60 км/ч.
Практическое применение пропорций
Пропорции используются во многих областях, таких как строительство, физика, экономика, медицина и т.д. Рассмотрим несколько примеров практического применения пропорций:
ОбластьПример применения
| Строительство | Расчет пропорций для построения прочных и устойчивых конструкций |
| Финансы | Вычисление процентных ставок и расчет доходности инвестиций |
| Кулинария | Подбор пропорций ингредиентов для приготовления рецептов |
| Медицина | Определение дозировки лекарств и расчет пропорций смесей для медицинских процедур |
В каждом из этих примеров пропорции позволяют нам установить соотношение между различными величинами и использовать это соотношение для решения практических задач. Изучение пропорций в математике помогает нам развить навыки логического мышления и аналитического решения задач.
Строительство
В строительстве используются пропорции для определения длин, площадей и объемов. Например, при планировке помещений в здании необходимо учитывать пропорции, чтобы обеспечить комфортное пространство и функциональность.
Также пропорции применяются при проектировании фундаментов, стен, крыш и других конструкций. Они помогают определить необходимые размеры и распределение материалов для обеспечения прочности и безопасности здания.
Пропорции также применяются при расчете стоимости строительства. Путем установления соотношения между стоимостью материалов и объемом работ можно определить общую стоимость проекта и его бюджет.
Важно учитывать, что пропорции в строительстве могут быть не только линейными, но и площадными и объемными. Они определяются требованиями проекта и спецификой конкретной задачи.
Примеры пропорций в строительстве:
| Соотношение высоты стены к ее ширине |
| Размеры окон относительно размеров помещения |
| Площадь пола относительно высоты потолка |
| Объем фундамента относительно массы здания |
Финансы
Основными принципами финансов являются:
- Разделение доходов на потребление, накопление и инвестирование.
- Управление рисками и финансовой безопасностью.
- Приоритизация и планирование расходов.
- Определение и достижение финансовых целей.
Пропорции в математике также имеют применение в финансах. Например, при расчете процентов по кредиту или вкладу используются пропорции. Также финансовые отчеты могут содержать информацию о соотношении различных показателей, которое также может быть выражено в виде пропорции.
Изучение финансов помогает людям принимать разумные финансовые решения и достигать финансовой независимости. Оно также важно для бизнеса, государственного управления и других организаций.


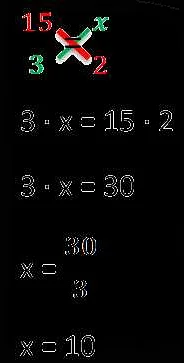


Статья очень понятно и доступно объяснила основные понятия пропорций в математике для 7 класса. Я, как читатель, была приятно удивлена, насколько просто и наглядно автор изложил материал. Теперь я легко могу разобраться с такими понятиями, как пропорциональность, прямая и обратная пропорции. Было очень полезно узнать, что пропорции широко используются в реальной жизни, например, при решении задач на смешивание веществ или при расчете времени. Я также оценила примеры, которые автор привел в статье. Они помогли мне лучше понять, как применять пропорции на практике. В целом, статья оказалась очень полезной и информативной, и я надеюсь, что автор продолжит делиться такими интересными материалами.