Сколько всего концертов в математике

Узнайте сколько всего существует концертов в математике: перестановки, комбинации и размещения. Изучите особенности каждого типа и применение в решении задач.

Математика – это наука, которая изучает стройность и определенность. Она является фундаментальной дисциплиной и имеет множество различных областей применения. Одной из таких областей является теория множеств и комбинаторика, в которой вводится понятие «концерты».

Концерты в математике — это упорядоченные наборы элементов из множества, которые имеют определенные свойства и правила. В зависимости от этих свойств и правил, концерты могут быть разных видов и иметь различные названия.

Например, одним из наиболее известных видов концертов является перестановка. Перестановка — это упорядоченный набор элементов, в котором каждый элемент встречается только один раз. Например, перестановкой из трех элементов A, B и C может быть ABC, BAC, CAB и т.д.

Также существуют концерты с ограничениями, например, комбинаторные числа или сочетания. Комбинаторные числа определяют количество различных способов выбрать k элементов из множества размером n без учета порядка. Например, количество сочетаний из трех элементов A, B и C без учета порядка будет равно 3.

Сколько всего концертов в математике?

Вот некоторые из них:

1. Граф концерта: математический объект, представляющий собой набор вершин и ребер, используемых для моделирования связей между объектами.
2. Концертные алгоритмы: математические алгоритмы, используемые для решения различных задач в концертной теории.
3. Концертные системы: набор объектов и операций, образующих структуру, в которой можно выполнять определенные операции или свойства.
4. Теория концертов: научная дисциплина, изучающая свойства и взаимосвязи между концертами и другими математическими объектами.

Это лишь некоторые примеры концертов в математике. Каждый из них имеет свои особенности и применения в различных областях математики и ее приложениях. Изучение концертов позволяет лучше понять структуры и отношения в различных математических системах и применить полученные знания в решении задач и проблем.

Определение и классификация концертов.

Концерты можно классифицировать по различным критериям:

По жанру:

• Классический концерт — исполнение произведений классической музыки, как оркестровых, так и сольных;
• Рок-концерт — выступления рок-групп и исполнителей рок-музыки;
• Джазовый концерт — исполнение произведений джазовой музыки, как инструментальной, так и вокальной;
• Поп-концерт — выступления популярных исполнителей и групп, исполняющих поп-музыку;
• Этнический концерт — исполнение произведений народной и этнической музыки разных стран и культур.

По масштабу:

• Массовый концерт — организация выступления большого количества исполнителей перед большой аудиторией;
• Интимный концерт — маленькое выступление перед небольшой группой людей, как правило, в небольших помещениях;
• Фестиваль — организация нескольких концертов на одной площадке в течение определенного периода времени.

Концерты являются популярной формой развлечения и культурного события. Они позволяют людям наслаждаться музыкой и искусством, создают атмосферу взаимодействия и эмоционального переживания. Независимо от жанра или масштаба, концерты оставляют яркое впечатление и позволяют исполнителям и аудитории наслаждаться музыкой вместе.

Концерты первого рода и их особенности.

Концерты первого рода, также известные как концерты с одним зрителем, являются наиболее простым типом концертов. В них участвует только один исполнитель и один зритель. Такой концерт можно представить себе как диалог между исполнителем и зрителем.

Особенностью концертов первого рода является то, что они могут быть представлены в виде графов. Граф представляет собой набор вершин (исполнителей и зрителей) и ребер, которые связывают эти вершины. В случае концертов первого рода граф будет состоять из двух вершин и одного ребра, соединяющего эти вершины.

Еще одной особенностью концертов первого рода является то, что они могут быть оформлены в виде таблицы. В таблице каждая строка представляет собой один концерт, а столбцы содержат информацию о исполнителе и зрителе.

Концерты первого рода являются фундаментальным понятием в теории графов и имеют множество применений в различных областях математики и информатики. Изучение и анализ концертов первого рода позволяет лучше понять основы теории графов и развивать навыки анализа и моделирования.

Концерты второго рода и их разновидности.

Существует несколько разновидностей концертов второго рода, включая:

1. Перестановки. В этом случае все элементы множества участвуют в комбинации, и каждый элемент может быть использован только один раз. Порядок элементов важен.
2. Размещения. Здесь также учитывается порядок элементов, но каждый элемент может быть использован несколько раз.
3. Сочетания. В отличие от перестановок, в сочетаниях порядок элементов не имеет значения. Каждый элемент может быть использован только один раз.
4. Мультимножества. В мультимножествах элементы могут повторяться, и порядок их следования важен.

Концерты второго рода находят свое применение в различных областях математики, физики и информатики. Они широко используются для решения задач по комбинаторике, криптографии, анализу алгоритмов и других областей.

Концерты третьего рода и их применение.

В концертах третьего рода участвуют несколько музыкантов, которые играют на разных инструментах. Каждый музыкант должен исполнить свой собственный музыкальный фрагмент, а затем все музыканты должны сыграть вместе какую-то общую музыкальную фразу. При этом нужно соблюдать определенные условия и правила.

Концерты третьего рода широко применяются в различных областях математики и информатики. Они используются для решения задач комбинаторики, теории вероятностей, теории игр и других областей. Эти концерты помогают исследовать различные комбинаторные структуры и развивать алгоритмическое мышление.

В таблице ниже приведены некоторые примеры концертов третьего рода и их применение:

Название концертаПрименение

Концерт Штольца	Исследование комбинаторных структур в теории вероятностей
Концерт Дирехле	Алгоритмическое решение задач комбинаторики
Концерт Эйлера	Изучение теории игр и оптимальных стратегий

Концерты третьего рода являются важным инструментом для анализа и изучения комбинаторных структур. Они помогают развивать логическое мышление и способствуют решению сложных задач в различных областях математики и информатики.

Концерты четвертого рода и их свойства.

Концерты четвертого рода в математике представляют собой особый вид сочетаний или перестановок элементов. В отличие от концертов первого, второго и третьего рода, концерты четвертого рода имеют свои уникальные свойства и особенности.

Основное свойство концертов четвертого рода заключается в том, что они представляют собой перестановки элементов в которых все элементы различны, и каждый элемент занимает свою уникальную позицию. Другими словами, в концертах четвертого рода нет повторяющихся элементов и каждый элемент имеет свой уникальный номер.

Концерты четвертого рода широко применяются в комбинаторике и теории вероятностей. Они позволяют решать различные задачи, связанные с определением числа возможных вариантов перестановок элементов и расчетом вероятностей событий.

Для определения числа концертов четвертого рода используется формула перестановок. Если имеется набор из n элементов, то число концертов четвертого рода равно n! (n факториал).

Пример: если имеется набор из 5 элементов, то число концертов четвертого рода равно 5! = 5 * 4 * 3 * 2 * 1 = 120.

Концерты четвертого рода являются важным инструментом для анализа и решения различных задач в математике. Их свойства и особенности позволяют эффективно и точно решать задачи, связанные с перестановками элементов и расчетом вероятностей.

Концерты пятого рода и их примеры.

Примеры концертов пятого рода:

1. Концерт Фибоначчи — в этом концерте музыкальная структура основана на последовательности чисел Фибоначчи. Каждая нота соответствует числу Фибоначчи, и музыкальная линия строится на основе этих чисел.
2. Концерт Пи — в этом концерте музыкальная структура основана на числе Пи. Каждая нота соответствует цифре числа Пи, и музыкальная линия строится на основе этих цифр.
3. Концерт Хаусдорфа — в этом концерте музыкальная структура основана на множестве Хаусдорфа. Каждая нота соответствует элементу множества Хаусдорфа, и музыкальная линия строится на основе этих элементов.

Это лишь некоторые примеры концертов пятого рода, и в реальности их разнообразие намного шире. Концерты пятого рода являются уникальным способом объединения математики и музыки, позволяющим увидеть и услышать математические закономерности в музыкальных произведениях.

Концерты шестого рода и их роль в математике.

Основной идеей концертов шестого рода является использование операций сложения, вычитания, умножения и деления для получения определенного числового результата. В отличие от других видов концертов, где используются только две операции, в концертах шестого рода применяются все четыре основные арифметические операции.

Концерты шестого рода имеют множество разновидностей и применяются в различных областях математики. Они помогают решать задачи в алгебре, геометрии, теории вероятностей и других разделах математики. Кроме того, они играют важную роль в развитии логического мышления и аналитических навыков.

Для удобства выполнения концертов шестого рода используется таблица, в которой числа и операции располагаются в определенном порядке. Такая таблица помогает систематизировать информацию и упрощает процесс решения задач.

В заключение, концерты шестого рода представляют собой важный инструмент в математике, который помогает исследователям и ученым находить новые закономерности, решать сложные задачи и разрабатывать новые подходы к решению математических проблем. Их использование способствует развитию математического мышления и обогащению знаний в области математики.

ОперацияПример

Сложение	2 + 3 = 5
Вычитание	5 — 2 = 3
Умножение	2 * 3 = 6
Деление	6 / 3 = 2

Вопрос-ответ:

Какое количество концертов существует в математике?

В математике существует бесконечное количество различных концертов.

Можете ли вы назвать некоторые разновидности концертов в математике?

Некоторые разновидности концертов в математике включают концерты вероятности, концерты теории чисел, концерты геометрии и концерты алгебры, чтобы назвать только некоторые.

Какие основные различия между разными видами концертов в математике?

Основные различия между разными видами концертов в математике обычно связаны с предметной областью, которой они занимаются. Например, концерты вероятности изучают вероятностные модели и статистику, в то время как концерты теории чисел изучают свойства целых чисел.

Какой вид концертов в математике наиболее популярен?

Нет одного конкретного вида концертов, который можно назвать наиболее популярным, так как предпочтения людей в математике могут различаться. Однако некоторые области, такие как алгебра и геометрия, являются основными компонентами математического образования и исследований.

Какие применения имеют концерты в математике в реальном мире?

Концерты в математике имеют множество применений в реальном мире. Например, концерты вероятности используются для анализа данных и прогнозирования событий, концерты геометрии применяются в архитектуре и дизайне, а концерты алгебры используются для решения задач в финансах и компьютерных науках, чтобы назвать только некоторые.

Сколько всего различных видов концертов существует в математике?

В математике существует бесконечное количество различных видов концертов. Концерты в математике могут быть разного типа и характера, включая концерты функций, концерты чисел, концерты графов и многое другое. Каждый вид концерта имеет свои особенности и применения в математических исследованиях и задачах.

Какие разновидности концертов в математике наиболее распространены?

В математике наиболее распространены различные виды концертов функций. Это может быть концерт графика функции, где на оси координат строятся точки и структуры, представляющие функцию. Также популярны концерты функциональных уравнений, где исследуются свойства и решения уравнений с использованием методов аналитической геометрии и алгебры. Кроме того, существуют концерты комбинаторики, где изучаются различные комбинаторные структуры и их свойства.

Сравнение различных видов концертов и их применение в практике.

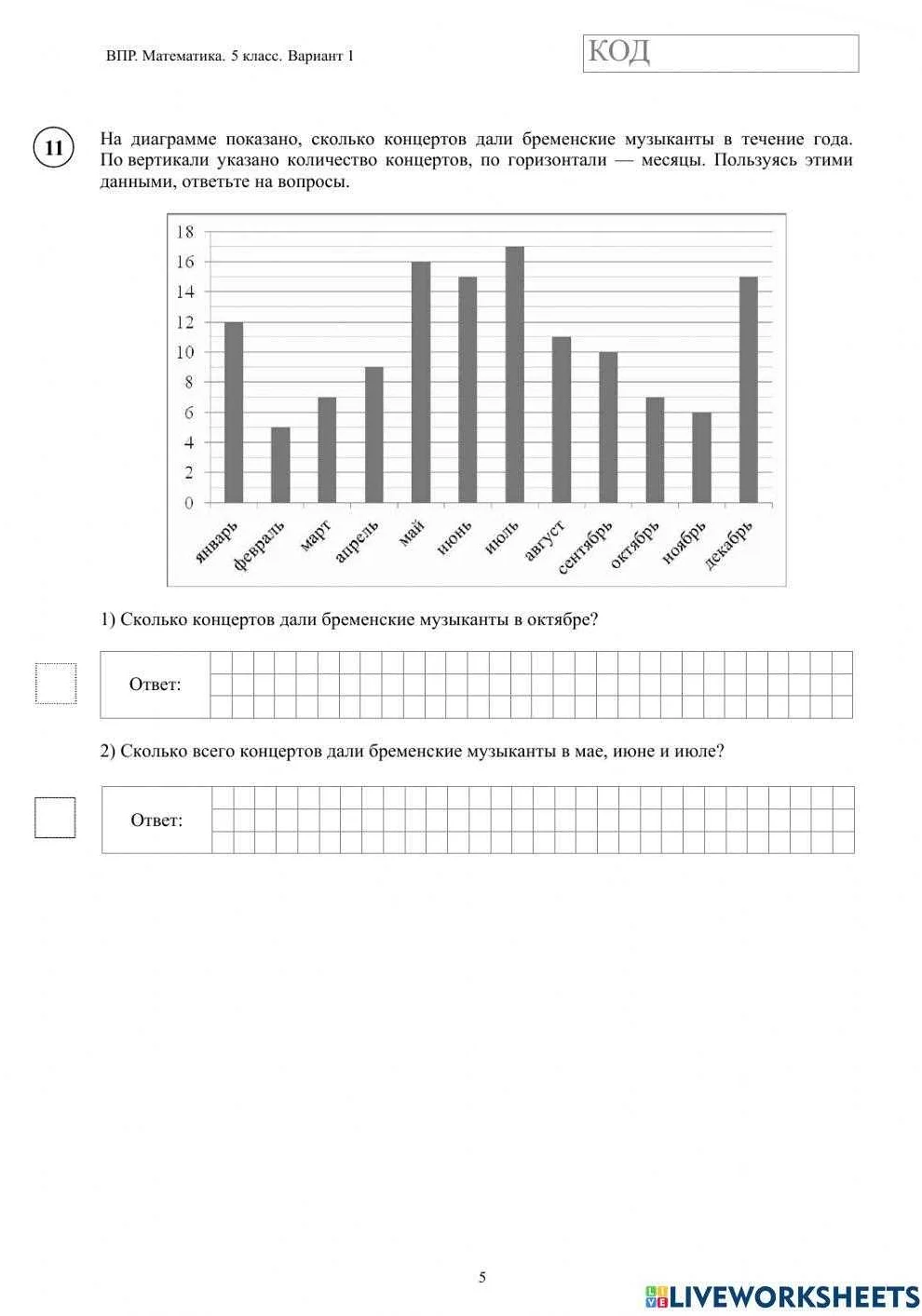
В мире математики существует несколько различных видов концертов, каждый из которых имеет свои особенности и применение в практике. Рассмотрим некоторые из них.

Первый вид концерта — концерт симметрии. В этом концерте акцент делается на симметричных свойствах фигур и объектов. Он помогает учащимся развить навыки анализа и различения симметричных и несимметричных форм. Также концерт симметрии может иметь практическое применение в дизайне, графике и архитектуре.

Второй вид концерта — концерт вероятности. В этом концерте рассматриваются вероятности событий и их влияние на результаты экспериментов. Участники концерта учатся оценивать вероятности различных исходов и делать выводы на основе этих вероятностей. Концерт вероятности имеет практическое применение в статистике, финансах, играх на удачу и принятии решений.

Третий вид концерта — концерт чисел. В этом концерте учащиеся знакомятся с различными группами чисел, их свойствами и операциями над ними. Они изучают арифметические операции, алгебру, геометрию и другие разделы математики. Концерт чисел помогает развить аналитическое мышление и навыки решения математических задач. Он также имеет практическое применение в финансовой сфере, науке, технике и многих других областях.

И наконец, четвертый вид концерта — концерт матриц. В этом концерте рассматриваются матрицы и их применение в различных областях. Участники концерта изучают операции над матрицами, их свойства и применение в линейной алгебре, графиках, физике и других науках. Концерт матриц помогает развить навыки абстрактного мышления и решения сложных задач.

Таким образом, различные виды концертов в математике имеют свои особенности и применение в практике. Они помогают учащимся развить различные навыки и знания, которые могут быть полезными в различных областях жизни.

Видео по теме: