Что такое тетраэдра в математике

Тетраэдр — это геометрическое тело, состоящее из четырех треугольных граней. В математике тетраэдр является одним из основных полиэдров и имеет множество интересных свойств и приложений. Узнайте, какие особенности и применения имеет тетраэдр в математике.

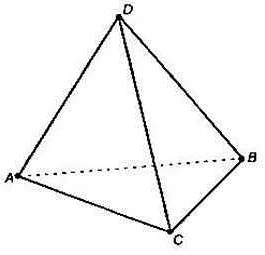
Тетраэдр — одна из основных фигур в геометрии, которая является трехмерным полиэдром. Тетраэдр состоит из четырех треугольных граней, шести ребер и четырех вершин. Каждая вершина тетраэдра соединена с каждой вершиной по ребру, и все ребра тетраэдра имеют одинаковую длину. Тетраэдр является примером правильного полиэдра, у которого все грани равны и все углы между гранями являются прямыми углами.

Тетраэдр имеет несколько важных свойств. Во-первых, сумма углов всех граней тетраэдра равна 360 градусам. Во-вторых, тетраэдр является пирамидой, у которой основание представляет собой треугольник. Также, тетраэдр обладает симметрией относительно своих граней, ребер и вершин.

Примеры тетраэдра можно найти в различных областях науки и техники. Например, в химии тетраэдр используется для обозначения молекулы с четырьмя атомами, связанными между собой. В графическом моделировании тетраэдр часто используется в качестве основы для создания трехмерных моделей объектов. Тетраэдры также применяются в математической теории игр, топологии и геодезии.

Что такое тетраэдр?

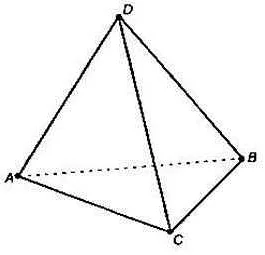
Каждая грань тетраэдра является равносторонним треугольником, то есть все ее стороны и углы равны между собой. Ребра тетраэдра соединяют вершины и определяют его форму. Все ребра тетраэдра имеют одинаковую длину.

Тетраэдр обладает несколькими важными свойствами. Один из них — это связь между единичным тетраэдром и октаэдром. Октаэдр может быть разбит на восемь равных тетраэдров, а единичный тетраэдр может быть объединен с семью другими такими же тетраэдрами, чтобы образовать октаэдр.

Тетраэдры могут встречаться в различных областях математики и физики. Они используются для моделирования молекул, кристаллических структур, графиков и других объектов. Тетраэдр также имеет множество интересных свойств, которые исследуются математиками.

Основные свойства тетраэдра

1. Число граней: тетраэдр имеет 4 грани.
2. Число вершин: тетраэдр имеет 4 вершины.
3. Число ребер: тетраэдр имеет 6 ребер.
4. Равные грани: все грани тетраэдра являются равнобедренными треугольниками.
5. Плоскость: все грани тетраэдра лежат в одной плоскости.
6. Выпуклость: тетраэдр является выпуклым телом, то есть все его вершины лежат в одной стороне от каждой плоскости грани.
7. Объем: объем тетраэдра можно вычислить по формуле V = (1/6) * A * h, где A — площадь основания, h — высота, опущенная из вершины тетраэдра на основание.
8. Площадь поверхности: площадь поверхности тетраэдра можно вычислить суммируя площади всех его граней.

Это лишь некоторые из основных свойств тетраэдра. Это уникальное геометрическое тело имеет множество других интересных математических свойств и применений в различных областях науки и техники.

Формула объема тетраэдра

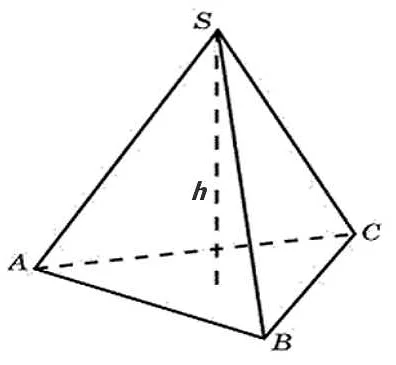
Формула для вычисления объема тетраэдра выглядит следующим образом:

V = (1/3) * S * h,

где V — объем тетраэдра, S — площадь одной из его граней, h — высота, опущенная из вершины тетраэдра на основание.

Для вычисления объема тетраэдра, необходимо знать площадь одной из его граней и длину высоты. Площадь грани можно вычислить с использованием формулы для площади треугольника, например, с помощью формулы Герона. Длину высоты можно определить с использованием теоремы Пифагора или других методов в зависимости от известных данных о тетраэдре.

Приведем пример расчета объема тетраэдра. Пусть площадь грани равна 10 квадратных единиц, а высота равна 5 единиц. Тогда объем тетраэдра будет равен:

V = (1/3) * 10 * 5 = 50/3 ≈ 16.67 кубических единиц.

Таким образом, формула для вычисления объема тетраэдра позволяет определить объем этого геометрического тела на основе известных данных о его гранях и высоте. Эта формула является основной для решения задач, связанных с тетраэдрами в математике.

Тетраэдр и его грани

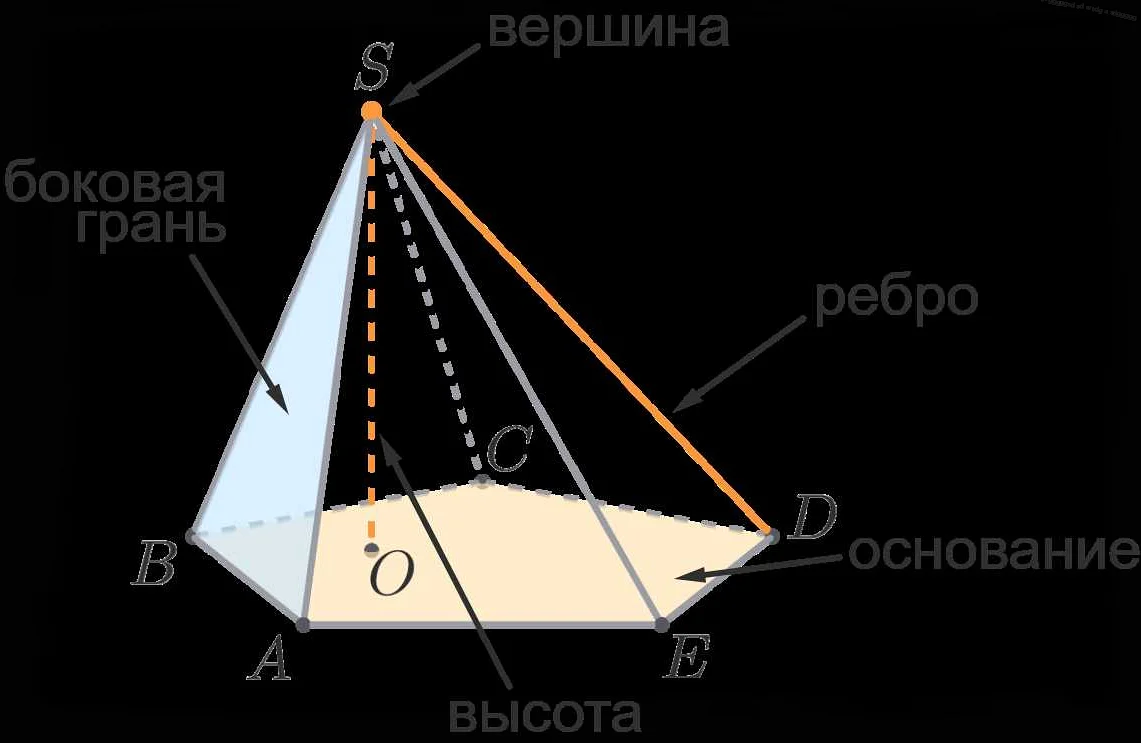
Грани тетраэдра — это треугольники, которые образуют его поверхность. Всего у тетраэдра есть четыре грани. Каждая грань состоит из трех ребер, которые также называются сторонами грани.

Тетраэдр обладает несколькими важными свойствами, связанными с его гранями. Например, сумма площадей всех граней тетраэдра равна площади его поверхности. Кроме того, сумма длин всех ребер тетраэдра равна периметру его граней.

Одна из особенностей тетраэдра — его грани являются плоскими фигурами, что отличает его от других многогранников, таких как куб или икосаэдр.

Примеры тетраэдров можно найти в различных областях, включая химию, физику и геометрию. Например, в химии тетраэдр может представлять молекулу метана (CH4), а в физике — кристаллическую структуру некоторых материалов.

Тетраэдр и его вершины

У тетраэдра есть четыре вершины, которые образуют его основу. Каждая вершина тетраэдра соединяется с каждой другой вершиной линией, образуя четыре ребра. Также есть шесть ребер, каждое из которых соединяет две вершины тетраэдра.

Тетраэдр имеет три оси симметрии, которые проходят через вершины и центр масс тетраэдра. Эти оси деляют тетраэдр на четыре равных треугольника, которые являются его гранями.

Примеры тетраэдра в реальной жизни включают пирамиду и ромб. Тетраэдр также является одной из платонических тел, которые имеют определенные свойства и симметрию.

Вершины тетраэдра можно определить с помощью координат. Обозначим вершины тетраэдра как A, B, C и D. Тогда координаты каждой вершины можно представить в виде (x, y, z), где x, y и z — это координаты точки в трехмерном пространстве. Например, вершина A может иметь координаты (x1, y1, z1), вершина B — (x2, y2, z2), и так далее.

Тетраэдр и его вершины играют важную роль в геометрии и многих других областях науки. Изучение и понимание свойств и структуры тетраэдра помогают нам лучше понять трехмерное пространство и его взаимосвязи с математикой и физикой.

Тетраэдр в пространстве

Тетраэдр в пространстве можно представить как пирамиду с треугольным основанием и точкой, которая является вершиной пирамиды. Каждая грань тетраэдра является треугольником, а каждая вершина соединяется с каждой другой вершиной ребром.

Тетраэдр в пространстве обладает следующими свойствами:

• Число вершин: тетраэдр имеет четыре вершины;
• Число ребер: тетраэдр имеет шесть ребер;
• Число граней: тетраэдр имеет четыре грани;
• Высота: тетраэдр имеет высоту, которая является перпендикулярной линией, спускающейся с вершины тетраэдра к плоскости основания;
• Объем: объем тетраэдра вычисляется по формуле: V = (a^3 * sqrt(2)) / 12, где a — длина ребра тетраэдра.

Примеры тетраэдров в пространстве встречаются в различных областях науки и техники. Например, тетраэдры используются в моделировании молекул, в архитектуре и в компьютерной графике.

Видео по теме:

Вопрос-ответ:

Что такое тетраэдр?

Тетраэдр — это геометрическое тело, состоящее из четырех треугольных граней, которые пересекаются по общим ребрам.

Как можно найти площадь поверхности тетраэдра?

Площадь поверхности тетраэдра можно найти суммируя площади его граней.

Какие свойства у тетраэдра?

У тетраэдра есть несколько свойств, включая: каждая грань тетраэдра является треугольником, все грани пересекаются по общим ребрам, каждое ребро имеет ровно две грани и каждый угол между гранями равен 60 градусам.

Как найти объем тетраэдра?

Объем тетраэдра можно найти, используя формулу: V = (1/6) * S * h, где S — площадь основания тетраэдра, а h — высота, опущенная из вершины на основание.

Можете привести примеры реальных объектов, которые имеют форму тетраэдра?

Некоторые примеры реальных объектов, которые имеют форму тетраэдра, включают пирамидки, ромбоэдры, а также некоторые кристаллы и молекулы.

Что такое тетраэдр в математике?

Тетраэдр — это геометрическое тело, состоящее из четырех треугольных граней, которые пересекаются по общим ребрам.

Примеры тетраэдров в природе

Кристаллы Тетраэдральная форма может быть наблюдаема во многих кристаллах. Например, пирит (FeS2) и гексагональный кварц (SiO2) имеют тетраэдральную структуру.	Снежинки Некоторые снежинки имеют тетраэдральную форму. Это связано с особенностями кристаллизации льда в атмосфере.
Пчелиные соты Пчелиные соты имеют тетраэдральную форму, которая обеспечивает максимальную прочность и экономию материала.	Молекулы Некоторые молекулы могут иметь тетраэдральную форму. Например, метан (CH4) имеет тетраэдральную структуру, где атом углерода находится в центре, а четыре атома водорода расположены по углам тетраэдра.

Это лишь несколько примеров, и на самом деле тетраэдры можно обнаружить во многих других объектах и структурах в природе. Изучение этих примеров помогает нам лучше понять и использовать концепцию тетраэдра в математике и других научных областях.

Практическое применение тетраэдров

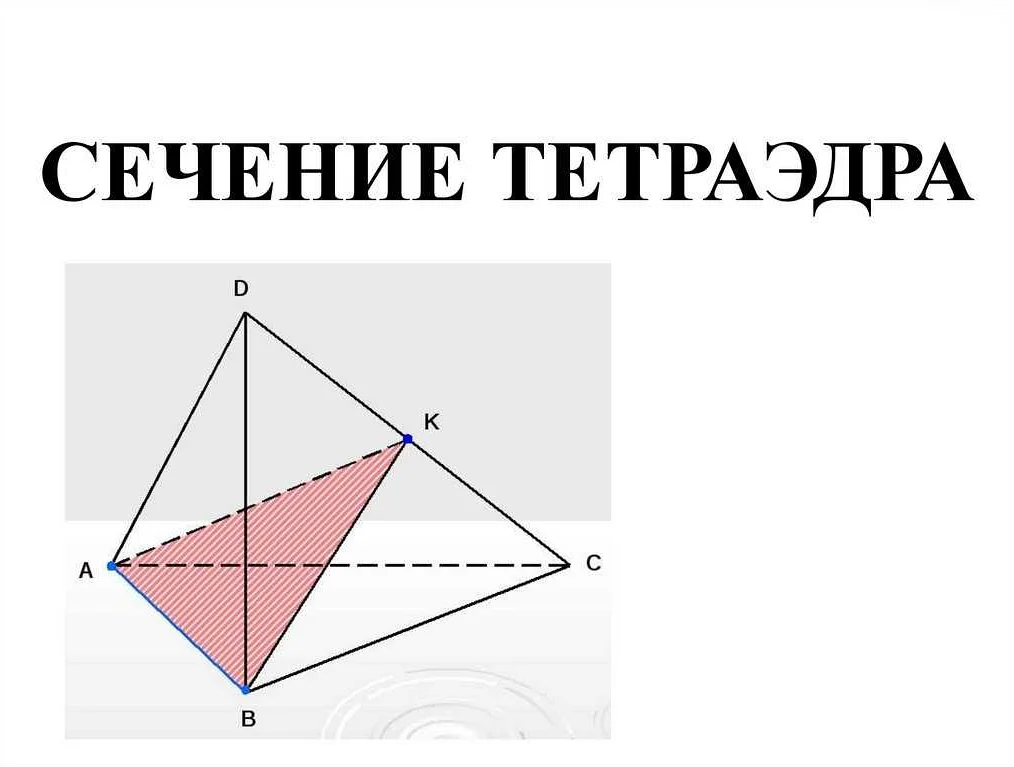
Тетраэдр, как геометрическая фигура, находит свое применение в разных областях науки и техники. Его особенности и свойства позволяют использовать его в различных задачах и конструкциях.

Одно из практических применений тетраэдров — в геодезии и картографии. Тетраэдры используются для разбиения пространства на неравные части и создания сеток, которые помогают визуализировать и анализировать географические данные.

Тетраэдры также применяются в физике и химии. В кристаллографии тетраэдры используются для описания структуры кристаллов и определения их свойств. Они помогают ученым изучать связи между атомами и молекулами в кристаллической решетке.

В строительстве и архитектуре тетраэдры находят применение в создании устойчивых и прочных конструкций. Тетраэдрические формы могут быть использованы в каркасах зданий, мостов и других инженерных сооружений.

Тетраэдр также используется в компьютерной графике и моделировании. Он может быть использован для создания трехмерных моделей и анимаций, а также для расчетов визуальных эффектов и симуляций.

Таким образом, тетраэдр имеет широкий спектр применения в различных областях науки и техники. Его геометрические свойства делают его полезным инструментом для решения различных задач и создания новых конструкций и моделей.