Что значит штрих в математике

Штрих в математике — это символ, используемый для обозначения различных величин или операций. Узнайте, как использовать штрих в различных математических контекстах и как он может помочь вам в решении задач.

В математике штрих – важный символ, который используется для обозначения различных понятий и операций. Штрих может применяться к числам, функциям, переменным и другим математическим объектам. Он часто используется для указания производной функции, а также для обозначения обратной функции или обратного числа.

Производная функции представляет собой меру изменения функции в каждой точке её области определения. Обозначение производной с помощью штриха было предложено Леонардом Эйлером в XVIII веке. Например, если у нас есть функция y = f(x), то производная этой функции обозначается как y’ или f'(x). Штрих может быть также использован для обозначения нескольких производных, например, y» для второй производной и так далее.

Штрих также может использоваться для обозначения обратной функции или обратного числа. Обратная функция f^(-1)(x) обозначается с помощью штриха над функцией, то есть f^(-1)'(x). Аналогично, обратное число a^(-1) может быть обозначено как a’.

Штрих – это мощный символ, который позволяет упростить запись математических формул и обозначить важные концепции. Он используется для обозначения производной функции, обратной функции и обратного числа. Понимание значения штриха в математике поможет лучше разобраться в производных, обратных функциях и других важных понятиях.

История штриха в математике

Первоначально штрих использовался только для обозначения производной функции. Эта идея была разработана немецким математиком Лайбницем в конце 17 века. Лайбниц предложил использовать символ штриха как способ обозначения производной, чтобы отличить его от других обозначений, которые использовались в то время.

С течением времени штрих стал широко использоваться и в других областях математики. Например, он используется для обозначения производной функции по переменной времени в дифференциальных уравнениях. Также штрих может обозначать разделение чисел или символов, а также операцию дифференцирования в других областях математики.

Штрих является важным и удобным математическим символом, который используется во многих различных областях математики. Он помогает обозначить различные операции и производные, что делает математические выражения более понятными и удобными в использовании.

Понятие штриха в математике

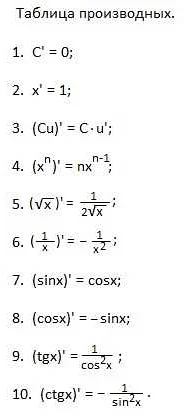
В математике штрих используется для обозначения различных величин и операций. Он может иметь разные значения, в зависимости от контекста.

• Штрих над буквой обычно обозначает производную функции по переменной. Например, если функция обозначается символом f(x), то ее производная будет обозначаться как f'(x) или f(x)’.
• Штрих под буквой может указывать на обратную функцию. Например, если функция обозначается символом f(x), то обратная функция будет обозначаться как f-1(x).
• Двойной штрих над буквой может обозначать вторую производную функции. Например, f»(x) означает вторую производную функции f(x).
• Штрих после математического выражения может указывать на дифференцирование по времени. Например, если x — функция времени, то x’ будет обозначать производную этой функции по времени.

Штрих также может использоваться для обозначения других математических операций или отношений, в зависимости от конкретной задачи или области математики.

Основные операции с штрихом

В математике штрих используется для обозначения различных операций и преобразований. Рассмотрим основные из них:

1. Производная – это основная операция, для которой штрих широко используется. В математическом анализе производная функции обозначается символом f'(x) или \(\frac{{dy}}{{dx}}\), где x – переменная, а y – функция, производную которой необходимо найти. Производная позволяет определить скорость изменения функции в зависимости от значения аргумента.
2. Первообразная – это обратное преобразование к производной. Первообразная функции f(x) обозначается символом F(x) и определяется условием, что F'(x) = f(x). Таким образом, первообразная позволяет найти функцию, производная которой равна заданной функции.
3. Краткое дифференцирование – это операция, при которой штрих ставится непосредственно после функции. Например, если f(x) = x^2 + 3x, то f'(x) = 2x + 3.
4. Высокий штрих – это операция, позволяющая обозначить n-ю производную функции. Для обозначения n-й производной используется символ f^(n)(x) или \(\frac{{d^n}}{{dx^n}}\), где n – неотрицательное целое число.
5. Комбинированные операции – штрих может использоваться вместе с другими математическими операциями. Например, в математическом анализе штрих часто ставится после знака суммы или интеграла, чтобы обозначить операцию дифференцирования или интегрирования.

Таким образом, штрих является важным математическим символом, который позволяет обозначить различные операции и преобразования в математике.

Геометрическое значение штриха

Главным образом, штрих используется для обозначения параллельных линий или отрезков. Например, штрих может быть проведен над двумя линиями, чтобы показать, что они параллельны. Также штрих может быть проведен над отрезком, чтобы указать, что он равен другому отрезку.

Штрихи также используются для обозначения углов. Например, штрих может быть проведен над двумя лучами, чтобы показать, что они образуют вертикальные углы. Также штрих может быть проведен над углом, чтобы указать его меру в градусах.

Геометрическое значение штриха может быть разным в разных контекстах. Однако во всех случаях штрих играет важную роль в обозначении и описании геометрических объектов и их свойств.

Примеры использования штриха в математике

1. Штрих над буквой

Штрих может быть поставлен над буквой, чтобы указать на производную. Например, если функция f(x) имеет производную f'(x), то штрих над буквой f обозначает эту производную. Таким образом, f'(x) читается как «эф штрих» или «эф-при-экс».

2. Двойной штрих над буквой

Двойной штрих над буквой обозначает вторую производную функции. Например, функция f(x) может иметь первую производную f'(x) и вторую производную f»(x). Таким образом, f»(x) читается как «эф двойной штрих» или «эф-двойное-при-экс».

3. Штрих вокруг буквы или символа

Штрих может быть поставлен вокруг буквы или символа для обозначения комплексного сопряжения. Например, если z – комплексное число, то z’ обозначает его комплексно-сопряженное число.

4. Штрих над знаком функции

Штрих может быть поставлен над знаком функции для обозначения обратной функции. Например, если f(x) – функция, то f^(-1)(x) обозначает ее обратную функцию.

5. Штрих в матрицах

Штрих может быть использован в матрицах для обозначения транспонирования. Например, если A – матрица, то A’ обозначает транспонированную матрицу А.

Это лишь некоторые примеры использования штриха в математике. Штрих имеет и другие значения и применения в различных областях математики, таких как дифференциальное исчисление, теория вероятностей, теория множеств и др.

Штрих как инструмент в доказательствах

Один из основных способов применения штриха в доказательствах — это применение алгебраических преобразований. Например, если нужно доказать равенство двух выражений, можно применить различные алгебраические операции, такие как раскрытие скобок, сокращение подобных членов и перестановка слагаемых. При каждом преобразовании используется штрих, чтобы указать, что равенство остается справедливым.

Штрих также применяется при доказательствах неравенств. Например, чтобы доказать, что одно выражение больше другого, можно применить различные операции сравнения, такие как сложение и умножение на положительное число. При каждой операции используется штрих, чтобы указать, что неравенство сохраняется.

Кроме того, штрих используется для обозначения производной функции. Например, если нужно найти производную функции, то обычно используется обозначение f'(x) или df/dx, где штрих указывает на производную по переменной x.

Таким образом, штрих является неотъемлемым инструментом в математике, который помогает проводить различные операции и преобразования при доказательствах. Он позволяет ясно указывать на шаги доказательства и делает математические выкладки более понятными и четкими.

Штрих и символы математической нотации

Одним из распространенных использований штриха является обозначение производной функции. Если функция обозначается символом f(x), то производная этой функции обозначается символом f'(x). Штрих в этом случае указывает на операцию дифференцирования и показывает, что мы берем производную функции по переменной x.

Штрих может также использоваться для обозначения различных операций и преобразований. Например, в матричной алгебре штрих используется для обозначения транспонирования матрицы. Если матрица обозначается символом A, то транспонированная матрица обозначается символом A’. Также штрих может использоваться для обозначения сопряженного числа, обратного числа и других математических операций.

В некоторых случаях штрих может также обозначать производные и отношения, которые являются производными. Например, в физике штрих может использоваться для обозначения производной по времени. Также штрих может обозначать различные производные, такие как производная по пространственным координатам или производная по другим переменным.

Штрих является важным символом в математической нотации и его использование помогает уточнить и обозначить различные математические понятия. Знание основных значений и применений штриха позволяет лучше понять и анализировать математические выражения и формулы.

Значение штриха в других областях науки

В физике штрих может обозначать производную по времени или по координате. Например, в уравнении движения штрих над переменной означает производную этой переменной по времени.

В химии штрих может обозначать различные степени окисления атомов в химических соединениях. Например, при обозначении формулы химического вещества штрих используется для указания степени окисления атома.

В экономике и финансах штрих может указывать на изменение какого-либо показателя или цены. Например, штрих над символом доллара может означать изменение курса валюты.

Таким образом, штрих имеет различное значение в разных областях науки и используется для обозначения различных понятий и явлений.

Вопрос-ответ:

Зачем в математике используется штрих?

Штрих в математике используется для обозначения различных операций и свойств чисел. Он помогает указать, что речь идет о нечто отличное от обычного числа.

Что означает штрих после числа?

Штрих после числа может иметь различные значения в зависимости от контекста. Например, в алгебре штрих после числа может обозначать операцию инверсии, или обратное число. В теории множеств штрих может указывать на комплементарность множества.

Как в математике обозначается обратное число?

Обратное число обычно обозначается с помощью штриха после числа. Например, обратное число для 5 будет обозначаться как 5′. Это число, при умножении на исходное число, дает результат 1.

В каких случаях используется штрих в теории множеств?

В теории множеств штрих используется для обозначения дополнительного множества. Например, если у нас есть множество A, то штрих после него обозначает дополнение этого множества, то есть все элементы, которые не принадлежат множеству A.

Каким образом штрих используется в геометрии?

В геометрии штрих может обозначать различные операции и свойства фигур. Например, в случае треугольника штрих может обозначать, что треугольник является подобным другому треугольнику. Также штрих может использоваться для обозначения отрезка или угла, которые имеют определенные свойства.

Что такое штрих в математике?

В математике штрих – это символ, который применяется для обозначения различных математических понятий, операций и преобразований. Он может иметь разные значения в разных областях математики.

Видео по теме: